Рангом матрицы называется наивысший порядок отличных от нуля миноров. Его обозначают через 
или 
.
СВОЙСТВА РАНГА МАТРИЦЫ
1. Ранг матрицы равен нулю только для нулевой матрицы. В других случаях ранг матрицы равен некоторому положительном числу.
2. Ранг прямоугольной матрицы не превышает меньшего из двух чисел 
и 
т.е. 
.
3. Для квадратной матрицы 
-го порядка 
только тогда, когда матрица невырожденная.
4. В случае квадратной матрицы если 
то определитель матрицы равен нулю.
При нахождении ранга матрицы, как правило, нужно вычислять большое количество определителей. Чтобы облегчить задачу студентам давным-давно найдены элементарные преобразования с помощью которых можно слегка поменяв вид матрицы без вычисления определителей посчитать ранг.
ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ МАТРИЦЫ
1. Транспонирование, т.е. замена каждой строки столбцом с тем же номером и наоборот.
2. Перестановка двух строк или двух столбцов.
3. Умножение всех элементов строки или столбца на любое число не равное нулю.
4. Добавление всех элементов строки или столбца соответствующих элементов параллельного ряда, умноженного на одно и то же число.
Матрицы, полученные одна из второй элементарными преобразованиями называются эквивалентными. Эквивалентные матрицы не равны друг другу, но при элементарных преобразованиях матрицы ее ранг не меняется. Если матрицы 
и 
эквивалентны то это записывается так: 
Рассмотрим два основных метода нахождения ранга матрицы.
Первый метод –- метод окантовки - заключается в следующем:
Если все миноры 1-го порядка, т.е. элементы матрицы равны нулю, то 
.
Если хоть один из миноров 1-го порядка не равен нулю, а все миноры 2-го порядка равны нулю то 
.
Если минор 2-го порядка отличен от нуля то исследуем миноры 3-го порядка. Таким образом находят минор 
-го порядка и проверяют, не равны ли нулю миноры 
-го порядка.
Если все миноры 
-го порядка равны нулю, то ранг матрицы 
равен числу 
. Такие миноры 
-го порядка, как правило, находят путем "окантовки" минора 
-го порядка.
Второй метод определения ранга матрицы заключается в применении элементарных преобразований матрицы при возведении ее к диагональному виду. Ранг такой матрицы равно числу отличных от нуля диагональных элементов.
Рассмотрим примеры применения каждого метода.
--------------------------------------------------
Пример 1.
Задание. Найти ранг матрицы 
методом окантовки.
Решение. Матрица 
содержит ненулевые элементы миноры 1-го порядка, следовательно ее ранг может быть равен единице. Согласно правила ранг матрицы не превышает трем 
. Минор 2-го порядка
равен нулю, но следующий минор
отличен от нуля. Окантовывая минор второго порядка проверим третий: для этого разложим его по третьей колонке
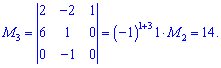
Рассмотрим минор четвертого порядка, окантовывает настоящее
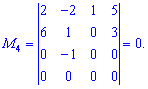
Он равен нулю, поскольку последняя строка нулевой. Остается вычислить еще один минор
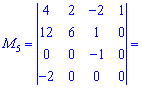
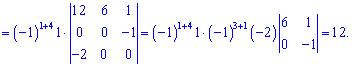
Искомый ранг матрицы равен четырем (
). На примере можно видеть, что выбор окантовки не всегда можно удачно выбрать и нужно числить большое количество миноров.
--------------------------------------------------
Пример 2.
Задание. Найти ранг матрицы 
.
Решение.
1.Переставим четвертый столбец на первое место, а все остальные сместим вправо.
2. Превратим в ноль все элементы в первой строке после 
. Для этого к 
столбцам добавим первый умноженный на 
соответственно.
3. Третий столбец поделим на 
. К четвертого и пятого столбцов добавим третий, умноженный на 
.
4. До пятого столбца добавим четвертый, умноженный на 
.
5. Переставим третий и четвертый столбцы на второе и третье места, а второй столбец на место четвертого.
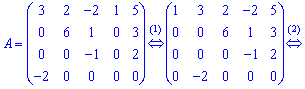
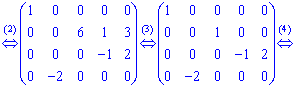
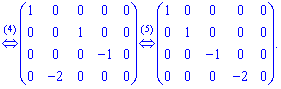
В исходной матрицы вычеркнут последний столбец с нулевыми элементами
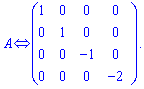
Ранг эквивалентной матрицы равен четырем, а следовательно и 
. Можно заметить, что матрицы в первом и втором примерах эквивалентные между собой (имеют одинаковые ранги).
---------------------------------------------------------------
