Определители четвертого и старших порядков возможно вычислять по упрощенным схемам, которые заключаются в разложении по элементам строк или столбцов или сведении к треугольному виду. Оба метода для наглядности будут рассмотрены на матрицах 4-го порядка.
Метод разложения по элементам строк или столбцов
Первый пример мы рассмотрим с подробными объяснениями всех промежуточных действий.
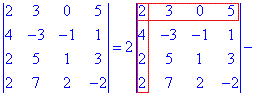
Пример 1. Вычислить определитель методом разложения.

Решение. Для упрощения вычислений разложим определитель четвертого порядка по элементам первой строки (содержит нулевой элемент). Они образуются умножением элементов на соответствующие им дополнения (образуются вычеркивания строк и столбцов на пересечении элемента, для которого исчисляются - выделено красным)
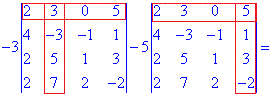
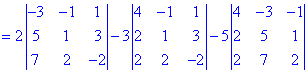
В результате вычисления сведутся к отысканию трех определителей третьего порядка, которые находим по правилу треугольников
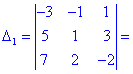
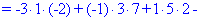
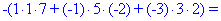
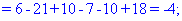
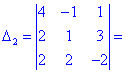
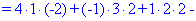
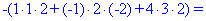
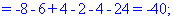
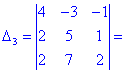
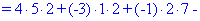
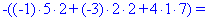
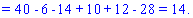
Найденные значения подставляем в выходной детерминант
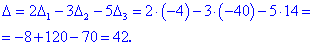
Результат легко проверить с помощью матричного калькулятора YukhymCALC . Для этого в калькуляторе выбираем пункт Матрицы-Определитель матрицы, размер матрицы устанавливаем 4*4.
Далее вводим же матрицу и осуществляем вычисления. Результатом расчетов будет следующий вывод данных

Результаты совпадают, следовательно вычисления проведены верно.
Пример 2. Вычислить определитель матрицы четвертого порядка.

Решение.
Как и в предыдущем задании осуществим вычисления методом разложения. Для этого выберем элементы первого столбца. Упрощенно определитель можно подать через сумму четырех детерминант третьего порядка в виде
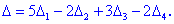
Далее переходим к отысканию определителей по правилу треугольников
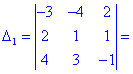
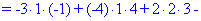
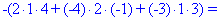
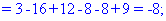
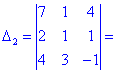
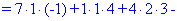
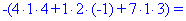
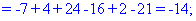
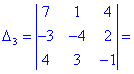
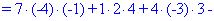
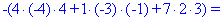
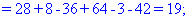
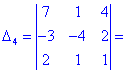
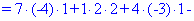
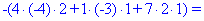
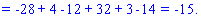
Вычисления не слишком сложные, главное не напутать со знаками и треугольниками. Найденные величины подставляем в главный определитель и суммируем
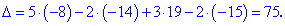
Результат проверяем матричным калькулятором YukhymCALC . Правильность расчетов подтверждается следующим рисунком

Метод возведения определителя к треугольному виду
Данный метод позволяет ряд определителей вычислить достаточно быстрый способ. Суть его заключается в объединении определителя к треугольному виду, при этом следует учитывать все множители на которые увеличиваем или уменьшаем строки и учете при конечных расчетах. Из данного определения Вы ничего для себя не поймете, поэтому лучше все показать на конкретных примерах.
Пример 3. Найти определитель матрицы сведением к треугольному виду
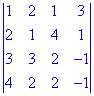
Решение.
Сначала осуществляем математические манипуляции, чтобы получить все нулевые элементы кроме первого в первом столбце. Для этого от второй строки вычитаем первый, умноженный на два. В результате получим
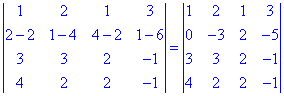
Далее есть два варианта: от третьей строки вычесть первый умноженный на три, или от третьего вычесть сумму первых двух строк. Последний вариант позволит получить сразу два нуля в строке, его и выбираем
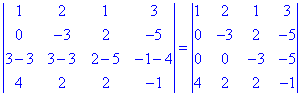
Дальше целесообразнее от четвертой отнять удвоенную вторую строчку. В результате элементарных преобразований определитель примет вид
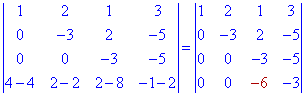
Осталось превратить в ноль один элемент в третьем столбце. Для этого от четвертой строки вычитаем удвоенную третью в предварительно записанном определителе
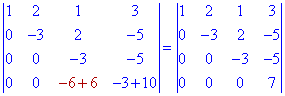
По свойству, определитель треугольной матрицы равен произведению диагональных элементов.
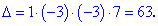
По желанию можно проверить результат матричным калькулятором.

В этом примере никаких умножений строк, в которых зануливали элементы мы не выполняли, поэтому полностью раскрыть метод на этом примере не получилось.
Рассмотрим более сложный.
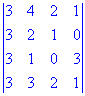
Пример 4.
Найти определитель матрицы 4-го порядка
Решение.
Элементарными преобразованиями сводим определитель к треугольного вида. Для этого от каждой строки вычитаем первый. В результате преобразований получим следующий детерминант
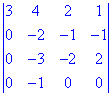
Для удобства вычислений, меняем третью строчку со вторым местами..

По свойству определителей любая замена строк местами ведет к изменению знака определителя. Учитываем это в некотором множителе k=-1.
От третьей строки вычитаем второй, умноженный на минус три. После упрощений получим

Превращаем в ноль последний элемент во втором столбце, для этого вычитаем вторую строчку умноженный на 2.
Результат будет следующим

От удвоенного четвертой строки вычитаем третий. По свойству, умножения строки на постоянную а ведет к изменению определителя в а раз. Данное изменение фиксируем в множителе k=-1*2=-2.

Окончательное значение определителя будет равно произведению диагональных элементов разделенных (или нормированных) на множитель k, который отвечает за изменение детерминанта при элементарных преобразованиях. Выполняем вычисления
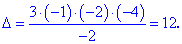
Проверка матричным калькулятором подтверждает правильность производимых вычислений.

Метод разложения определителя по элементам строк или столбцов достаточно быстрым при исчислении определителей больших размеров. Метод сведения к треугольного вида эффективен, если элементарные преобразования легко проследить и не приводят к большим произведений. В других случаях нужно пользоваться комбинацией этих методов, в последнее образовывать как можно больше нулевых элементов, а методом разложения по строкам или столбцам уменьшать количество выполненных операций. Это позволит без проблем вычислять определители третьего, четвертого и даже пятого порядка.


