При нахождении определителей второго, третьего порядка можно пользоваться стандартными формулами (2 - разница произведения диагональных элементов, 3 - правило треугольника). Однако для вычисления определителя четвертого, пятого порядка и старших гораздо быстрее разложить их по элементам строки или столбца, содержащего больше всего нулей и свести к расчету нескольких определителей на единицу меньшего порядка.
Схемы знаков при минорах для детерминантов 3-го - 5-го порядка приведены ниже.
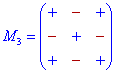
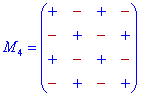
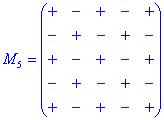
Их не трудно запомнить, если знать следующие правила:
Дополнение к элементам главной диагонали идут со знаком «+», а на параллельных диагоналям чередуются «-», «+», «-», ...
Дополнение к элементам нечетных столбцов и строк начинаются с знака «+», а дальше чередуются «-», «+», для парных начинаются со знака «-», а дальше поочередно меняются «+», «-»,...
Вторым правилом пользуется большинство студентов, поскольку оно привязано к столбца или строки по которому осуществляется расписание определителя.
Перейдем к рассмотрению примеров разложения определителя и изучению особенностей этого метода.
Пример 1.
Разложить определитель третьего порядка по элементам первой строки и второго столбца
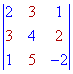
Решение.
Проводим разложение определителя по элементам первой строки
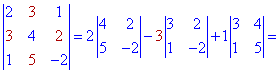
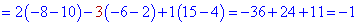
Подобным образом выполняем вычисления разложения по элементам второго столбца
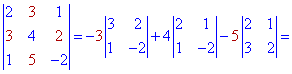
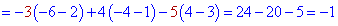
Оба значения одинаковы, а значит расчеты проведены правильно. Если у Вас получится что определители полученные расписанием по строке и столбцу не совпадают - значит где-то допущена ошибка при вычислениях и нужно перечислить или найти ее.
Пример 2.
Найти определитель четвертого порядка методом разложения
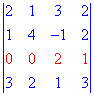
Решение.
Проводим разложение по элементам третьей строки (выделена красным) так как в ней больше всего нулевых элементов.
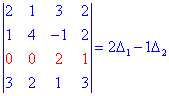
Определители, входящие в расписание находим по правилу треугольников
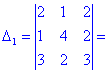
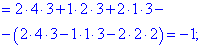
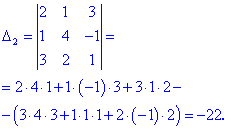
Найденные значения подставляем и посчитываем
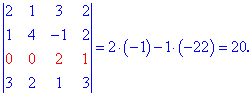
На этом примере метод разложения показал свою эффективность и простоту. Стандартные правила оказались бы слишком громоздкими в вычислениях.
Пример 3.
Найти определитель пятого порядка методом разложения

Решение.
Как и в предыдущем задании ищем строку или столбец содержащие максимальное количество нулевых элементов. Проводим расписание определителя
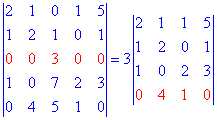
Полученный определитель разложим по четвертой строке
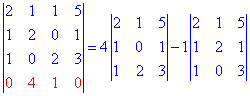
и вычисляем значение
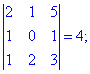
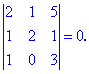
Подставляем в выходной определитель и находим его
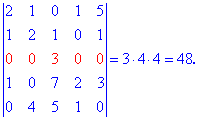
Метод разложения определителя по элементам строк или столбцов является самым быстрым при исчислении определителей больших размеров. Вместо громоздких и сложных вычислений он сводит отыскания определителя к большому количеству простых операций, которые под силу каждому.


