Интерполяционный многочлен Лагранжа применяют при приближении табличных записей данных в виде функции, которая является очень хорошим приближением, если та мало осциллирует и может давать большую погрешность, если для функций со быстросменной производной выбрана малое количество узлов интерполяции
В общем - задано таблицу данных вида
Нужно построить полином, который бы в узлах Х[i] принимал значение Y[i].
Эту проблему решил Лагранж, а искомый полином имеет вид
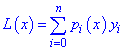
где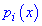 
полиномы на единицу меньшего порядка чем количество данных, вычисляют по формуле
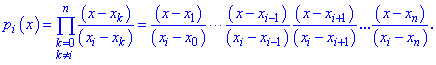
Функции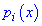 
называют лагранжевими коэффициентами, они обладают свойством
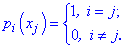
Многочлен вида
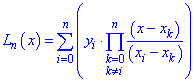
называют интерполяционным многочленом Лагранжа.
Задача 1. Для функции у=cos(Pi*x) построить интерполяционный полином Лагранжа . За узлы интерполяции взять точки x[0]=0; x[1]=1/4; x[2]=1/3; x[3]=1/2. Изобразить функцию и узлы на графике, а также построить оригинал.
Решение:
Вычисляем значения функции в узлах
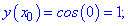
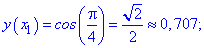
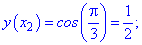
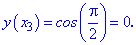
и приводим в виде таблицы
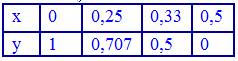
По приведенной выше формуле строим интерполяционный многочлен Лагранжа
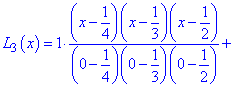
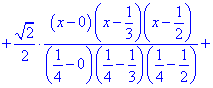
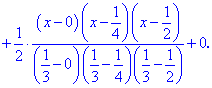
Упрощение вручную мы делать не будем.
Используем для этого математический пакет Maple, в нем задачи по высшей математике , физике, механике , химии решают очень быстро.
Задаем значение функции
> restart;
> with(plots):
>x[0]:=0; x[1]:=1/4;x[2]:=1/3;x[3]:=1/2;
В цикле находим значение функции в точках интерполяции
> for i from 0 to 3 do y[i]:=cos(Pi*x[i]) end do;
Далее строим интерполяционный многочлен
> F:=y[0]*(t-x[1])*(t-x[2])*(t-x[3])/((x[0]-x[1])*(x[0]-x[2])*(x[0]-x[3]))+y[1]*(t-x[0])*(t-x[2])*(t-x[3])/((x[1]-x[0])*(x[1]-x[2])*(x[1]-x[3]))+y[2]*(t-x[0])*(t-x[1])*(t-x[3])/((x[2]-x[0])*(x[2]-x[1])*(x[2]-x[3]));
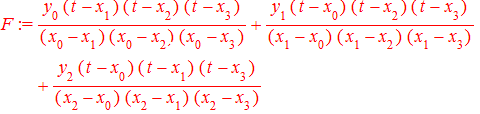
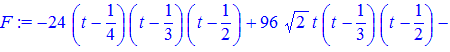
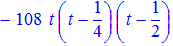
Здесь использована переменная t ,поскольку переменная x имеет тип массива и не может быть использована . Для удобства раскладываем (series) полином Лагранжа по степеням переменой
> G:=series(F,t,4);
Поскольку при переменных в коэффициентах содержатся корни , то округляем (evalf) их до целых значений . В результате получаем функцию третьей степени.
> G1:=evalf(G);
Далее реализуем построение графиков этой функции , оригинала , и значение функции в точках интерполяции .
> Q1:=plot(G1,t=0..1/2,color=black,thickness=2):
> Q2:=plot(cos(Pi*x),x=0..1/2,color=blue,thickness=2):
Записываем функцию отображения суперпозиции графиков
> display(Q1,Q2);
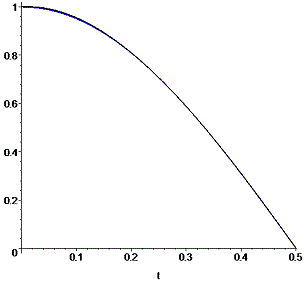
Из графика убеждаемся, что разницы между функцией и оригиналом практически нет.
Рассмотрим другую задачу.
Задача 2.
Данная таблица экспериментальных данных.
Построить интерполяционный полином Лагранжа, а также графики полинома и таблично заданной функции
Решение:
Построим интерполяционный полином Лагранжа по приведенной выше формуле . Для табличных данных он будет иметь достаточно громоздкий вид, поэтому возьмем только его формулу, а остальной анализ выполним в Maple.
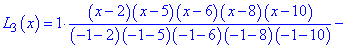
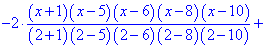
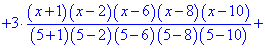
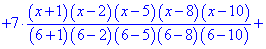
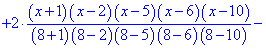
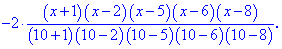
Далее подобные выкладки выполним в Maple. Задаем узлы и значения функции в узлах
> restart; with(plots):
> x[0]:=-1; x[1]:=2;x[2]:=5;x[3]:=6;x[4]:=8;x[5]:=10;
> y[0]:=1;y[1]:=-2;y[2]:=3;y[3]:=7;y[4]:=2;y[5]:=-2;
Далее строим интерполяционный полином Лагранжа . Если правой кнопкой мыши выбрать опцию Standard Math то увидим следующую запись полинома
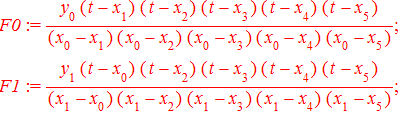
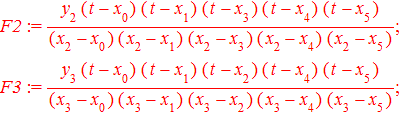
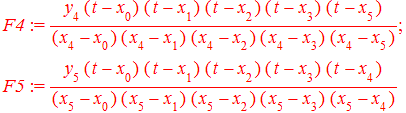
После суммирования слагаемых и разложения в ряд получим полином с дробными коэффициентами
> G:=series(F0+F1+F2+F3+F4+F5,t,6);
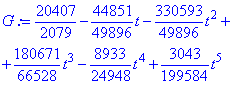
которые после округления упрощаем к виду
> G1:=evalf(G);
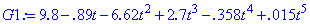
Выполняем построение многочлена Лагранжа
> Q1:=plot(G1,t=-1.5..10.5,color=blue, thickness=2):
> Q2:=plot([[x[0],y[0]],[x[1],y[1]],[x[2],y[2]],[x[3],y[3]],[x[4],y[4]],[x[5],y[5]]],style=point):
> display(Q1,Q2);
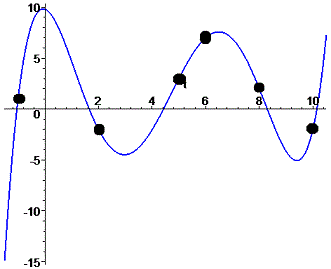
На этом знакомство с интерполяционным полиномом Лагранжа завершается. Используйте многочлен Лагранжа при приближении табличных данных функциями, а также математические программы для упрощения вычислений.
