Формулы сокращенного умножения применяют для упрощения вычислений, а также разложение многочленов на множители, быстрого умножения многочленов. Большинство формул сокращенного умножения можно получить из бинома Ньютона - в этом Вы скоро убедитесь.
Формулы для квадратов применяют в вычислениях чаще. Их начинают изучать в школьной программе начиная с 7 класса и до конца обучения формулы для квадратов и кубов школьники должны знать на зубок.
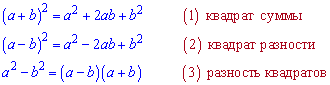
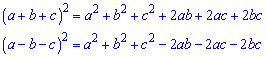
Формулы для кубов не сильно сложные и их нужно знать при сведении многочленов к стандартному виду, для упрощения подъема суммы или разности переменной и числа к кубу.
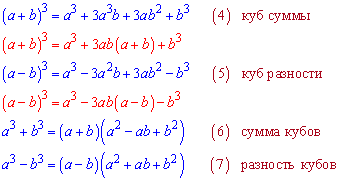
Формулы обозначены красным получают из предыдущих группировкой подобных слагаемых.
Формулы для четвертого и пятого степени в школьном курсе мало кому пригодятся, однако есть задачи при изучении высшей математики где нужно вычислять коэффициенты при степенях.
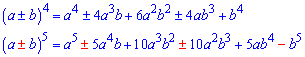
Формулы для степени n расписаны через биномиальные коэффициенты с использованием факториалов следующие
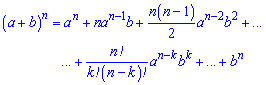
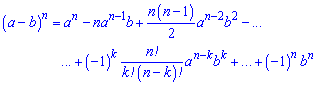
Примеры применения формул сокращенного умножения
Пример 1. Вычислить 51^2.
Решение. Если есть калькулятор то без проблем находите
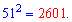
Это я пошутил - с калькулятором мудрые все, без него ... (не будем о грустном).
Не имея калькулятора и зная приведенные выше правила квадрат числа находим по правилу
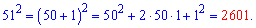
Пример 2. Найти 99^2.
Решение. Применим вторую формулу
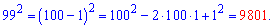
Пример 3. Возвести в квадрат выражение
(x+y-3).
Решение. Сумму первых двух слагаемых мысленно считаем одним слагаемым и по второй формуле сокращенного умножения имеем
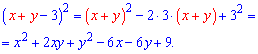
Пример 4. Найти разность квадратов
11^2-9^2.
Решение. Поскольку числа небольшие то можно просто подставить значения квадратов
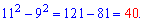
Но цель у нас совсем другая - научиться использовать формулы сокращенного умножения для упрощения вычислений. Для этого примера применим третью формулу
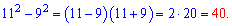
Пример 5. Найти разность квадратов
17^2-3^2.
Решение. На этом примере Вы уже захотите изучить правила чтобы вычисления свести к одной строке
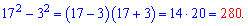
Как видите - ничего удивительного мы не делали.
Пример 6. Упростить выражение
(x-y)^2-(x+y)^2.
Решение. Можно раскладывать квадраты, а позже сгруппировать подобные слагаемые. Однако можно прямо применить разность квадратов
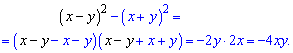
Просто и без длинных решений.
Пример 7. Возвести в куб многочлен
x^3-4.
Решение. Применим 5 формулу сокращенного умножения
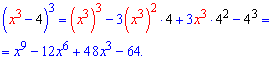
Пример 8. Записать в виде разности квадратов или их сумме
а) x^2-8x+7
б) x^2+4x+29
Решение. а) Перегруппируем слагаемые
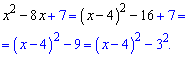
б) Упрощаем на основе предыдущих рассуждений
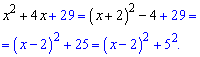
Пример 9. Разложить рациональную дробь
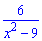
Решение. Применим формулу разности квадратов
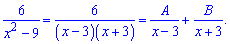
Составим систему уравнений для определения констант
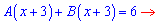
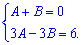
К утроенному первому уравнению добавим второе. Найденное значение подставляем в первое уравнение

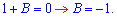
Окончательно разложение примет вид
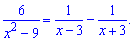
Разложить рациональную дробь часто необходимо перед интегрированием, чтобы снизить степень знаменателя.
Пример 10. Используя бином Ньютона расписать
выражение (x-a)^7.
Решение. Что такое бином Ньютона Вы вероятно уже знаете. Если нет то ниже приведены биномиальные коэффициенты
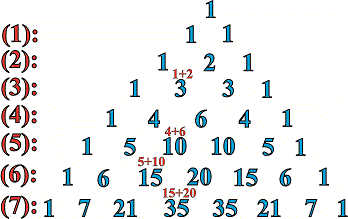
Они образуются следующим образом: по краю идут единицы, коэффициенты между ними в нижней строке образуют суммированием соседних верхних. Если ищем разницу в каком-то степени, то знаки в расписании чередуются от плюса к минусу. Таким образом для седьмого порядка получим такой расклад
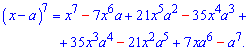
Внимательно также посмотрите как меняются показатели - для первой переменной они уменьшаются на единицу в каждом следующем слагаемом, соответственно для второй - на единицу растут. В сумме показатели всегда должны быть равны степени разложения (=7).
Думаю на основе приведенного выше материала Вы сможете решить задачи на бином Ньютона. Изучайте формулы сокращенного умножения и применяйте везде, где это может упростить вычисления и сэкономит время выполнения задания.


