Уравнение прямой регрессии Y на X. Интервал доверия

Ответы на индивидуальные задания по теории вероятностей на определение числовых характеристик статистического распределения выборки, нахождение уравнения регрессии между двумя признаками, примеры на проверку гипотезы А при существующей гипотезы В помогут успешно сдать сессию студентам. Часть задач разобрана в предыдущей статье, сейчас Вы познакомитесь с методикой составления уравнения прямой регрессии и определения интервала доверия.

Вариант 13. Индивидуальное задание 2.

Задача 1. Связь между признаками Х и Y генеральной совокупности задается таблицей:

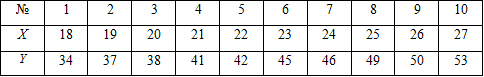
Записать выборочное уравнение прямой регрессии Y на X.
Решение: Вычисляем согласно формул вероятности нужные величины для составления выборочного уравнения регрессии:

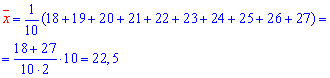
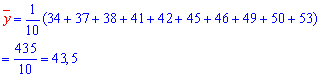
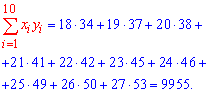
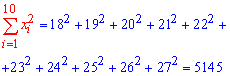
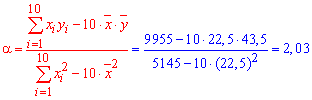
Итак, выборочное уравнение регрессии y=alpha*x+beta
y=2,03*x-2,175.
Вычислим выборочный коэффициент корреляции:

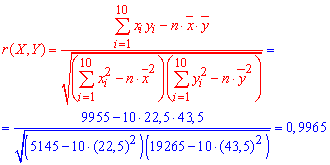
Поскольку выборочный коэффициент корреляции достаточно близок к единице, то предположение о линейности связи между Х и У - правильное. Кроме этого выборочный коэффициент корреляции больше нуля 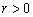, поэтому связь между Х и У положительная и эти случайные величины увеличиваются одновременно.

Задача 2. Найти интервал доверия а для оценки с надежностью неизвестного математического ожидания нормально распределенного признака Х генеральной совокупности:
а) если =0,96, генеральная среднее квадратичное отклонение =5,0, выборочное среднее =21,0, а объем выборки n=36;
б) если =0,99, подправленное среднее квадратичное отклонение s=6,0, выборочное среднее =45,0, а объем выборки n=9.

Решение: а) Из уравнения на функцию Лапласа с помощью таблицы методом интерполяции находим t

Границы интервала доверия ищем по формулам:

Интервал доверия равный с надежностью =0,96.
б) Поскольку объем выборки меньше 30 (n=9<30) и среднее квадратичное отклонение неизвестно, то для нахождения границ интервала доверия используем формулу

где значение ищем с помощью таблиц (распределение Стьюдента):

После вычислений интервал доверия равный с надежностью 0,99.
Задача 3. Найти интервал доверия для оценки с надежностью =0,95неизвестного среднего квадратичного отклонения σ нормально распределенного признака Х генеральной совокупности, если объем выборки n = 11, а подправленное среднее квадратичное отклонение s=9,3.
Решение: Задача сводится к отысканию интервала доверия который покрывает с заданной надежностью =0,95.
По таблице находим
Искомый интервал доверия занимает область или

Как видите вычисления под силу каждому, главное уметь пользоваться формулами и таблицами (распределение Стьюдента). Проверка гипотез на нормальное распределение будет рассмотрена в следующей статье.