Определение уравнения прямой регрессии и интервала доверия

С этого индивидуального задания по теории вероятностей Вы научитесь находить уравнение прямой регрессии двух признаков и находить границы интервала доверия. Эти две величины между собой не связаны, однако на практике в контрольных или тестах встречаются одновременно.

Вариант-8

Задача 1. Связь между признаками Х и Y генеральной совокупности задается таблицей:

Записать выборочное уравнение прямой регрессии Y на X.
Решение: Для построения прямой регрессии Y на X следует сначала найти среднее значение каждой из признаков:

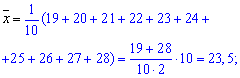
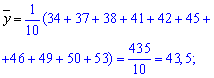
Далее сумму их попарных произведений

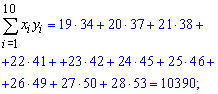
и квадратов значений признака X

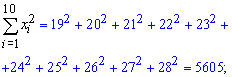
После этого можем посчитать сами коэффициенты, фигурирующие в уравнении прямой регрессии

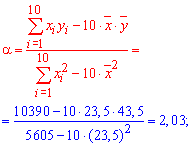
Ну и самая легкая часть - это все подставить в уравнение регрессии y=2,02*x-4,205.С виду формул видим что чрезвычайно сложных операций выполнять здесь не приходится. Однако и здесь многие из Вас умудряются наделать ошибок.
Для подтверждения линейной связи между признаками Y на X следует еще найти выборочный коэффициент корреляции:

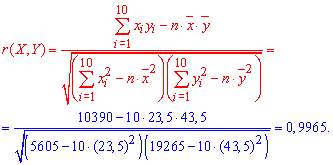
Чем он ближе к единице, тем лучше линейная функция описывает зависимость между признаками. В нашем случае выборочный коэффициент корреляции r(X, Y) практически совпадает с единицей, поэтому делаем вывод что предположение о линейности связи между X и Y правильное. Также коэффициент корреляции больше нуля r>0, что свидетельствует о положительный связь между X и Y, то есть эти случайные величины увеличиваются одновременно.

Задача 2. Найти интервал доверия a для оценки с надежностью γ неизвестного математического ожидания нормально распределенного признака Х генеральной совокупности:

а) если γ=0,96, генеральная среднее квадратичное отклонение σ=5,0, выборочное среднее =28,0, а объем выборки n=25;
б) если γ=0,99, подправленное среднее квадратичное отклонение s=12,0, выборочное среднее =65,0, а объем выборки n=16.

Решение: а) Из уравнения с помощью функции Лапласа методом интерполяции из соседних значений находим t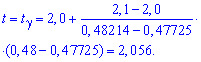

Границы интервала доверия находим с формулами:

Записываем интервал доверия с надежностью 0,96.

б) Поскольку n=16<30 и среднее квадратичное отклонение неизвестно, то для нахождения границ интервала доверия используем формулу

где значение 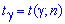ищем с помощью таблиц (распределение Стьюдента):

Итак, интервал доверия равный с надежностью 0,99.

Задача 3. Найти интервал доверия для оценки с надежностью γ=0,99 неизвестного среднего квадратичного отклонения σ нормально распределенного признака Х генеральной совокупности, если объем выборки n = 35, а подправленное среднее квадратичное отклонение s=10,3.
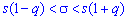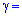Решение: Задача сводится к отысканию интервала доверия который покрывает с заданной надежностью 0,99.
По таблице функции q находим

Искомый интервал доверия лежит в пределах

или

Дочитайте ответы до конца и теория вероятности станет для Вас на шаг понятней и доступней.