Методика проверки гипотез на нормальное распределение

С третьего индивидуального задания Вы изучите методику проверки гипотез на нормальное распределение генеральной совокупности. Разных вариантов всего 5 и все они ниже будут описаны.

Вариант - 8
Задача 1. В таблице приведены эмпирические частоты 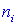и теоретические частоты 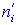рассчитанные исходя из гипотезы H₀ о нормальном распределении генеральной совокупности. Для уровня значимости 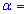0,01 проверить гипотезу H₀ о нормальном распределении генеральной совокупности.

Решение: Вычисляем эмпирическое значение критерия Пирсона (m=5)

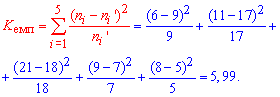
По таблице критических точек распределения хи-квадрат 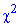для уровня значимости 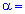0,01 и числа степеней свободы k=m-r-1=5-2-1=2 (r=2 для нормального распределения) находим критическое значение:

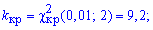
Итак эмпирическое значение меньше критического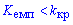 следовательно гипотезу H₀ принимаем.

Задача 2. Для нормально распределенной генеральной совокупности с известным средним отклонениям 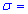0,5 получено выборку объемом n=64 и за ней найдено выборочное среднее 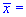77,88. Для уровня значимости 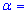0,05 проверить гипотезу 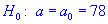при наличии альтернативной гипотезы. .
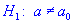Решение: Вычислим эмпирическое значение критерия:

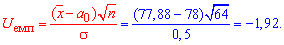
Для альтернативной гипотезы H₁: 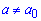находим критическое значение 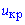по таблице значений функции Лапласа, используя формулы интерполяции

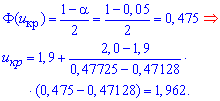
Поскольку эмпирическое значение меньше эмпирическое значение меньше критичного 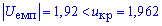, то гипотезу H₀ принимаем.

Задача 3. Для выборки объемом n=16 нормально распределенной генеральной совокупности найдено выборочное среднее 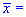89,7 и подправленное среднее квадратичное отклонение s=1,0. Для уровня значимости 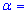0,025 проверить гипотезу H₀: a=a₀=89 при наличии альтернативной гипотезы. H₁: a>a₀.
Решение: Находим эмпирическое значение критерия:

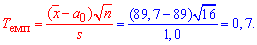
По таблице критических точек распределения Стьюдента для заданного уровня значимости 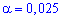(для односторонней критической области) и количества степеней свободы k=16-1=15 находим критическую точку

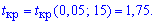
Поскольку эмпирическое значение меньше критического 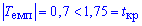, то гипотезу H₀ принимаем.

Задача 4. Для выборки объемом n=21 нормально распределенной генеральной совокупности найдено подправленную дисперсию 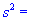13,3. Для уровня значимости 0,1 проверить гипотезу 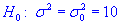при наличии альтернативной гипотезы.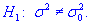
Решение: Находим эмпирическое значение критерия:

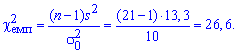
С помощью таблицы критических точек распределения 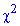определяем «левую» критическую точку

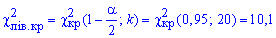
и «правую» критическую точку

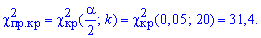
Поскольку условие выполняется 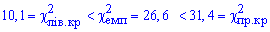, то гипотезу H₁ принимаем.

Задача 5.Для выборки объемом n=15 нормально распределенной генеральной совокупности найдено подправленную дисперсию 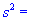6,3. Для уровня значимости 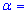0,025 проверить гипотезу 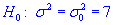при наличии альтернативной гипотезы.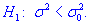
Решение: Вычисляем эмпирическое значение критерия:

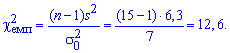
С помощью таблицы критических точек распределения "хи-квадрат"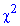 определяем

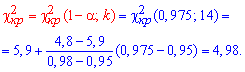
Поскольку условие 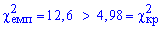имеет место, то гипотезу H₀ принимаем.
Если на контрольной или тестах выполните проверку гипотез подобно приведенной методике, то к теории вероятностей у преподавателей к Вам точно не будет претензий. Для всех остальных случаях обращайтесь за помощью к нам!