Ответы к контрольной работе по теории вероятности помогут студентам первых курсов, изучающих математические дисциплины. Задания охватывают много теоретического материала, а обоснование их решения пригодится каждому студенту.
Задача 1. Куб все грани которого закрашены, распилен на 1000 кубиков одинаковых размеров. Определить вероятность того что кубик вытянутый наугад будет иметь:
- а) одну закрашеную грань;
- б) две закрашеные грани.
Вычисления: Если куб распилить на кубики одинакового размера то все грани будут поделены на 100 квадратов. (Примерно как на рисунке)
Дальше по условию кубик должен иметь одну закрашенную грань - это значит что кубики должны принадлежать внешней поверхности но не лежать на ребрах куба (2 закрашеные поверхности) и не на углах - имеют три закрашеные поверхности.
Следовательно, искомое количество равно произведению 6 граней на количество кубиков в квадрате размером 8*8.
6*8*8=384 – кубики с 1 закрашеной поверхностью.
Вероятность равна количеству благоприятных событий к общему их количеству P=384/1000=0,384.
б) Две закрашеные грани имеют кубики по ребрам без самих вершин куба. На одном ребре будет 8 таких кубиков. Всего в кубе 12 ребер, поэтому две закрашенные грани имеют
8*12=96 кубиков.
А вероятность вытянуть их среди 1000 всех равная
P=96/1000=0,096.
На этом задание решено и переходим к следующему.
Задача 2. На одинаковых карточках написаны буквы А, А, А, Н, Н, С. Какова вероятность того, что случайно разместив карточки в ряд, получим слово АНАНАС?
Вычисления: Нужно рассуждать всегда от того, что известно. Дано 3 буквы А, 2-Н, и 1 - С, всего их 6. Начнем выбирать буквы для слова "ананас". Первой идет буква А, которую мы можем выбрать 3 способами из 6, потому что есть 3 буквы А среди 6 известных. Поэтому вероятность вытянуть первой А равна
P1=3/6=1/2.
Вторая буква Н, но не следует забывать, что после того как вытащили А остается 5 букв для выбора. Поэтому вероятность вытянуть под 2 номером Н равна
P2=2/5.
Следующую А вероятность вытянуть среди 4, что осталось
P3=2/4.
Далее Н можно извлечь из вероятностью
P4=1/3.
Чем ближе к концу тем больше вероятность, и уже А можем извлечь при
P5=1/2.
После этого остается одна карточка С, поэтому вероятность ее вытащить равна 100 процентам или
P6=1.
Вероятность составить слово АНАНАС равна произведению вероятностей
P=3/6*2/5*2/4*1/3*1/2*1=1/60=0,016(6).
На этом и базируются подобные задачи по теории вероятностей.
Задача 3. Из партии изделий товаровед наугад выбирает образцы. Вероятность того что наугад взятое изделие окажется высшего сорта равна 0,8. Найти вероятность того, что среди 3 отобранных изделий будет два изделия высшего сорта?
Вычисления: Данный пример на применение формулы Бернулли.
p=0,8; q=1-0,8=0,2.
Вероятность вычисляем по формуле
Если объяснять не на языке формул, то нужно составить комбинации из трех событий, два из которых благоприятны, а одно нет. Это можно записать суммой произведений
Оба варианта являются равносильными, только первый можем применить во всех задачах, а второй в подобных к рассмотреной.
Задача 4. Из пяти стрелков двое попадают в цель с вероятностью 0,6 и трое с вероятностью 0,4. Что вероятнее: наугад выбранный стрелок попадает в цель или нет?
Вычисления: По формуле полной вероятности определяем вероятность, что стрелок попадет.
P=2/5*0,6+3/5*0,4=0,24+0,24=0,48.
Вероятность меньше P<0,5, следовательно вероятнее что наугад выбранный стрелок не попадет в цель.
Вероятность не попадания составляет
или
P=2/5*(1-0,6)+3/5*(1-0,4)=0,16+0,36=0,52.
Задача 5. C 20 студентов, пришедших на экзамен, 10 подготовлены отлично (знают все вопросы), 7 хорошо (знают по 35 вопросов), а 3 плохо (10 вопросов). В программе 40 вопросов. Наугад вызванный студент ответил на три вопроса билета. Какова вероятность того, что он подготовлен на
- а) отлично;
- б) плохо.
Вычисления: Суть задачи заключается в том что студент ответил на три вопроса билета, то есть на все что были заданы, а вот какова вероятность их вытянуть мы сейчас вычислим.
Найдем вероятность что студент ответил на три вопроса правильно. Это будет отношение количества студентов ко всей группе умноженное на вероятность вытянуть билеты которые они знают среди всех возможных
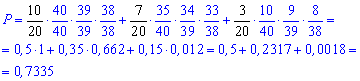
Теперь найдем вероятность что студент принадлежит группе которая подготовлена "на отлично". Это равносильно доле первого слагаемого предварительной вероятности, к самой вероятности
Вероятность, что студент принадлежит группе которая плохо подготовилась достаточно мала и равна 0,00216.
На этом задание выполнено. Хорошо его разберите и запомните как вычислять, поскольку на контрольных и тестах оно распространено.
Задача 6. Монету бросают 5 раз. Найти вероятность того что герб выпадет менее 3 раз?
Вычисления: Вероятность вытянуть герб или решку равносильна и равна 0,5. Менее 3 раз означает, что герб может выпасть либо 0, либо 1, либо 2 раза. "Или" всегда в вероятности в операциях сказывается добавлением.
Вероятности находим по формуле Бернулли
Поскольку p=q=0,5, то вероятность равна
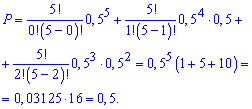
Вероятность равна 0,5.
Задача 7. При штамповке металлических клемм получается в среднем 90% стандартных. Найти вероятность того что среди 900 клемм стандартными будут не менее 790 и не более 820 клемм.
Вычисления: Вычисления необходимо проводить по интегральной теореме Муавра-Лапласа.
Записываем известные величины
n=900; p=0,9; q=1-0,9=0,1; k1=790; k2=820.
Вероятность находим по формуле
где 
интегральная функция Лапласа
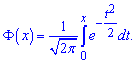
Значение x1, x2 вычисляем по формуле
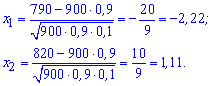
Далее находим вероятность что среди 900 клемм стандартными будут не менее 790 и не более 820
Если объясните подобные задачи так как здесь написано то за контрольную по вероятности получите оценку "отлично".
