Схема Бернулли возникает при повторных независимых испытаниях. Независимыми испытаниями называются такие, которые зависят друг от друга, и от результатов предыдущих испытаний. Они могут проводиться как в однотипных условиях, так и в разных. В первом случае вероятность появления какого-либо события 
во всех испытаниях одна и та же, во втором случае она меняется от опыта к опыту.
Пусть для каждого опыта вероятность появления события равна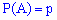 
, вероятность противоположного события определяется зависимостью
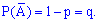
Нужно найти вероятность появления события ровно 
раз в серии из 
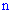испытаний. При этом следует отметить, что событие в серии опытов может чередоваться любым способом, главное чтобы исполнилась ровно раз.
Результаты испытаний для удобства обозначаем буквой в случае появления события и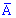 
для противоположного.
Испытания в которых происходит раз и не происходит (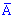
) 
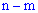раз по определению будут благоприятными. Их количество 
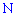равно количеству способов выбора элементов с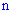 
и определяется по формуле сочетания
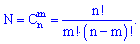
Определим вероятность благоприятной комбинации (в серии из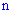 
испытаний появления события ровно раз). Для простоты записи, рассмотрим случай, когда событие произошло в первых опытах и не состоялось в остальных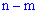 
. Схематично его можно обозначить следующим образом, а вероятность найти по теореме умножения вероятностей
для других благоприятных испытаний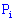 
и вероятности будут такие же, только порядок их в серии из экспериментов будет постоянно меняться
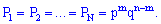
Все благоприятные испытания являются попарно несовместимы, поэтому для нахождения общей вероятности их нужно просуммировать
или
Вывел ее впервые швейцарский математик Якоб Бернулли (1654 г.-1705 г.).
Если просуммировать вероятности всех испытаний в которых событие может произойти от нуля до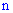 
раз в серии 
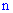испытаний, то получим полную вероятность
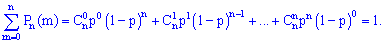
Слагаемые этой суммы совпадают по виду с расписанием бинома Ньютона
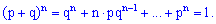
Легко убедится, что
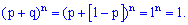
В литературе можно встретить термин "биномиальное распределение вероятностей", это как раз множество всех вероятностей, которые просуммированы выше.
Как последствия, из формулы Бернулли выводятся следующие формулы для популярных для практики задач:
1) вероятность появления события "хотя бы один раз" в серии из 
испытаний
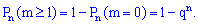
2) вероятность появления события "хотя бы определенное количество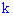 
раз" в серии из 
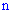испытаний вычисляют по формуле
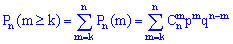
или согласно свойству биномиального разложения вероятностей
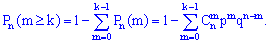
На основе данной зависимости вводят в рассмотрение сквозную функцию, которая дает возможность определить возможное количество появления события в серии из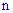 
испытаний
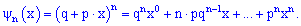
По свойству сквозной функции множители при степени переменной (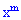
) равны вероятности появления события в серии из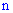 
опытов ровно раз. Это легко проследить по формуле суммирования вероятностей всех возможных испытаний по схеме Бернулли.
Если вероятности появления события в каждом опыте разные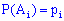 
, а противоположного равны 
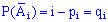то по свойствам сквозной функции вероятность события произойти раз в серии из 
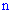опытов равна множителю при 
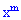в расписании функции по степеням
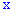
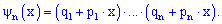
Она достаточно часто встречается при решении задач, в которых вероятности появления события в каждом последующем опыте меняются и позволяет при небольшом количестве появления события быстро найти вероятность (решение задачи).
Вероятное количество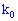 
появлений события в схеме Бернулли лежит в интервале
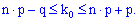
Для применения схемы Бернулли нужно, чтобы выполнялись три условия:
1) опыты должны быть независимы между собой;
2) каждый опыт должен иметь два результата , 
и никаких других вариантов;
3) вероятность появления события должна быть одинаковой для каждого следующего опыта.
Рассмотрим решения типичных для данной схемы задач.
-----------------------------
Пример 1. В тире стрелок проводит 7 выстрелов по мишени с вероятностью попадания каждого 0,8. Какова вероятность того, что будет: а) ровно 4 попадания б) не менее 5 попаданий в) не более двух попаданий.
Решение. а) проводится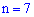 
независимых друг от друга испытаний с вероятностью попадания в мишень в каждом из них 
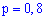. Вероятность того, что будет точно 
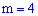попаданий вычисляем по формуле Бернулли:
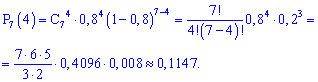
б) событие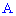 
, которое заключается в том, что при 
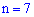выстрелах будет не менее 5 попаданий, можно рассматривать как сумму трех несовместных событий: 
– 5 попаданий из 7, событие 
– 6 попаданий с 7 и 
– все 7 выстрелов метки.
По формуле Бернулли находим вероятности событий
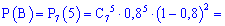
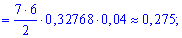
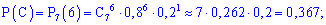
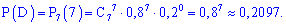
Тогда вероятность события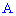 
равна сумме найденных вероятностей
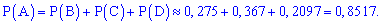
в) Подобным образом, вероятность события – не более двух попаданий при семи выстрелах можно вычислить, как сумму вероятностей трех событий:
– 2 попадания из 7,
– 1 из 7 ,
– ни одного попадания из 7 выстрелов (7 промахов).
На практике студенты часто забывают рассматривать событие - подобное отсутствию попадений 
, поэтому не делайте подобных ошибок и хорошо запомните возможность возникновения такого варианта. Вероятности находим по знакомой уже формуле
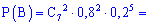
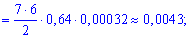
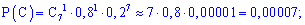
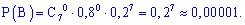
Суммируя вероятности получим
Однако, события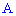 
(не более двух попаданий при семи выстрелах) и (не менее 5 попаданий при семи выстрелах) противоположны друг другу, поэтому
-----------------------------
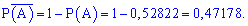
Пример 2. Монета подбрасывают пять раз. Найти вероятность того, что герб выпадет не более трех раз.
Решение. Вероятность выпадения герба или решки считаем независимым событием с вероятностью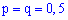 
. По аналогии с предыдущей задачей, искомая вероятность равна сумме трех следующих
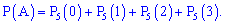
Чтобы не искать столько слагаемых, из приведенных выше формул получим простую
-----------------------------
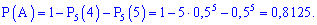
Пример 3. Вероятность появления события в одном опыте равна 0,4. Сколько нужно провести опытов, чтобы вероятное количество появления события была равна 20.
Решение. Согласно условия выписываем данные
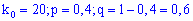
и проводим расчеты согласно неравенству
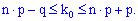
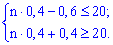
С него получим
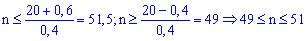
три числа 49,50,51.
-----------------------------
Пример 4. Три биатлониста независимо друг от друга делают по одному выстрелу в мишень. Вероятность попадания в мишень для первого равна 0,9, для второго - 0,85, для третьего - 0,8. Найти вероятность того, что будут закрыты две мишени из трех.
Решение. Вероятности попадания для стрелков разные, поэтому применяем образующую функцию. Для нее входные данные примут значения
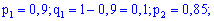
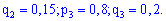
После подстановки и разложения в ряд получим
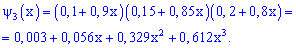
Искомая вероятность входит в расписание множителем при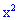 
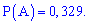
Из этого примера также легко убедиться, что сумма всех множителей при степенях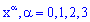 
равна полной вероятности (единицы).
-----------------------------
Схема Бернулли на практике не сложная, важно уловить как в вычислениях реализовать задачи вида "не более раз", "не менее раз", "ровно раз" с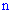 
. Как только Вы это поймете, все остальное сведется к суммирования, умножению и возведения в степень.
