Примеры на интегрирование функций по частям, а также интегралы от квадратных трехчленов взято из материалов контрольной работы, которую задают студентам 1, 2 курсов с математических дисциплин. Для экономии Вашего времени сами условия заданий пропущенные, везде нужно или "Найти неопределенный интеграл" или "Вычислить интеграл". Текста в комментариях к каждому заданию немного, но этого достаточно для усвоения материала и изучение методики и схем интегрирования.
Интегрирование по частям
Пример 8. Здесь необходимо интегрировать частями. Кто не знает как интегрировать по частях то сначала ознакомьтесь с этой статьей. За dv удобно выбрать экспоненту умноженную на dx. Вычисляем v, du и применяем интегрирование по частям
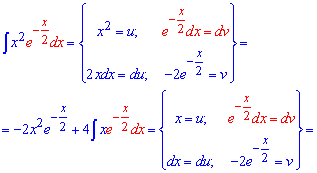
Ко второму интегралу повторно применяем правило интегрирования по частям
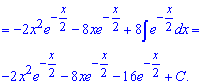
Если бы имели переменную в 3-й степени то интегрировали бы частями трижды и так далее. Другого метода вычислить такого сорта интегралы математики еще не придумали.
Пример 9. В этом интеграле за dv можем обозначать как экспоненту так и синус, поскольку его вторая производная тоже даст синус (со знаком минус). В каждом из случаев придем к рекуррентной формуле с которой и найдем интеграл
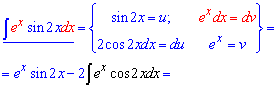
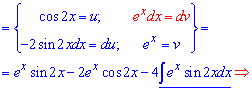
Пришли к рекуррентной формуле, когда справа и слева от знака равенства имеем искомый интеграл
![]()
Группируем слагаемые и делим правую сторону на коэффициент при интеграле
![]()
Пример 10. Несмотря на короткую запись, интеграл от арксинуса двойного «икс» нужно находить интегрированием по частям. Функции u, dv выбираем согласно представленным формулам
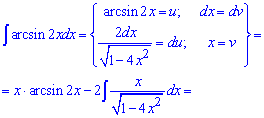
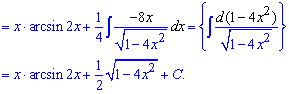
Последние две строки можно расписать переходом к новой переменной, а затем ее подстановки в интеграл, однако и такая запись будет правильным ответом для Вас.
Пример 11. Находим интеграл частями, для этого прямо применяем метод. Здесь в скобках выполняем упрощение в вычислениях дифференциала du
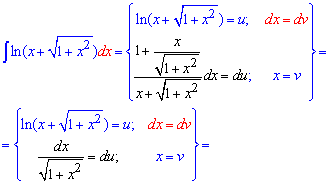
Для применения формулы интегрирования вносим переменную под дифференциал чтобы получить такой же выражение как под корнем
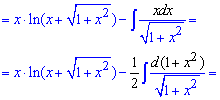
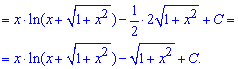
Постепенно Вы запомните что внесение под дифференциал позволяет опускать замены переменных и сразу переходить к готовым формул на интегралы. Теперь Вы знаете как интегрировать частями, другие примеры приведены в конце статьи.
Интегралы, содержащие квадратные трехчлена
Пример 12. Имеем квадратный трехчлен в знаменателе дроби. Для сведения к табличному интегралу следует его свести к разнице или сумме квадратов. В этом задании получим арктангенс
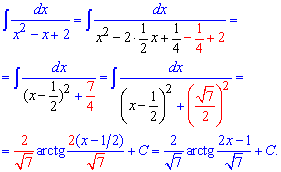
Для легкости чтения формул важные моменты выделены цветом. Поверьте что это помогает быстрее запомнить то, что на первый взгляд выглядит для одних понятным, а другим и после второго и третьего пересмотра тяжелым.
Пример 13. Несмотря на то, что квадратный трехчлен в знаменателе находится под корнем схема возведения к табличному интегралу подобная предыдущему примеру. Разница лишь в том что здесь получим логарифм, а не арктангенс. Важные моменты преобразований записано формулами
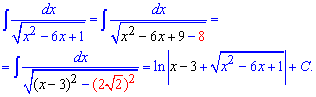
Задания вида 12, 13 на контрольных и тестах встречаются часто, поэтому хорошо их изучите.
Пример 14. В этом интеграле замена переменных несколько специфическая и вряд ли Вы ее запомните, однако без нее интеграл не найти. Поэтому внимательно рассмотрите, как преображается функция под интегралом при такой замене переменных
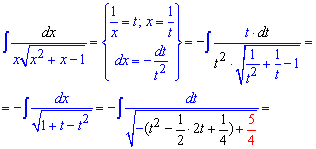
Под корнем в знаменателе выделяем разность квадратов. Поскольку перед скобками, которые содержат переменную стоит отрицательный знак то при интегрировании получим арксинус
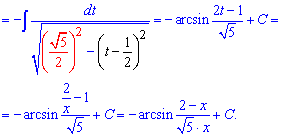
Остальные ответы в следующих материалах. Помните что такого рода примеры задают на контрольных или тестах и внимательно разбирайте ответы к интегралам.
Готовые решения контрольной по интегрированию


