Решение задач на равнобедренный треугольник

Задачи на треугольники требуют знание многих формул, без которых часто трудно получить правильный ответ.
Ниже приведены готовые ответы распространенных на практике примеров, которые подобраны из сборников тестов и школьных учебников. Не рассмотренными в статье остались примеры с множеством вычислений, как, например, применение формулы Герона, или нахождение определенных геометрических размеров. В скором времени и они будут подробно расписаны и объяснены.

Задача 1 Основа равнобедренного треугольника равна 24 см. Найдите радиус окружности, вписанной в треугольник, если проведенная к основанию высота равна 16 см.
Решение: Из курса геометрии известно, что радиус вписанной в треугольник окружности равен отношению его площади к полупериметру. Осталось найти значения двух последних величин.

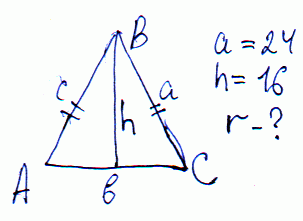
Площадь треугольника по классической формуле равна половине произведения основания на высоту, проведенной к ней. Выполняем вычисления
S=24*16/2=192 (кв. см.)
Для определения периметра нам нужно найти длину боковой стороны.
В равнобедренному треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
По теореме Пифагора находим боковую сторону треугольника
b=sqrt(16^2+(24/2)^2)=20 (см)
Периметр - сумма всех сторон
P=2*20+24=64 (см)
Находим радиус вписанной в треугольник окружности по формуле
r=S/(2*P)=192/(64/2)=192/32=6 (см).
Ответ: 6 (см).

Задача 2 Основание равнобедренного треугольника равно 24 см, боковая сторона 13 см. Вычислите площадь треугольника?
Решение: Площадь равна половине произведения основания на высоту.

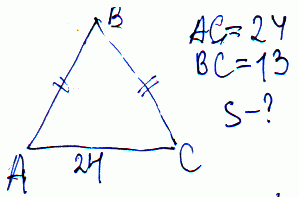
Основание нам известно, высоту находим по теореме Пифагора
h=√(b2-a2/4)= √(169-144)=5 (см).
Далее вычисляем площадь
S=a*h/2=24*5/2=60 (см. кв.)
Ответ: 60 (см. кв.)

Задача 3 Из четырех равных правильных треугольников составили треугольник. Вычислите площадь треугольника DЕF, если периметр треугольника АВС равен 24 см.

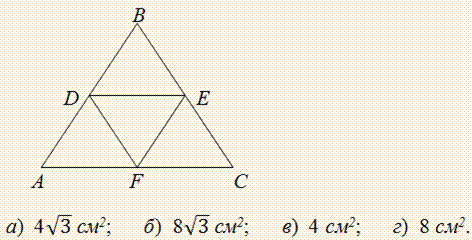
Решение: Под правильным всегда подразумевают равносторонний треугольник.
Разделим заданный периметр на тройку.
a=24/3=8 (см).
Так мы будем иметь сторону большого треугольника. Дальше возможны два пути, или искать сторону малого треугольника и его площадь. Или найти площадь большого треугольника и, по условию, разделить на 4. Рассмотрим второй вариант.
Высота треугольника по Пифагору равна
h=√(8^2-4^2)=4√3 (см).
Найдем площадь треугольника
S=8*4√3/2=16√3 (см. кв.).
Разделив полученное значение на 4 получим искомую площадь треугольника
S1=4√3 (см. кв.)
Такой ответ соответствует первому номеру (А) тестовых вариантов.

Задача 4 Диагональ, боковая сторона и большая основа равнобедренной трапеции равны соответственно 40см, 13 см и 51 см. Найдите радиус окружности, описанной вокруг трапеции.
Решение: Имеем формулу радиуса описанной окружности трапеции по сторонам и диагонали:
R=adc/4√p(p-a)(p-d)(p-c),
где a - боковая сторона, d- диагональ, с - большее основание.
p=(a+d+c)/2=52.
Вычисляем радиус окружности описанной вокруг трапеции
R=26520/(4*√52*39*12*1)=6630/√24336=6630/156= 42,5 см.
Ответ: 42,5 см.

Задача 5 Периметр равнобедренного треугольника 64 см, а боковая сторона на 11 см больше его основания. Найдите высоту треугольника, опущенную на боковую сторону.
а) 13,66 см; б) 13,4 см; в) 13,44 см; г) 15,44 см.
Решение: Составим уравнения по условию.

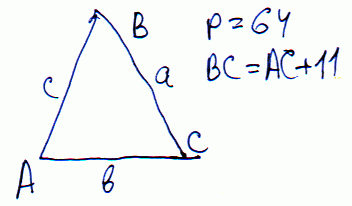
Обозначим основание через Х, тогда боковая сторона – Х+11.
Запишем формулу периметра треугольника
P=2(X+11)+X=3*X+11.
С другой стороны периметр равен 64 см. Получим уравнение
3*Х+22=64 (см);
Х=(64-22)/3=14 (см.)
Боковая сторона равна
X+11=25 см.
Найдем высоту треугольника
h=√ (25^2-(14/2)^2)=24 (см.)
Тогда площадь равнобедренного треугольника равна
S=14*24/2=168 (см. кв.)
Такую же площадь получим, если известна боковая сторона и высота, проведенная к ней
S=h1*25/2=168
Отсюда находим высоту
h1=168*2/25=13,44 (см).
Правильный вариант (в).

Задача 6 Высота равнобедренного треугольника, проведенная к основанию, равна 15 см, а высота, проведенная к боковой стороне – 24 см. Найдите площадь этого треугольника.
а) 270 см²; б) 300 см²; в) 310 см²; г) 285 см².
Решение:Выполняем схематично построение к задаче.

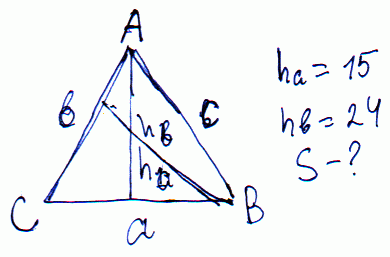
Составим уравнение площади треугольника через известные высоты.
S=a*24/2=b*15/2.
Отсюда имеем отношения для выражения одной стороны через другую
b=24/15*a.
Далее, по теореме Пифагора выразим высоту через боковую сторону и половину основания треугольника
h1=sqrt(a^2-(b/2)^2)=sqrt(a^2-(24*a/15/2)^2)=15 (см.).
Сведя под корнем к общему знаменателю и, выразив неизвестную, получим
a=15*30/18=25 (см.)
Далее находим площадь треугольника
S=24*25/2=300 (см. кв.)
Правильным является вариант (б).

Задача 7 Вычислить площадь равнобедренного треугольника, боковая сторона которого равна 20 см, а высота, проведенная к основанию – 12 см.
а) 192 см²; б) 240 см²; в) 120 см²; г) 96 см².
Решение:

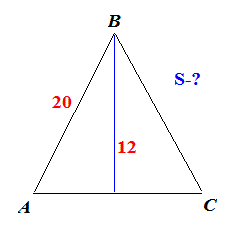
По теореме Пифагора находим основание равнобедренного треугольника
h=sqrt(20^2-12^2)=16 (см).
Находим площадь
S=16*12/2=96 (см. кв.)
Вариант г) является правильным ответом.

Задача 8 Боковая сторона равнобедренного треугольника точкой касания вписанной окружности делится в отношении 12:25, считая от вершины угла при основании треугольника. Найдите радиус вписанной окружности, если площадь треугольника равна 1680 см².

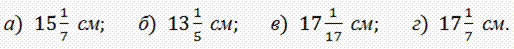
Решение:

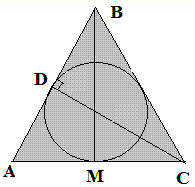
По условию AD/DB=12/25, S=1680.
Обозначим AD=12x, DB=25x.
Из геометрии следует, что AM=12x, а основание треугольника равно 24х.
Из прямоугольного треугольника выразим высоту
h^2=x^2((12+25)^2-12^2).
Далее составим уравнение площади, но для удобства вычислений все умножим на 2 и возведем к квадрату.
(24x)^2*x^2*((12+25)^2-12^2)=(2*1680)^2.
После вычислений получим, что x=2 см.
В соответствии с обозначениями, боковая сторона равна 37*2=74 см , а основание 24*2=48 см.
Радиус вписанной окружности найдем, разделив площадь треугольника на половину периметра.
P=74*2+48=196 см.
P / 2 = 196/2 = 98 см.
r=1680/98=120/7=17 и 1/7.
С тестовых ответов правильный вариант (в).

Задача 9 На медиане ВD равнобедренного треугольника АВС отмечены точки М так, что ВМ:МD=3:1. Найдите площадь треугольника АВС, если площадь треугольника АМD равна 3см².
а) 27 см²; б) 24 см²; в) 30 см²; г) 25 см².
Решение: Многие из Вас подумает, что решить задачу невозможно и нужно применять сложные формулы. Но по большому счету имеем пример на логику. Построим схематически треугольник и изобразим известную область.

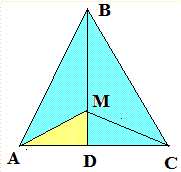
По простой формуле площадь равна половине произведения основания на высоту.
Если рассмотреть треугольники ABD и AMD, то основание в них равно, а высоты относятся как (3+1):1.
Таким образом площадь треугольника ABD в 4 раза больше, чем AMD, а целого равнобедренного треугольника в два раза больше найденного прямоугольного ABD.
Таким образом, площадь S_ABC=2*4*S_AMD=8*3=24 см. кв., что соответствует варианту (б) тестов. Вот такие простые рассуждения позволяют решить непростую на первый взгляд головоломку.

Задача 10 Периметр равнобедренного треугольника равен 100 см, а высота, опущенная к основанию – 30 см. Найдите площадь треугольника.
а) 480 см2; б) 420 см2; в) 560 см2; г) 460 см2.
Решение: Задан пример на составление уравнений.
Обозначим основание треугольника через а, а боковую сторону – b.
Уравнение периметра дает зависимость
P=2*b+a=100.
Запишем формулу квадрата высоты треугольника
b^2-(a/2)^2=30^2.
Из периметра выразим половину основы и подставим во второе уравнение
b^2-(50-b)^2=30^2.
После упрощений получим 100*b=50^2+30^2, отсюда
b=34 см.
а=50 - b=16 см.
Имеем основание и высоту, можем определить площадь треугольника по формуле
S=16*30/2=240 (см. кв.)
На удивление такой ответ отсутствует среди возможных вариантов.

Задача 11 В равнобедренном треугольнике боковая сторона равна 10см, а высота, проведенная к основанию – 6 см. Найти площадь треугольника.
а) 96 см2; б) 60 см2; в) 48 см2; г) 36 см2.
Решение: Выполняем вспомогательный рисунок к примеру.

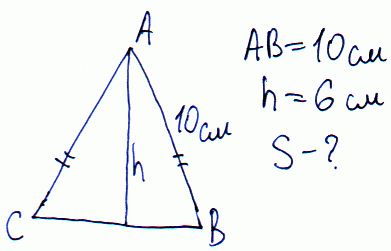
Задания на применение теоремы Пифагора.
Вычисляем половину основания треугольника
a/2=sqrt(10^2-6^2)=8 см. а=2*8=16 см.
После – площадь треугольника
S=16*6/2=48 (см. кв.)
Верным ответом на тестах является вариант (в).

Задача 12 В равнобедренном треугольнике высота, проведенная к боковой стороне, делит ее на отрезки 8 см и 2 см, начиная от вершины угла между боковыми сторонами. Найдите площадь треугольника.
Решение:

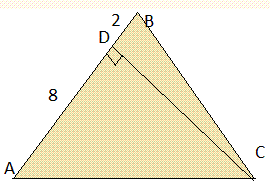
Из рисунка можем подсмотреть сам ход вычислений. Сначала найдем высоту, а дальше площадь.
Гипотенуза треугольника DBC равна
2+8=10 см.
Вычисляем высоту
10^2-2^2=h^2;
h^2=96;
h=4*sqrt(6).
Далее находим площадь
S=1/2*10*4√6=20√6 см².

Задача 13 Периметр равнобедренного треугольника равен 128 см, а боковая сторона относится к основанию, как 5:6. Вычислить диаметр вписанного круга.
Решение: Обозначим основание через 6*a, боковую соответственно – 5*a.

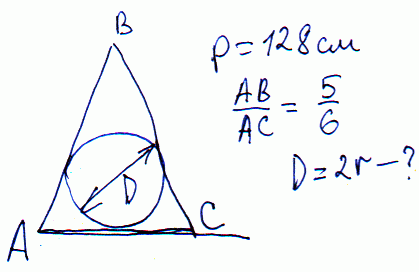
Составляем уравнение периметра
P=2*5*a+6*a=16*a.
Отсюда a=128/16=8 см.
Согласно обозначенным параметрам, основа равна 6*a=48 см,
стороны треугольника 5*8=40 см.
Найдем высоту по известной формуле Пифагора
h=sqrt(40^2-24^2)=32 см.
Вычисляем площадь S=48*32/2-на карте=768 см. кв.
Радиус вписанного в треугольник круга равен отношению площади к половине периметра
R=768/(128/2)=12 см.
Ответ: R=12 см.

Задача 14 Периметр равнобедренного треугольника равен 160 см, а высота, опущенная к основанию равна 40см. Найти все стороны треугольника.
Решение:

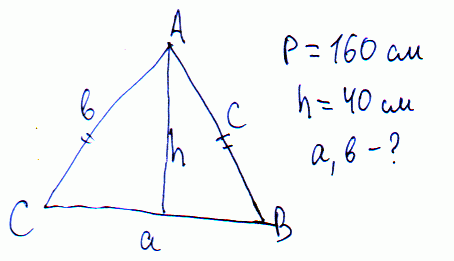
Составляем два уравнения: высоты через теорему Пифагора и периметра.
a+2*b=160;
b^2-(a/2)^2=40^2.
Из первого выражаем a/2 и подставляем во второе
b^2-(80-b)^2=40^2.
Отсюда
160*b=40^2+80^2;
b=50 см.
a=160-2*50=60 см.
Стороны треугольника равны 50, 50, 60 см.

Задача 15 Боковая сторона равнобедренного треугольника равна 55 см, а его основание равно 66см. Вычислить длину отрезков, на которые делит боковую сторону биссектриса угла при основании.
Решение: Обозначим через x, y – отрезки, на которые биссектриса делит боковую сторону.

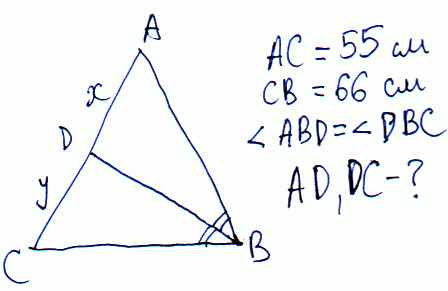
По теореме о пропорциональных отрезках имеем
55/x=66/y, x=55/66*y.
Второе соотношение дает условие, что сумма отрезков равна боковой стороне
x+y=55.
При подстановке первого уравнения во второе получим
(55/66+1)*y=55.
Отсюда y=30 см, x=55-30=25 см.
На этом все вычисления к заданию, рассматрите повнимательней етот ответ.

Задача 16 Боковая сторона и основание равнобедренного треугольника относятся, как 5:6, а периметр его равен 48 см. Найти расстояние от точки пересечения медиан до основания.
Решение: Обозначим стороны треугольника через 5x, 6x соответственно.

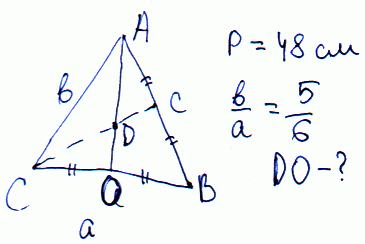
Тогда уравнение периметра запишем в виде
2*5*x+6*x=48;
16*x=48;
х=48/16=3 см.
Отсюда вычисляем основание равнобедренного треугольника
6*x=18 см
и боковые стороны – 5*x=15 см.

Задача 17 Биссектриса, проведенная к боковой стороне равнобедренного треугольника, делит ее на отрезки 25 см и 30 см , начиная от вершины, которая противоположна основе. Вычислить периметр треугольника.
Решение: Обозначим основание и боковую стороны через a, b соответственно.

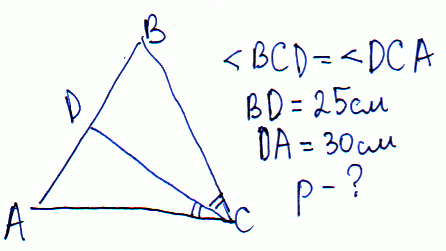
По свойству треугольника составляем зависимость a/30=b/25.
С другой стороны, боковую сторону можем определить
b=25+30=55 см.
Выразим основу с первой зависимости
a=30*b/25=30*55/25=66 см.
находим периметр равнобедренного треугольника
P=66+2*55=176 см.

Задача 18 Боковая сторона равнобедренного треугольника равна 25 см, а высота, опущенная к ней - 24 см. Найти периметр треугольника.
Решение Еще один не простой на первый взгляд пример. Выполняем решения с построение рисунка.

Площадь равна половине произведения основания на высоту. С одной стороны это
S=1/2*25*24=300 см. кв.
С другой стороны обозначим основу через 2x, по теореме Пифагора найдем высоту, а потом и площадь
h=sqrt (25^2x^2);
S=1/2*2*x*sqrt(25^2-x^2).
Приравняв площади, получим уравнение для отыскания основания
x*sqrt (25^2-x^2)=300.
возведем зависимость к квадрату и сгруппируем, в результате получим биквадратное уравнения
x^4-225*x^2+90000=0.
Выполнив замену y=x^2 , сведем его к виду
y^2-225*y+90000=0.
Корни квадратного уравнения равны
y1=400, y2=225.
Отсюда x1=20, x2=15.
Основание треугольника равно 2*x, поэтому в первом случае оно равна 40 см, во втором 30 см . Многим из Вас непонятно, как такое может быть. Дело в том, что при основании 40 высота будет проектироваться не в боковую сторону, а на ее продолжение. Поэтому такой вариант хоть и правильный геометрически, но мы его исключаем. Окончательно периметр равен
P=2*25+30=80 см.

Задача 19 В равнобедренном треугольнике высота, опущенная на основание, равна 32 см. Биссектриса угла при основании пересекает данную высоту в точке, которая удалена от основания на 12 см. Найти основание треугольника.
Решение: Кое-что подправим предварительный рисунок к новому заданию. В «Paint» это делать довольно легко.

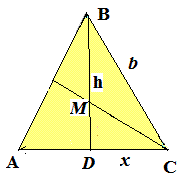
Имеем MD=12, высота h=32 тогда BM=32-12=20 см.
По свойству биссектрисы - она делит высоту на пропорциональные сторонам отрезки, то есть
b/20=x/12.
Второе уравнение получим из теоремы Пифагора
b^2-x^2=h^2=32^2.
Выражаем из первой зависимости одну из неизвестных и подставляем во второе
x=12/20*b;
b^2-(12/20*b)^2= 32^2.
Решение уравнения b=40 см.
Находим вторую неизвестную - x=12/20*40=24 см.
Так, как основание треугольника в два раза больше x, то оно равно 48 см.
Постарайтесь заучить или сгруппировать в памяти подобные схемки вычислений, на контрольной и тестах это помогает в выборе правильного (быстрого) метода расчетов.

Задача 20 В равнобедренному треугольнике угол, образованный высотой, проведенной к основанию, и биссектрисой угла при основании равен 55 градусов. Найти все углы треугольника.
Решение: Выполним вспомогательный рисунок.

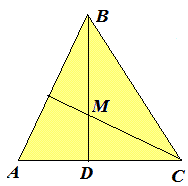
Угол DMC равный 55 градусов. Угол DCM равный 180-90-55=35 градусов.
Поскольку имеем биссектрису, то угол MCB=DCM=35.
Угол при основании равен 2*35=70 градусов.
При вершине равнобедренного треугольника угол равный
180-2*70=40 градусов.
На этом все угловые меры найдено.

Задача 21 В равнобедренному треугольнике основание равно 10 см, а высота – 20 см. Найти высоту опущенную на боковую сторону.
Решение:

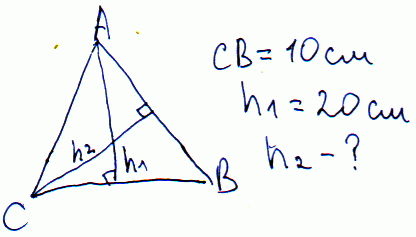
Найдем неизвестную высоту через уравнение площади
S=1/2*20*10=100 см. кв.
Вычислим боковую сторону
b=sqrt(20^2-(10/2)^2)=5√15
и площадь
S=1/2*b*h=100;
Отсюда находим вторую высоту
h₂=2*100/b=8/3*√15 см.

Задача 22 Основание равнобедренного треугольника равно 30 см, а высота опущенная на боковую сторону – 24 см. Вычислить периметр треугольника.
Решение: Обозначим отрезки на которые делит боковую сторону высота через a,x, начиная с основы.

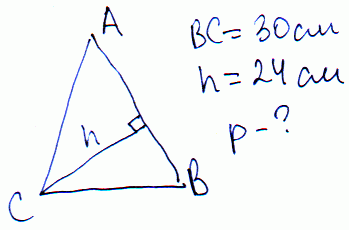
По теореме Пифагора составляем 2 уравнения:
a^2=30^2-24^2;
(a+x)^2-x^2=24^2.
При вычислении системы уравнений получим значение
x=7, a=18.
Отсюда боковая сторона равнобедренного треугольника равна 18+7=25 см, а его периметр
P=30+2*25=80 см.

Задача 23 На медиане равнобедренного треугольника, проведенной к основанию, взята точка, одинаково удаленная от концов боковой стороны. Вычислить периметр треугольника если расстояние от этой точки до основания равно 14 см, а к концу основания – 50 см.
Решение: Без дополнительного построения здесь не разобраться.

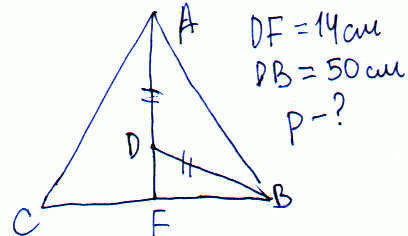
Из рисунка видим, что половину основы можем найти из прямоугольного треугольника
a^2=50^2-14^2
отсюда a=48 см, а основание равно 2*48=96 см.
Также по условию, часть высоты после точки равна 50 см, а вся высота 50+14=64 см.
Из прямоугольного треугольника выражаем боковую сторону
c^2=64^2-48
отсюда c=80 см.
Находим периметр
P=80*2+96=256 см.
Везде где Вам непонятно условие, или что от Вас требуют - используйте вспомогательные рисунки. В большинстве задач это позволяет увидеть ход дальнейших вычислений.

Задача 24 Медиана равнобедренного треугольника, проведенная к основанию, делит высоту, опущенную на боковую сторону на отрезки 75 и 21см, начиная от конца основания. Найдите стороны треугольника.
Решение: Сначала выполняем вспомогательный рисунок

По свойству равнобедренного треугольника медиана проведенная к основанию одновременно является и высотой и биссектрисой. Поэтому с одной стороны можем составить зависимость
x/21=b/75.
С другой стороны, треугольник CDB прямоугольный, поэтому по теореме Пифагора имеем
x^2+(21+75)^2=b^2.
Выразим из первого уравнения x и подставим во второе
x=21/75*b;
96^2=b^2*(21/75* b)^2.
В результате вычислений получим b=100.
Тогда одна из частиц, которую отсекает высота от боковой стороны равна
X=21*100/75=28 см.
Остальная AD равна
AD=100-28=72 см.
Основу равнобедренного треугольника находим как гипотенузу
ADC: 72^2+96^2=a^2.
Отсюда a=120 см.
Стороны равны 120 см и две по 72 см.