Равнобедренный треугольник – это треугольник у которого две стороны или два внутренние углы равны между собой. Другое свойство заключается в том, что высота проведенная к основанию равнобедренного треугольника одновременно является и биссектрисой угла при вершине, и медиане треугольника. Довольно простые свойства, которые выделяют равнобедренные треугольники среди других (прямоугольных, равносторонних).
Для усвоения и повторения материала за 5-6 класс темы "треугольники" напомним их классификацию.
В зависимости от значения углов треугольники делятся на :
- остроугольные;
- прямоугольные;
- тупоугольные.
 В зависимости от длины сторон треугольники делятся на
В зависимости от длины сторон треугольники делятся на
- равносторонние;
- равнобедренные;
- разносторонние.
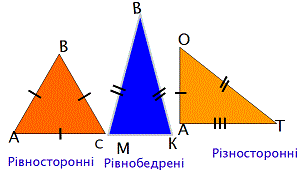
Основные признаки равнобедренного треугольника
1. Если имеем треугольник в котором два угла равны, то он равнобедренный.
2. Треугольник равнобедренный, если:
- одна из его высот является медианой;
- одна из его медиан является биссектрисой;
- одна из его высот является биссектрисой.
3. Треугольник равнобедренный, если:
- две его высоты равны;
- две его медианы равны;
- две его биссектрисы равны.
Начинают изучать треугольники в 5-7 классе в курсе геометрии школьной программы с простых заданий на усвоение определения равнобедренного треугольника, а также на стороны и углы треугольника. Для примера, "Определить углы при основании, если угол при вершине равен 110 градусов". 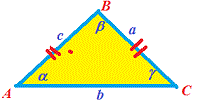
Вычисления таких задач проще простого. Сумма углов треугольника равна 180 градусов, углы при основании (beta) равны. Отсюда на все случаи углов при вершине alpha следует применять формулу
beta=(180-alpha)/2.
Если угол при вершине 110 градусов, то у основания равнобедренного треугольника углы равны
beta=(180-110)/2=35 (градусов).
Пусть задан угол при основании равнобедренного треугольника и он равен 50 градусов, тогда угол при вершине равен
alpha=180-2*50=80 (градусов).
Меняете в формуле значения угла (50) на свой и находите угол в вершине треугольника для любого равнобедренного треугольника.
По мере изучения свойств треугольника, формулы для вписанных и описанных окружностей, возрастает и сложность вычислений и разнообразие задач, которые можно решить. Таким образом в 8-9 классе задачи на треугольники требуют знаний немало важных формул без которых вычисления невозможно выполнить.
Распространенные и самые простые формулы – это периметр и площадь равнобедренного треугольника. Тут никакие свойства треугольника не упрощают указанных величин и их находим по общим формулам треугольника
p=a+b+c;
S=1/2*a*h – площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне. Вторая распространенная формула применяется, если известны стороны и угол между ними.
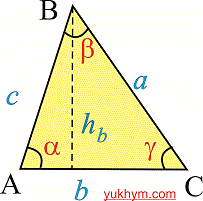
Тогда площадь треугольника равна половине произведения сторон на синус угла между ними. Согласно приведенному рисунку имеем
S=1/2*a*b*sin(hamma);
S=1/2*b*c*sin(alpha);
S=1/2*a*c*sin(beta).
Если задана одна из равных сторон a=b и угол при вершине, то площадь равна
S=1/2*a*a*sin(hamma).
Примеры на равнобедренный треугольник
Часть примеров, что приведены ниже можно назвать устными, поскольку соображения для объяснения вычислений или доказательств можно выполнить в голове без применения ручки и тетради.
Пример 1Является ли равнобедренным любой равносторонний треугольник?
Является ли равносторонним любой равнобедренный треугольник?
Ответ: Любой равносторонний треугольник всегда будет равнобедренным. А вот обратное утверждение не верно. Не все равнобедренные треугольники являются равносторонними, а лишь такие, в которых все стороны или углы равны.
Пример 2. В треугольнике ABC стороны AB=BC равны. Назовите равные углы треугольника.
Ответ: Общей для сторон является вершина В, следовательно, углы при других основаниях равны между собой ∠A=∠C.
Пример 3. Угол между высотой и стороной равнобедренного треугольника равен 30 градусов. Найти угол при основании.
Решение: Поскольку в равнобедренном треугольнике высота является одновременно биссектрисой, то полный угол при вершине равен заданному, умноженному на 2
beta=2*30=60 (градусов).
Вычисляем угол при основании треугольника
alpha=(180-60)/2=60 (градусов).
Поскольку все углы при вершинах треугольника равны, то заданный треугольник является равносторонним.
Пример 4. Какими углами при основании должен обладать треугольник, чтобы он был одновременно и равнобедренным и прямоугольным?
Решение: Прямоугольный треугольник имеет прямой угол (90 градусов) – это знают все. Найдем углы при основании по формуле
alpha=(180-90)/2=45 (градусов).
Таким образом равнобедренный прямоугольный треугольник должен иметь углы 45, 45, 90 градусов.
Пример 5. Высота равнобедренного треугольника равна половине основания. Найти угол при основании треугольника.
Решение: Поскольку высота перпендикулярна основанию и равна ее половине, то угол между основанием и высотой и высотой и стороной равны между собой и составляют 45 градусов. Если Вам это трудно осознать, то приучите себя выполнять построение к условию задания. Многим это помогает быстрее усвоить материал.
Пример 6. Периметр равнобедренного треугольника равен 2,6 м. Найдите стороны треугольника, если его основание больше боковой стороны на 0,5 м.
Решение: В такого типа заданиях нужно составить уравнение. Обозначим сторону треугольника через t. Тогда основание по условию равно
t+0,5 м.
Составляем уравнение для вычисления стороны треугольника
t+t+t+0,5=2,6;
3*t=2,6-0,5=2,1;
t=2,1/3=0,7 (м).
Пример 7. Периметр равнобедренного треугольника равен 20 см.
Найдите:
а) основание треугольника, если его боковая сторона равна 7,5 см;
б) боковую сторону треугольника, если его основание равно 4 см;
в) стороны треугольника, если его боковая сторона относится к основанию как 3:4.
Решение: a) Для вычисления основания из периметра вычтем равные стороны
b=20-2*7,5=6 (см).
б) Найдем боковую сторону равнобедренного треугольника по формуле
a=(20-4)/2=8 (см).
в) Согласно пропорции между стороной и основанием равнобедренного треугольника введем обозначения
сторона равна - 3*Х;
Тогда основание - 4*Х.
Составляем уравнение периметра
3*Х+3*Х+4*Х=20;
10*X=20;
X=20/10=2 (cм).
Вычисляем стороны треугольника
3*2=6 (см)
4*2=8 (см).
Стороны треугольника равны 6, 6, 8 см.
Пример 8. Периметр равнобедренного треугольника ABC равен 18 см, причем основание AC меньше боковой стороны на 3 см. Найдите основание треугольника ABC
Решение: Вводим обозначения: основание – Х, сторона Х+3.
Составляем уравнение
Х+2*(Х+3)=18;
3*Х=18-6=12;
Х=12.3=4 (см).
Ответ: основание треугольника равна 4 см
Задачи на площадь треугольника
Задача 1. Стороны равнобедренного треугольника 5 см, основание – 6 см Найдите площадь треугольника .
Решение: Сначала выполняем построение к задаче. 
Для вычисления площади нам кроме основы нужно найти высоту треугольника. Известно, что высота является медианой равнобедренного треугольника, то есть делит основание на два отрезка по 6/2=3 (см). Далее вычисляем высоту ка катет прямоугольного треугольника
h^2=5^2-3^2=25-9=16;
h=sqrt(16)=4 (см).
Вычисляем площадь треугольника
S=1/2*6*4=12 (сантиметров квадратных).
Ответ: 12.
Задача 2. Стороны равнобедренного треугольника 10 см, а высота опущенная к основанию – 8 см. Найдите площадь треугольника .
Решение: Построим треугольник. Половину стороны основания обозначим через x. По теореме Пифагора составим уравнение
8^2+x^2=10^2;
x^2=100-64=36;
x=6 (см).
Полное основание в два раза больше – 12 см. Находим площадь треугольника
S=12*8/2= 48 (сантиметров квадратных).
Задача 3. Стороны равнобедренного треугольника равны 5, 5, 6 см. Найти радиус окружности описанной вокруг треугольника.
Решение Для вычисления радиуса описанной вокруг треугольника окружности необходимо знать формулу
Поскольку стороны известны то площадь можем найти через формулу Герона, однако это сложный путь. Проще по теореме Пифагора найти высоту треугольника. Поскольку высота является перпендикуляром к основанию и, одновременно медианой, то высота равна катету прямоугольного треугольника с гипотенузой 5 см и катетом
6/2=3 см .
Вычисляем высоту

 (см).
(см).
Находим площадь треугольника
S=1/2*6*4=12 (см. кв.).
Имеем все данные для вычисления радиуса окружности
R=5*5*6/12=12,5 (см).
Ответ: радиус окружности равен 12,5 см.
В интернете немало примеров на равнобедренный треугольник. Часть из них похожи к рассмотренным задачам, другие - более сложные и требуют применения большего количества формул. Свойства равнобедренного треугольника часто встречаются в задачах на ромб, пирамиду, трапеции. Поэтому, изучив базовые формулы и правила на простых фигурах, на сложных применять знания становится намного проще.

