Целочисленных случайная величина Х имеет равномерный закон распределения, если вероятности ее возможных значений одинакова от эксперимента к эксперименту и вычисляются формуле
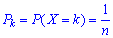
В табличной форме записи равномерный закон распределения имеет вид:
Условие нормировки для равномерного закона распределения имеет вид
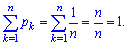
Вероятностная образующая функция на основе первой формулы принимает значение
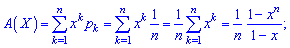
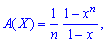
или
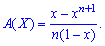
Числовые характеристики равномерного закона находим на основе образующей функции
1. Математическое ожидание находим по формуле
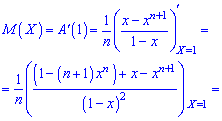
При х = 1 получаем неопределенность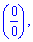 
которую раскрываем по правилу Лопиталя
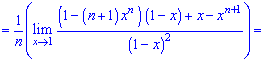
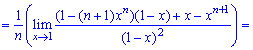
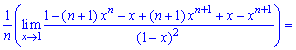
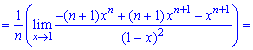
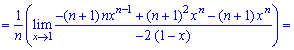
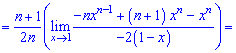
При х = 1 нова имеем неопределенность вида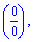 
которую также раскрываем по правилу Лопиталя
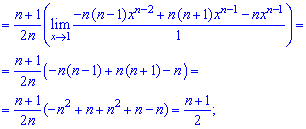
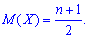
Вычисление заняли богатая времени, однако формула для математического ожидания получилась довольно легкой.
2. Выполнив подобные, но более громоздкие преобразования, дисперсию и среднее математическое отклонение находим по формулам
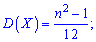
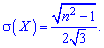
3. Для равномерного распределения вероятностей асимметрия и эксцесс равны нулю
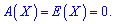
Есть и другое определение, согласно которому функция имеет равномерное распределение, если некотором интервале плотность вероятностей принимает постоянное значение
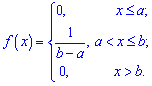
Функция распределения вероятностей для равномерного закона определяется интегрированием
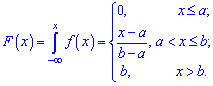
Математическое ожидание в таких случаях определяют зависимости
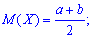
дисперсию по формуле
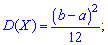
и среднее квадратическое отклонение через корень
Вероятность попадания случайной величины Х в некоторый интервал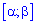 
, содержащийся внутри интервала 
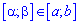определяется по формуле
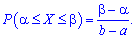
Приведенные формулы часто являются применимыми на практике чем те, которые были даны выше.
Рассмотрим примеры отыскания числовых характеристик.
------------------------------------------
Пример 1. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение М (Х), D (X), S (Х), Найти математическое ожидание, дисперсию и среднее квадратическое отклонение Х имеет равномерный закон распределения и возможные значения ее значение лежит в диапазоне 1..50:
.
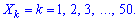Решение. По условию задачи имеем следующие данные n = 50, p = 1/50=0,02.
Согласно формулам вычисляем математическое ожидание
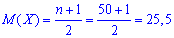
дисперсия
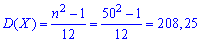
среднее квадратическое отклонение
-------------------------------------------
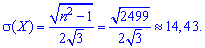
Пример 2. Поезда в метро прибывают на станцию ??каждые 10 минут. Определить вероятность того, что время ожидания состава не будет больше 4 минуты.
Решение. По условию задачи имеем два интервала
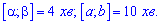
Согласно формуле, искомая вероятность равна доле этих величин
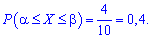
Задачи на отыскание интервала попадания случайной величины, распределена по ривнимирним законом решайте по такой же схеме. Она проста и не требует сложных вычислений.
