Гипергеометрический закон распределения вероятностей столь тяжелый при первом ознакомлении, что лучше всего его объяснять на конкретном примере.
Пусть задано некоторое множество однотипных элементов, число которых равно N; из них K элементов имеют, например, признак А (цвет, стандартность, наполнения), а остальные N-K элементов - признак В. С этого множества наугад берут n еэлементов. Случайная величина X – число элементов с признаком вида А, что случается среди n наугад взятых элементов. Тогда X принимает значения k=0,1,2,...,min(n,K) , а вероятность их появления определяется гипергеометрическим законом распределения
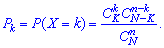
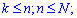
В табличной форме записи этот закон распределения имеет вид
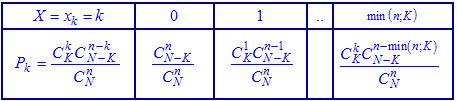
Напомним, что сочетание находим по формуле
а факториал функцию по правилу–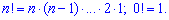 
При n=k і k=0 сочетание равное единице.
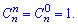
Условие нормировки для гипергеометрического распределения имеет вид
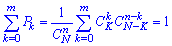
В зависимости от условия задачи наименьшее значение может составлять m = 0, 1, 2, 3, ..., m.
Числовые характеристики этого закона вычисляются по приведенным ниже формулам:
1. Математическое ожидание
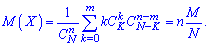
2. Дисперсия и среднее квадратическое отклонение
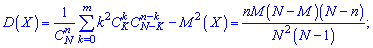
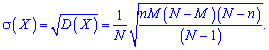
3. Для асимметрии
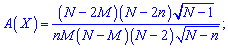
и эксцесса
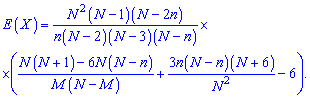
формулы имеют довольно громоздкий вид, поэтому их, как правило, вычисляют в Эксель, или математических программах (Maple, MathCad, Mathematica).
Рассмотрим несколько примеров на применение приведенных выше формул
-----------------------------------------
Пример 1. В ящике содержится 10 однотипных деталей, из них 7 стандартных, а остальные являются бракованными. Наугад из ящика берут m деталей. Построить законы распределения целочисленной случайной величины Х — появление числа стандартных деталей среди m наугад взятых и вычислить математическое ожидание М(Х), дисперсию D (X), и среднее математическое отклонение S(Х), если:
I. m = 3; II) m = 4; III) m = 5; IV) m = 7.
Решение. Используя формулу (253) построим гипергеометрические законы распределения:
I. Имеем следующие начальные условия для случая выбора трех деталей
n = 3; N=10; K= 7; N-K= 3; k = 0, 1, 2, 3.
В табличной форме гипергеометрический закон для этих данных имеет вид
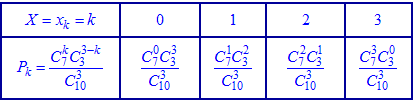
или после вычисления сочетаний
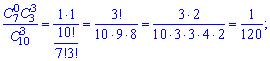
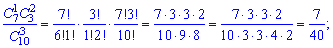
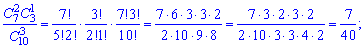
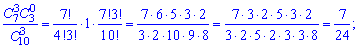
в виде таблицы вероятностей
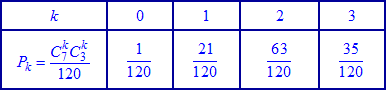
Условие нормирования
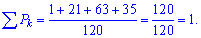
выполняется, следовательно все верно посчитано. Не ленитесь проверять его, оно намного скорее укажет Вам на присутствие ошибки при неправильной правой части. Вычисляем числовые характеристики:
Математическое ожидание
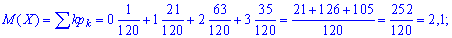
Дисперсию
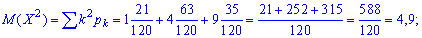
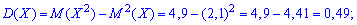
Среднее квадратичное отклонение
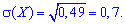
ІІ. Выбирают четыре детали
n = 4; K= 7; N-K= 3; k = 1, 2, 3, 4.
В табличной форме закон распределения запишется формулами
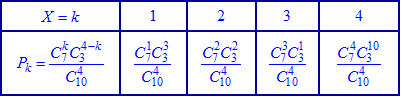
или после вычислений в виде таблицы
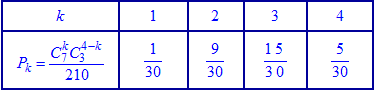
Проверяем условие нормировки для найденных значений
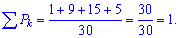
Оно выполняется, следовательно можем вычислять числовые характеристики по приведенным выше формулам:
математическое ожидание примет значение
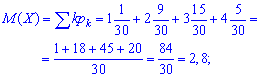
дисперсию и среднее квадратичное отклонение определяем по схеме предыдущей задачи
.
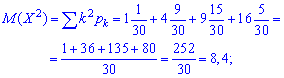
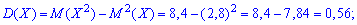
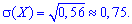ІІІ. Выбирают пять деталей
т = 5; K = 7; N-K = 3; k = 2, 3, 4, 5.
В табличной форме закон подается в виде
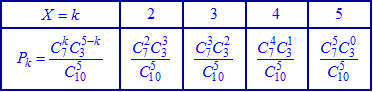
или таблицы значений
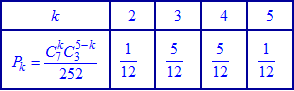
Условие нормирования
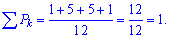
выполняется. Вычисляем математическое ожидание
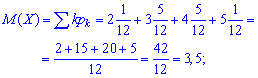
Составляющую дисперсии
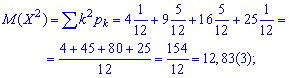
дисперсию и среднее квадратичное отклонение
.
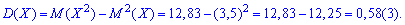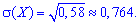
IV.) Выбирают семь деталей
т = 7; K= 7; N-K= 3; k = 4, 5, 6, 7.
В табличной форме данное деление принимает значение
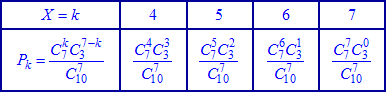
или после вычислений
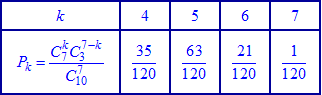
Условие нормирования
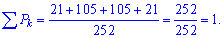
выполняется.
Числовые характеристики определяем на основе формул:
математическое ожидание
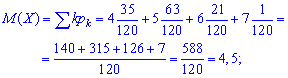
математическое ожидание квадрата величины
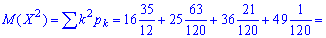
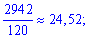
дисперсию
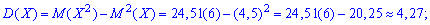
среднее квадратичное отклонение
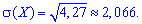
На этом решение задачи завершено. Будьте внимательны при решении примеров на гипергеометрическое распределение, поскольку достаточно часто требуется находить сочетание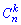 
и при упрощении факториалов можно допустить ошибку.
