Ответы на последние вопросы ВНО по математике актуальные и их чаще всего ищут в интернете. Дело в том что за эти задачи можно получить большое количество недостающих баллов и мало кому из участников удалось правильно решить указанные задачи. Данные варианты взяты из второй сессии тестирования 2013 года.
------------------------------
Задача 29. В прямоугольный треугольник АВС вписана окружность, которая примыкает к катетам АС и ВС в точках К и М соответственно. Найдите радиус окружности описанной вокруг треугольника АВС (в см) если АК= 4,5см, МВ= 6см.
Решение: Для решения задачи нужно знать свойства кругов вписанных и описанных вокруг треугольника, причем сами вычисления достаточно просты. Построим вспомогательный график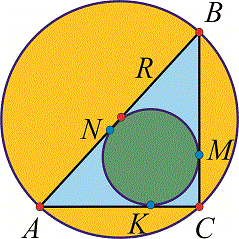
По свойству отрезков на которые делит вписанная окружность катеты в точках соприкосновения имеем:
AN=AK, CK=CM, BN=BM.
На основе выше изложенного вычисляем длину гипотенузы треугольника
AB=AN+BN=AK+MB=4,5+6=10,5 (cм).
Поскольку радиус описанной окружности равен половине гипотенузы то осталось разделить найденное значение н 2
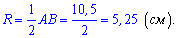
Ответ: 5,25 .
------------------------------
Задача 30. Вычислите площадь фигуры которая ограничена графиком функции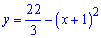 
и прямыми 
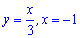та 
.
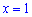Решение: Для отыскания площади фигуры нужно выяснить взаимное расположение кривых. Ниже приведены рисунок с закрашеной областью, площадь которой нужно найти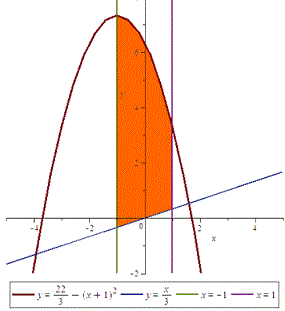 
При тестировании Вы точно не будете иметь подобного рисунка, а вычислять интеграл придется. В этом случае нужно провести следующий анализ. Интегрирование, как правило, проводят по переменной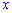 
. По данным прямые 
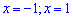будут пределами интегрирования.
Осталось установить какая из кривых
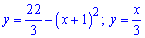
находится выше на рисунке, а какая ниже. Если этого не сделать то площадь может выйти отрицательной. Для проверки находим значение в точке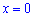 
которая принадлежит области интегрирования
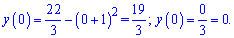
Итак первая кривая находится выше. По правилу нахождения площадей - от верхней кривой вычитаем нижнюю и интегрируем в пределах [-1;1]
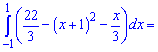
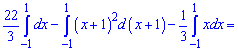
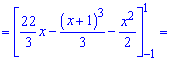
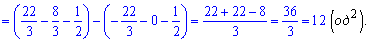
Ответ: 12 .
------------------------------
Задача 31. В фестивале принимают участие 25 групп среди которых есть по одной группе из Украины и Чехии. Порядок выступления групп определяется жеребьевкой согласно котрой каждая из групп имеет одинаковые шансы получить любой номер от 1 до 25. Найдите вероятность того что на этом фестивале группа из Украины будет выступать первой, а порядковый номер выступления группы из Чехии будет четным.
Решение: Пусть событие А – Украина выступает первой, событие В – Чехия выступает под четным номером. Вероятность определяем по классической формуле
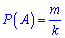
Вероятность что Украина выступит первой равна
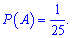
После выполнения события А останется 24 команды, каждая вторая из которых может выступить под четным номером, то есть
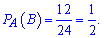
По правилу находим вероятность через произведение
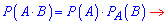
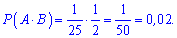
Ответ: 0,02
------------------------------
Задача 32. Основанием пирамиды является ромб, тупой угол которого равен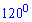 
. Две боковые грани пирамиды содержащие стороны этого угла перпендикулярны к плоскости основания, а две другие боковые грани наклонены к плоскости основания под углом 
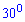. Найдите площадь боковой поверхности пирамиды (в 
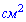), если ее высота равна 4 см
Решение: Приведем вспомогательный рисунок на основе данных задачи.
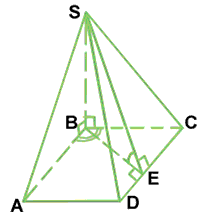
Пусть SABCD – пирамида, ABCD – ромб в ее основе.
Два угла основы известны
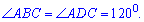
Находим соседние углы
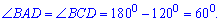
Высота основания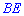 
перпендикулярна к стороне 
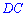. Также с перпендикулярности боковых граней пирамиды следует следующее
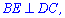
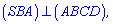
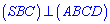
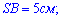
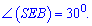
Треугольники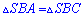 
равны, поскольку в них одна сторона 
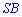общая, 
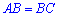и углы при основании прямые
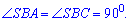
Это означает что стороны равны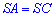 
и треугольники 
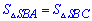. По свойству ромба также получим следующие равенство
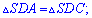
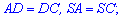
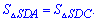
На основе вышеизложенного боковая поверхность пирамиды вычисляется суммированием
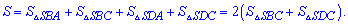
Площади треугольников можно найти по формулам
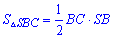и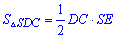 
которые после подстановки дают такой вклад
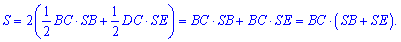
Рассмотрим по очереди два треугольника
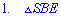
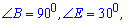
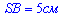– катет напротив угла 
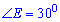равен половине гипотенузы 
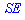- отсюда находим гипотенузу
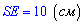
и длину второго катета
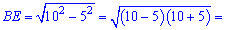
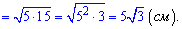
Также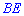 
является высотой равностороннего треугольника 
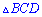, поскольку получим что все углы равны 
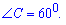А это значит что 
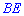можно определить по формуле
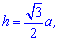где 
– сторона равностороннего треугольника (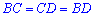
).
Таким образом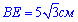 
и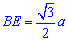 
. Приравниваем значение для отыскания стороны
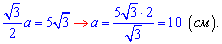
Имеем все необходимые значения для нахождения площади боковой поверхности пирамиды
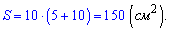
Ответ: 150.
------------------------------
Задача 33. При каком самым большем отрицательном значении параметра 
уравнения
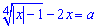
имеет один корень ?
Решение: Уравнение достаточно сложное поэтому пойдем простым путем. Известно что параметр 
отрицательный, соответственно левая сторона уравнения также отрицательная. Однако она содержит корень четвертой степени который всегда положительный для всех значений с ОДЗ .
Перепишем уравнение в виде
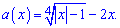
Найдем ОДЗ
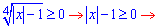
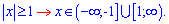
Поскольку параметр 
меньше нуля то значения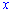 
должны быть положительными.
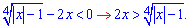
Из этого следует что для положительных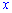 
модуль можно снять
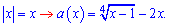
Для нахождения наибольшего значения вычислим первую производную функции и приравняем ее к нулю
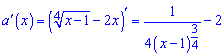
Определим критические точки, для этого решаем уравнение
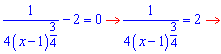
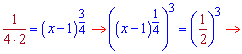
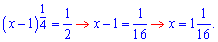
Для проверки что найденная точка является точкой максимума необходимо убедиться, что она меняет знак с «+ » на «-». Поскольку производная дала одну точку, а нам нужна точка максимума, то не думаю, что задачу придумывали так, чтобы она не имела правильного ответа.
Подставим найденные значения в формулу и найдем наиболее отрицательное значение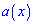 
на промежутке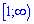 
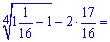
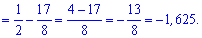
Ответ: -1,625.
------------------------------
Посмотрите ВНО математика. Решение задач № 23-28
