Решения тестов ВНО-2013 по математике помогут в подготовке к тестированию и будут актуальными и в 2014, 2015 годах. Очевидно, что таких задач там не будет, однако можно очертить круг подготовки - какие разделы математики следует проработать чтобы быть успешными на тестах. Поэтому разбирайтесь с ответами к задачам и легкой Вам сдачи ВНО.
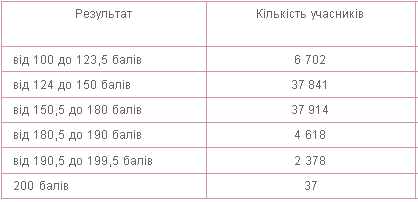
Результаты участников ВНО по математике в 2013 году:
Вторая сессия ВНО по математике ( 2013 )
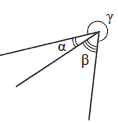
Задача 1. Три луча с общим началом лежат в одной плоскости (см. рисунок). Определите градусную меру угла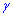 
, если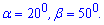 
Варианты ответов :
А)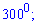 
Б)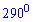 
В)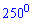 
Г)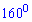 
Д)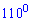 
Решение: Сумма всех углов составляет 360 градусов
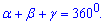
Отсюда вычисляем неизвестный угол
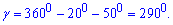
Ответ: Б.
------------------------------
Задача 2. Диаграмма изображенная на рисунке содержит информацию о количестве электроэнергии (в кВт.*ч. ) потребленной определенной семьей в каждом месяце 2012 года. Пользуясь диаграммой установите какие из приведенных утверждений являются правильными.
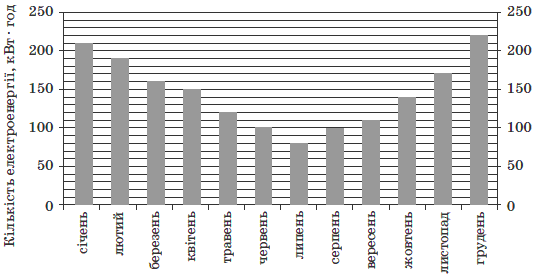
І. В декабре по сравнению с июлем потреблено электроэнергии больше чем в 2 раза.
ІІ. За все летние месяцы потреблено электроэнергии на 150 кВт*ч меньше чем за все весенние месяцы.
ІІІ. Среднемесячное потребление электроэнергии за год является больше 120 кВт*ч
Варианты ответов :
А) только І,
Б) только І і ІІ,
В) только І і ІІІ,
Г) только ІІ і ІІІ,
Д) І, ІІ і ІІІ.
Решение: В декабре потребили 280 кВт*час, в июле – 80 кВт*час. То есть в декабре по сравнению с июлем потребили в
280/80=3,5
электроэнергии больше (чем в 2 раза).
За летние месяцы потреблено
100+80+100=280 кВт*час
Находим суму весенних месяцев
160+150+120=430 кВт*час.
Разница составляет
430-280=150 кВт*час,
То есть за летние месяцы потреблено на 150 кВт*час меньше чем за весенние
Среднемесячное потребление электроэнергии за год находим как среднее арифметическое всех месяцев
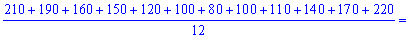
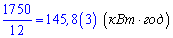
и составляет более 120 кВт*час.
Ответ : Д.
------------------------------
Задача 3. Остаток от деления натурального числа k на 5 равно 2. Найдите остаток от деления на 5 числа k+21.
Варианты ответов:
А) 0,
Б) 1,
В) 2,
Г) 3,
Д) 4.
Решение: Поскольку число k делится на 5 с остатком 2 то его можно записать в виде
k=5l+2,
где l – произвольное натуральнее число.
Тогда k+21 можно записать в виде
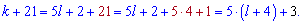
Из этой записи даже без операции деления видим что остатком от деления будет число 3.
Ответ: Г.
------------------------------
Задача 4. В геометрической прогрессии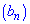 
задано 
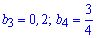. Найдите знаменатель этой прогрессии.
Варианты ответов:
А)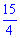 
Б)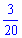 
В)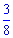 
Г)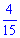 
Д)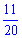 
Решение: По свойству геометрической прогрессии каждый следующий член отличается от предыдущего постоянным множителем, который называется - знаменатель геометрической прогрессии
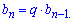
На основе данных вычисляем знаменатель прогрессии.
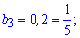
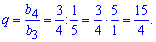
Ответ А.
------------------------------
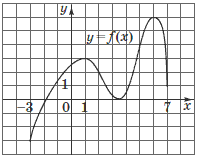
Задача 5. На рисунке изображен график непрерывной функции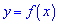 
определенной на отрезке 
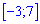. Сколько всего точек экстремума имеет эта функция на отрезке 
?
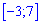Варианты ответов:
А) 1
Б) 2
В) 3
Г) 5
Д) 6
Решение:Точками экстремума являются локальные минимумы и максимумы функции.
Функция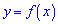 
имеет максимум (минимум) в точке 
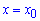если значение функции в этой точке больше (меньше) значения в соседних точках справа и слева от точки 
.
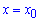Значения функции в точках минимума и максимума называется экстремумами функции
Из рисунка видно что таких точек на отрезке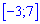 
всего 3 - два максимума в точках 
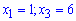и один минимум при значении аргумента 
.
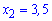Графически на рисунке они изображены красными точками
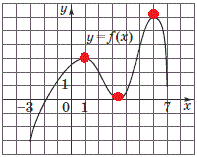
Ответ: В.
------------------------------
Задача 6. Какие из приведенных утверждений являются правильными ?
І. Через две прямые которые пересекаются можно провести только одну плоскость.
ІІ . Через точку не принадлежащую плоскости можно провести множество прямых параллельных к этой плоскости.
ІІІ . Если две различные плоскости параллельны одной и той же прямой то они параллельны между собой.
Варианты ответов:
А) только І,
Б) только І і ІІ,
В) только І і ІІІ,
Г) только ІІ і ІІІ,
Д) І, ІІ і ІІІ
Решение: По свойствам плоскостей выполняется только первое и второе утверждение, третье не верно, поскольку можно найти плоскости которые, будучи параллельными заданной прямой, между собой могут быть как параллельны так и пересекаться под любым углом.
Ответ: Б.
------------------------------
Задача 7. Решить уравнение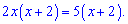 
Варианты ответов:
А) -2,5; 2
Б) -2
В) 2,5
Г) -2; 0,4
Д) -2; 2,5
Решение: Переносим все в левую часть и раскрываем скобки
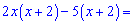
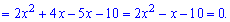
Получили квадратное уравнение которое решаем через дискриминант
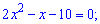
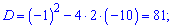
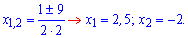
Из приведенных ответов справедлив только Д.
Ответ: Д.
------------------------------
Задача 8. Решить неравенство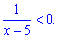 
Варианты ответов:
А)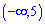 
Б)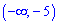 
В)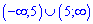 
Г)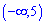 
Д)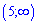 
Решение : Неравенства при тестировании даются легко не всем, поэтому при их решении нужно быть осторожными со знаками. В данном неравенстве числитель равен единице, а потому меньшим нуля может быть только знаменатель. Поэтому данное неравенство эквивалентно следующему
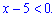
Переносим константу в правую сторону и получим решение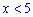 
или 
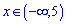что соответствует варианту А.
Ответ: А.
------------------------------
Задача 9. Если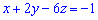 
и 
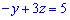то х=
Варианты ответов:
А) 9
Б) 11
В) 4
Г) -9
Д) -11
Решение: В этой задаче нужно увидеть что вторая часть находится в первой из множителем -2. Это легко заметить по самым выражениям, поэтому выполняем такие преобразования
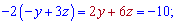
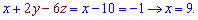
Ответ : Г.
------------------------------
Задача 10. На рисунке изображен график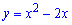 
.
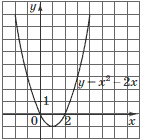
Укажите график функции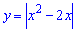 
.
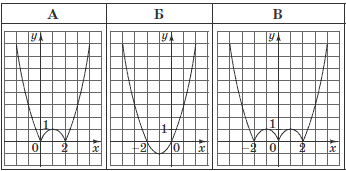
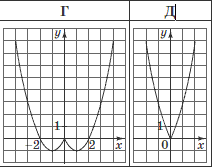
Решение: По свойству модуль функция отражает относительно оси Ох все что находится ниже. В результате получим что искомый график изображен на рисунке А. Также можно решить другим методом, подставив любую точку которая находится ниже оси абсцисс, например х=1, /y(1)/=1.
Отве: А.
------------------------------
Посмотрите ВНО математика. Решение задач № 11-16
