Характеристикой системы непрерывных случайных величин является плотность вероятностей. Для определения плотности вероятностей системы двух непрерывных случайных величин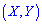 
применяется формула
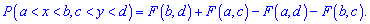
Рассмотрим прямоугольник со сторонами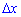 
и 
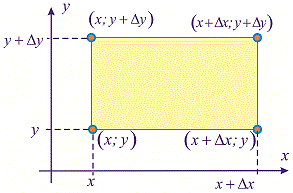
Вероятность размещения системы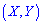 
в прямоугольной области вычисляется по формуле
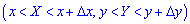
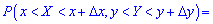
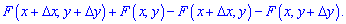
Разделив эту вероятность на площадь прямоугольника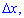 
и направив прирост аргумента к нулю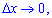 
получим вероятность в точке, то есть плотность:
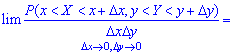
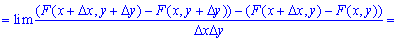
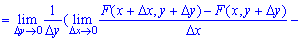
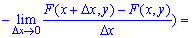
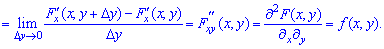
Итак, плотность распределения вероятностей системы двух случайных величин определяется зависимостью
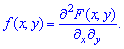
Функция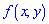 
может существовать только при условии, что функция распределения
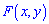является непрерывной по аргументам 
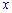и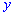 
и дважды дифференцируемой. Функции 
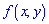в трехмерном пространстве соответствует определенная поверхность - так называемая поверхность распределения вероятностей системы двух непрерывных случайных величин 
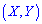. Тогда 
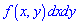— вероятность размещения системы двух случайных величин в прямоугольнике со сторонами 
.
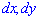Свойства плотности распределения вероятностей системы двух непрерывных случайных величин f (x, y)
1. 
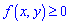является неотъемлемой функцией, поскольку 
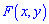является неубывающей относительно аргументов 
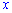и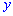 
.
2. Условие нормирования системы двух непрерывных случайных величин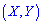 
такая:
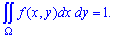
Если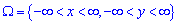 
, то приведенная условие принимает вид:
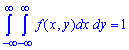
3.Вероятность размещения системы переменных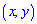 
в области 
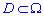вычисляется так:
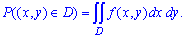
Вероятность размещения системы переменных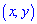 
в прямоугольной области 
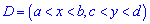определяется интегрированием
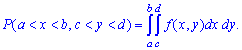
4. Функция распределения вероятностей системы двух переменных определяется из уравнения
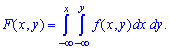
5. Если область задана прямоугольником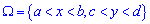 
, о функция распределения вероятностей имеет вид интеграла
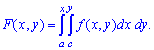
Рассмотрим следующий пример для закрепления материала.
-----------------------------------------
Задача. Дана поверхность распределения вероятностей для системы двух непрерывных случайных величин следующим законом:
функция является константой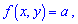 
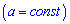, если аргументы относятся прямоугольной области 
;
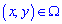и равна нулю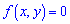 
вне его 
;
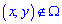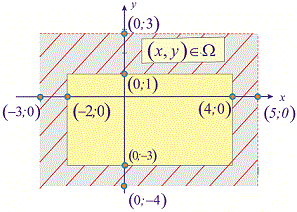
Прямоугольник задан областью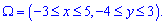 
Найти параметр 
и функция распределения вероятностей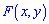 
. Вычислить вероятность попадания аргументов во внутренней прямоугольник ограничен областью
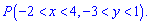
Решение. Прежде всего нарисуем прямоугольники, заданных условиями задачи. Это внесет некоторую ясность в процесс решения
Параметр 
определяем из условия нормировки:
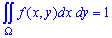
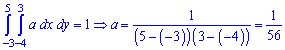
Таким образом, получили что поверхность распределения вероятностей системы двух непрерывных случайных величин равна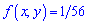 
для аргументов с прямоугольной области
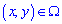и нулю 
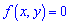вне ее 
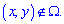Согласно 5 свойства в прямоугольнике 
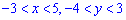определяем закон распределения вероятностей
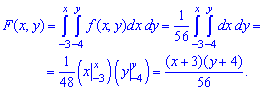
За его пределами функция принимает значения Аргументы принадлежат области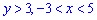 
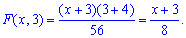
Если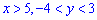 
, то имеем
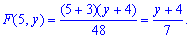
Для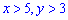 
функция равна
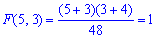
и при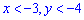 
принимает нулевое значение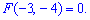 
На основе приведенных выше расчетов функция распределения вероятностей имеет вид
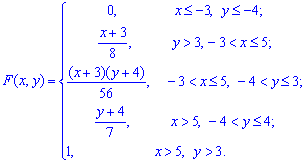
Вычисляем вероятность попадания аргументов во внутренней прямоугольник
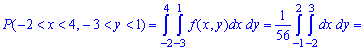
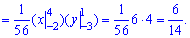
Полное отыскания функции распределения вероятностей достаточно частой задачей на практике и Вы должны уметь его выполнять. Для этого нужно интегрировать функцию плотности вероятностей. Таким образом изучая теорию вероятности - Вы на практике совершенствуете навыки интегрирования.
