Функцией распределения вероятностей системы двух случайных величин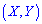 
называют такую функцию двух аргументов 
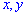, которая определяет вероятность совместное появления событий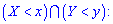
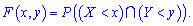
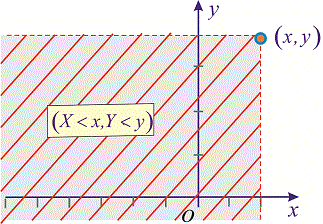
Проекция этой функции на плоскость изображена на рисунке
Свойства функции распределения вероятностей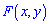 
1. Она принимает значения от нуля до единицы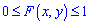 
, поскольку
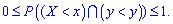
2. Если один из аргументов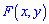 
стремится к бесконечности 
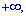то функция распределения системы стремится к функции распределения одного аргумента, не стремится к 
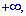а именно:
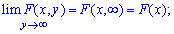
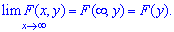
3. Если оба аргумента стремятся к бесконечности то значение функции в этих точках стремится к единице
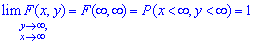
4. Если аргументы направляются к противоположному краю плоскости (минус бесконечности) то функция стремится к нулю
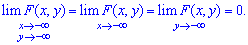
5. Функция распределения вероятностей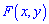 
является неубывающей функцией своих аргументов 
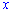и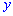 
.
6. Вероятность попаданий аргументов функции в прямоугольник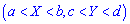 
вычисляется по формуле
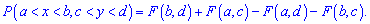
Рассмотрим задачу на последнее правило.
-----------------------------------------
Пример. Закон распределения системы двух непрерывных случайных величин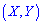 
задан функцией распределения вероятностей
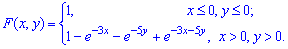
Вычислить вероятность попадания точки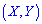 
в прямоугольник 
.
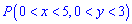Решение. Для полного представления прямоугольника попадания изобразим его графически
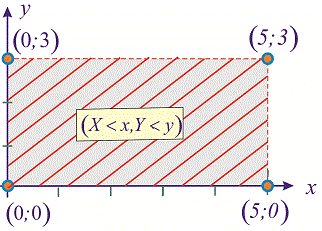
По правилу искомая вероятность определяется зависимостью
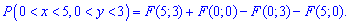
Вычислим составляющие
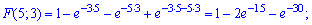
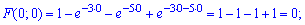
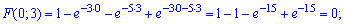
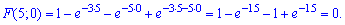
Последние три слагаемые можно было и не искать, с первого условия функции распределения
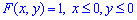
следует, что по осям она принимает нулевые значения.
Таким образом, искомая вероятность равна
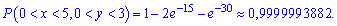
Графики функции распределения вероятностей приведены ниже
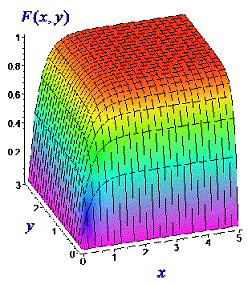
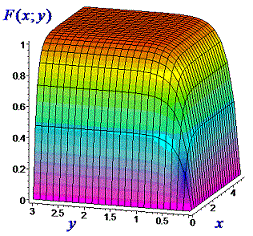
Они выполнены в среде Maple. В этой программе легко строить 3D графики и функция распределения вероятностей хорошо для этого подходит.
