Обобщенными числовыми характеристиками для случайных величин в теории вероятностей а также математической статистике являются начальные и центральные моменты. Задачи на отыскание моментов являются неотъемлемой частью теории вероятностей и математической статистики. Начальным моментом k-го порядка случайной величины Х называют математическое ожидание от величины в k-ой степени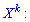 
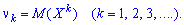
Когда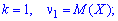 
Когда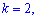 
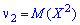и т. д.
Для дискретной случайной величины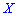 
начальные моменты определяют зависимостью
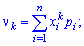
для непрерывной интегрированием
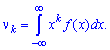
Если непрерывная величина задана интервалом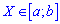 
, то моменты вычисляют по формуле
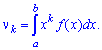
Центральным моментом k-го порядка называют математическое ожидание от величины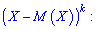 
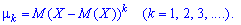
Когда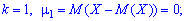 
для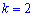 
имеем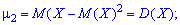 
при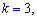 
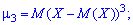
при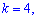 
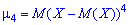
и так далее.
Для дискретной случайной величины центральные моменты вычисляют по формуле
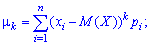
для непрерывной по следующей
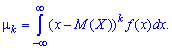
Если случайная величина определена интервалом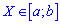 
, то центральные моменты определяют интегрированием
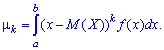
Рассмотрим пример отыскания приведенных величин.
-----------------------------------
Пример 1. Задана функция плотности вероятностей
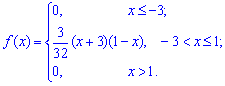
Вычислить начальные и центральные моменты второго и третьего порядка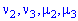 
.
Решение. Для вычисления начальных моментов выполним интегрирование по вышеприведенным формулам
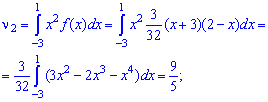
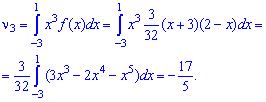
Промежуточные операции при интегрировании пропущены, они занимают много места, а Вам главное иметь инструкцию для вычислений, так как примеры у Вас будут другие.
Для вычисления центральных моментов инерции необходимо знать математическое ожидание случайной величины, поэтому определяем его первее
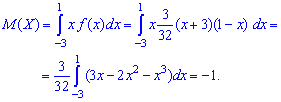
Найдено математическое ожидание подставляем в формулу центральных моментов. В случае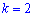 
получим
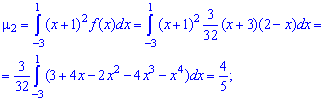
и при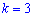 
будем иметь
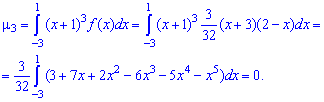
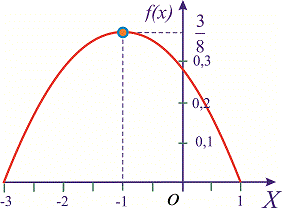
На этом решения примера завершено, функция плотности вероятностей приведена на графике
-----------------------------------
Примеры нахождения начальных и центральных моментов будут рассмотрены в следующей статье. Задачи совсем не сложные, а вычисления величин сводится к возведения в степень, интегрирование, умножение и суммирование.
