Математическое ожидание не дает достаточно полной информации о случайной величине, поскольку одному и тому же значению математического ожидания 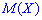 может соответствовать множество случайных величин, будут различаться не только возможными значениями, но и характером распределения и самой природой возможных значений.
может соответствовать множество случайных величин, будут различаться не только возможными значениями, но и характером распределения и самой природой возможных значений.
Например. Законы распределения двух случайных величин 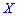 и
и 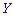 заданные таблицами:
заданные таблицами:

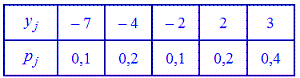
Вычислить математическое ожидание 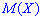 и
и 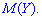
Решение. Находим математическое ожидание по класической формуле
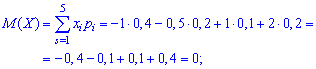
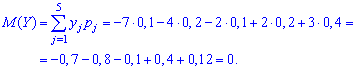
Получили, что для двух различных законов распределения математическое ожидание принимает одинаковое значения (0), при этом возможные значения случайных величин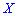 и
и 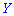 различаются. Из приведенного примера видно, что в случае равенства математических ожиданий
различаются. Из приведенного примера видно, что в случае равенства математических ожиданий 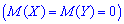 случайные величин
случайные величин 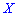 и
и 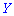 имеют тенденцию к колебаниям относительно
имеют тенденцию к колебаниям относительно 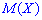 и
и 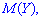 причем
причем 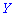 имеет больший размах рассеяния относительно
имеет больший размах рассеяния относительно 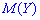 сравнительно случайной величине
сравнительно случайной величине 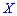 относительно
относительно 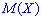 . Поэтому математическое ожидание еще называют центром рассеяния. Для определения рассеяния вводится числовая характеристика, называемая дисперсией.
. Поэтому математическое ожидание еще называют центром рассеяния. Для определения рассеяния вводится числовая характеристика, называемая дисперсией.
Для определения дисперсии рассматривается отклонение случайной величины 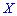 от своего математического ожидания
от своего математического ожидания 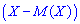
Математическое ожидание такого отклонения случайной величины 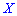 всегда равна нулю. В этом легко убедиться из следующего соотношения
всегда равна нулю. В этом легко убедиться из следующего соотношения
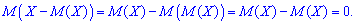
Таки образом, отклонение не может быть мерой рассеивания случайной величины.
Дисперсией случайной величины 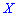 называют математическое ожидание квадрата отклонения случайной величины
называют математическое ожидание квадрата отклонения случайной величины 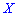 от своего математического ожидания
от своего математического ожидания 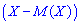
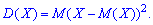
Для дискретной случайной величины 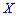 дисперсия вычисляется по формуле
дисперсия вычисляется по формуле
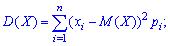
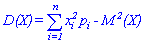
для непрерывной находят интегрированием
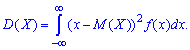
Если непрерывная величина заданная на интервале 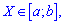 то дисперсия равна интегралу с постоянными пределами интегрирования
то дисперсия равна интегралу с постоянными пределами интегрирования
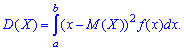
Дисперсия обладает следующими свойствами
1. Если случайная величина состоит из одной тотчки 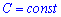 — постоянная величина, то дисперсия равна нулю
— постоянная величина, то дисперсия равна нулю
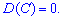
2. Дисперсия от произведения постоянной на случайную величину равна квадрату постоянной умноженной на дисперсию случайной величины
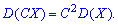
3. Если 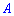 и
и  — постоянные величины, то для дисперсии
— постоянные величины, то для дисперсии 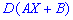 справедлива зависимость
справедлива зависимость
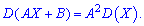
Это следует из двух предыдущих свойств.
Дисперсию можно вычислить по упрощенной формуле:
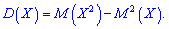
которая в случае дискретной случайной величины 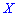 имеет вид
имеет вид
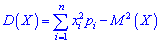
для непрерывной определяется зависимостью
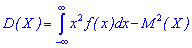
и для непрерывной на промежутке 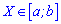 соотношением
соотношением
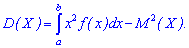
Приведенные формулы очень удобны в вычислениях, и их, в отличие от предыдущих, используют в обучении
Также следует помнить, что дисперсия всегда принимает неотрицательные значения 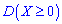 . Она характеризует рассеяние случайной величины относительно своего математического ожидания. Если случайная величина измерена в некоторых единицах, то дисперсия будет измеряться в этих же единицах, но в квадрате.
. Она характеризует рассеяние случайной величины относительно своего математического ожидания. Если случайная величина измерена в некоторых единицах, то дисперсия будет измеряться в этих же единицах, но в квадрате.
Для сравнения удобно пользоваться числовыми характеристиками одинаковой размерности случайной величиной. Для этого вводят в рассмотрение среднее квадратичное отклонение – корень квадратный из дисперсии. Ее обозначают греческой буквой «сигма»
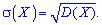
----------------------------------------
Рассмотрим примеры для ознакомления с практической стороной определения этих величин.
Пример 1. Закон распределения дискретной случайной величины 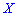 заданы таблицей:
заданы таблицей:

Вычислить дисперсию 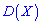 и среднее квадратическое отклонение
и среднее квадратическое отклонение 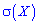 .
.
Решение. Согласно свойствами дисперсии получим:
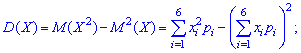
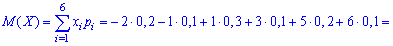
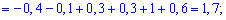
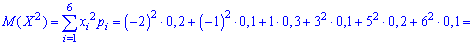
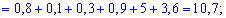
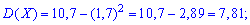
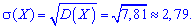
----------------------------------------
Пример2. Есть четыре электрические лампочки, каждая из которых имеет дефект с вероятностью 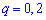 (
(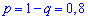 — вероятность того, что лампочка без дефекта). Последовательно берут по одной лампочке, вкручивают в патрон и включают электрический ток. При включении тока лампочка может перегореть, и ее заменяют на другую. Построить закон распределения дискретной случайной величины
— вероятность того, что лампочка без дефекта). Последовательно берут по одной лампочке, вкручивают в патрон и включают электрический ток. При включении тока лампочка может перегореть, и ее заменяют на другую. Построить закон распределения дискретной случайной величины 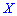 — число лампочек, которые будут опробованы. Вычислить среднее квадратическое отклонение
— число лампочек, которые будут опробованы. Вычислить среднее квадратическое отклонение 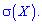
Решение. Дискретная случайная величина 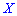 — число лампочек, которые будут опробованы - приобретает такие возможных значений:
— число лампочек, которые будут опробованы - приобретает такие возможных значений:
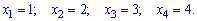
Вычислим соответствующие вероятности:
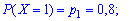
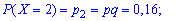
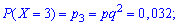
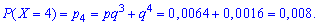
Последнюю вероятность можно трактовать следующим образом: четвертая лампочка будет испытана, когда третья перегорит, а четвертая - нет, или если и четвертая перегорит.
В табличной форме закон распределения  иметь следующий вид:
иметь следующий вид:
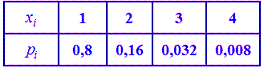
Для нахождения среднего квадратического отклонения найдем сначала значение дисперсии. Для дискретной случайной величины она примет значение:
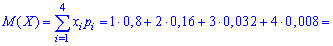
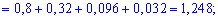
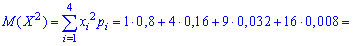
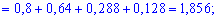
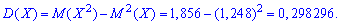
Среднее квадратичное отклонение находим добычей корня квадратного из дисперсии.
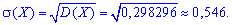
----------------------------------------
Пример 3. Закон распределения вероятностей дискретной случайной величины  заданы в виде функции
заданы в виде функции
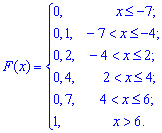
Вычислить среднее квадратическое отклонение и дисперсию 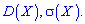
Решение. С помощью функции распределения вероятностей формируем закон распределения в виде таблицы
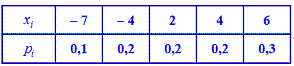
На основе таблицы распределения вычисляем дисперсию
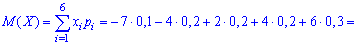
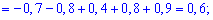
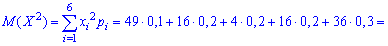
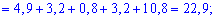
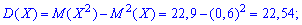
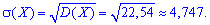
-----------------------
Подобных примеров можно привести множество, основная их суть в правильном применении приведенных в начале статьи формул для вычисления дисперсии и математического ожидания. Применяйте их там где это необходимо и не допускайте ошибок при определении дисперсии.


