Асимметрия, эксцесс. Вычисление

Вычисление асимметрии и эксцесса позволяет установить симметричность распределения случайной величины 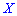относительно 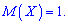Для этого находят третий центральный момент, характеризующий асимметрию закона распределения случайной величины. Если он равен нулю 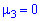, то случайная величина 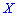симметрично распределена относительно математического ожидания 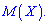Поскольку 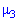имеет размерность случайной величины в кубе, то вводят безразмерную величину — коэффициент асимметрии:

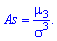
Центральный момент четвертого порядка используется для определения эксцесса, характеризует плосковершиннисть или гостровершиннисть плотности вероятности 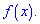Эксцесс вычисляется по формуле

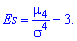
Число 3 вычитается для сравнения отклонения от центрального закона распределения (нормального закона), для которого подтверждается равенство:

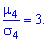
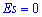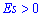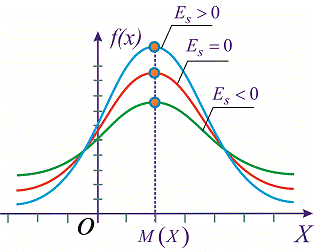
Итак, для нормального закона распределения. Если эксцесс положительный то на графике функция распределения остро вершину и для отрицательных значений более пологую. Таким образом можно установить отклонения заданного закона от нормального. Для наглядности при различных значениях асимметрии и эксцесса графики плотности вероятностей изображены на рисунках ниже

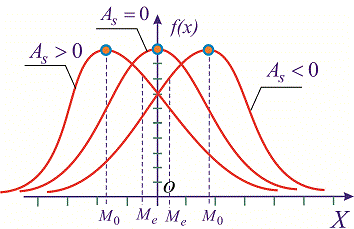
Приведу Вам один из распространенных примеров.

Пример 1. Дана плотность вероятностей:

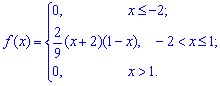
Вычислить асимметрию и эксцесс .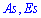

Решение. Вычисляем математическое ожидание случайной величины

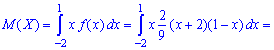
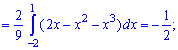
после этого - третий момент инерции

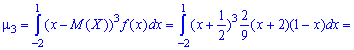
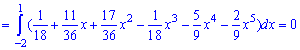
Поскольку момент нулевой 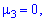то и асимметрия равна нулю 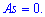.Следовательно, возможные значения случайной величины 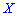симметрично распределены относительно единицы 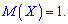. Для вычисления эксцесса 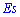необходимо найти четвертый момент 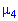и среднее квадратическое отклонение. .

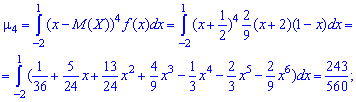
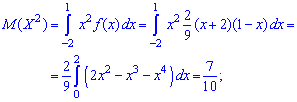
По найденным значениям вычисляем дисперсию

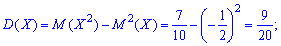
после нее среднее матиматичне отклонения

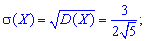
Окончательно получим

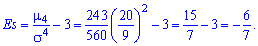
отрицательный эксцесс, что указывает на пологость функции распределения. Сам график функции с найденными величинами приведен на рисунку ниже

--------------------------------------

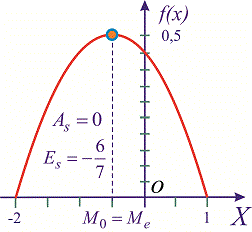
Хорошо разберите приведенный пример, все другие подобные. Найти асимметрию и эксцесс довольно легко тем, кто хорошо умеет интегрировать и не спешит при вычислениях.