Метод Гаусса заключается в последовательном исключении переменных и преобразовании системы линейных алгебраических уравнений
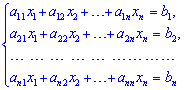
к треугольному виду
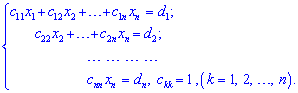
Предположим, что в системе коэффициент 
. Если это условие не выполняется, то на первое место переносим уравнение, которое ее удовлетворяет. С помощью первого уравнения исключим 
из остальных уравнений.
Для этого делят первую строчку на 
, обозначим
.
Дальше второй строки вычитаем первую строку, умноженную на 
;от третьего первую строчку, умноженный на 
; и так далее до последней строки. Получим таблицу коэффициентов:
Для неизвестных 
имеем систему 
уравнений. Выполняя, как и раньше, исключим 
из всех уравнений, начиная с третьего. Для этого сначала разделим вторую строчку на 
.
Если коэффициент 
, то переставим уравнения так, чтобы выполнялось условие 
.
Обозначив
,
от третьей строки вычтем вторую строчку, умноженный на 
;
от четвертой строки вычтем вторую строчку, умноженный на 
и т.д. Получим таблицу коэффициентов:
Продолжая процесс исключения неизвестных получим таблицу:
Таблица коэффициентов при неизвестных сводится к треугольному виду. Все главной диагонали элементы 
. Запишем соответствующую систему уравнений:
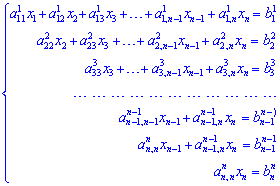
Переход от первой системы уравнений до последней называется прямым ходом метода Гаусса. Обратный ход метода Гаусса начинается с последней системы уравнений. Ее решают с конца до начала. Из последнего уравнения находят 
. Подставив это значение в предпоследнее - находят 
и т.д. Из первого уравнения находят 
.
Если система уравнений с неизвестными имеет единственное решение, то эта система всегда может быть преобразована к треугольному виду. Для студентов не всегда требуют, чтобы диагональные элементы были равны единице. Достаточно просто свести систему линейных уравнений к верхней треугольной.
--------------------------------------------
Пример 1.
Дана система трех линейных уравнений с тремя неизвестными. Решить систему методом Гаусса.
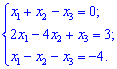
Решение.
Исключим неизвестную 
из второго и третьего уравнения. Для этого от них вычтем первое умноженное на 
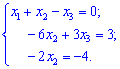
Видим, что наше уравнение в таком виде можно решать обратным ходом метода Гаусса. Для этого из последнего уравнения выразим 
Подставим полученное значение в предыдущее уравнение и найдем 
Из первого уравнения находим 
Решение данной системы равен 
-----------------------------------------
В случаях систем больших размеров, а также для удобства, часто на практике используют другую схему решения. Вместо преобразований над системой выполняют соответствующие преобразования над матрицей, составленной из коэффициентов при неизвестных и столбца из свободных членов, который для удобства выделяют вертикальной линией. Такую матрицу 
называют расширенной матрицей системы.
-----------------------------------------
Пример 2.
Решить систему четырех линейных алгебраических уравнений методом Гаусса.
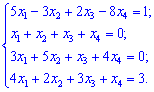
Решение.
Выпишем расширенную матрицу для данной системы
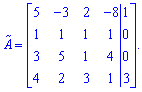
Сведем ее к треугольному виду с помощью элементарных преобразований.
1.Поменяем местами первый и второй строки.
2. Добавим к элементам второго, третьего и четвертого строк элементы первой строки, умноженные соответственно на 
3. Поменяем местами второй и третий строки. Добавим к элементам третьего и четвертого строк элементы второй строки, умноженные соответственно на 
4. От четвертого уравнения умноженного на 
вычитаем третье уравнение умноженное на 
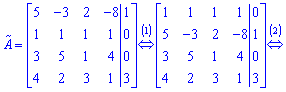
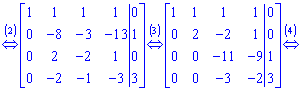
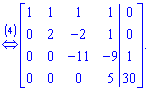
Такой расширенной матрицы соответствует следующая система уравнений
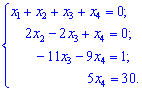
С четвертого уравнения находим 
и подставляем в третье уравнение
Найденные значения подставляем во второе уравнение
Из первого уравнения находим первую неизвестную
Система полностью решена и 
– ее решение.
-----------------------------------------------------
Посмотреть материалы:
