Задачи на вычисление значения функций в окрестности нуля, или иной точки очень важны в математике и без специальных калькуляторов или программ найти их значение трудно. В помощь студентам, инженерам и другим специалистам приходят ряды Тейлора. Функцию раскладывают в ряд, отбирают несколько первых членов, которые вносят наибольший вклад и обеспечивают достаточную точность вычислений. После этого находят значение в заданной точке.
Рассмотрим примеры применений рядов Тейлора к приближенным вычислениям.
--------------------------------------------
Пример 1. Вычислить с точностью до 0,0001
1) 
2) (9.331) 
3) (9.333) 
4) (9.333)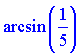 
Решение. 1) Запишем заданную функцию в удобном виде
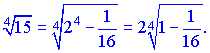
Воспользуемся формулой разложения в ряд Тейлора
и выпишем несколько членов ряда при степенях аргумента
В результате получим значение
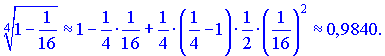
Согласно записанной выше формуле, умножаем полученное число на 2
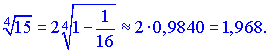
2)
Воспользуемся разложением синус функции в окрестности нуля
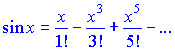
Заданное выражение перепишем в следующей форме
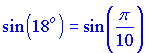
и подставим в формулу
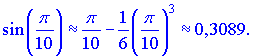
Взяв только два члена ряда получаем достаточно хорошую сходимость. И такая сходимость бывает не всегда. Чем дальше отдаляемся от точки в которой развит ряд, тем больше членов разложения нужно брать для точности результата.
3)
Выпишем разложение логарифма около единицы
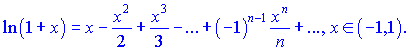
В данном случае подставим 
и просуммируем несколько членов ряда
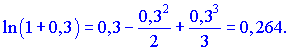
Точный результат равный
Для обеспечения сходимости с точностью 0,0001 нужно брать больше членов ряда
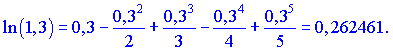
Получили хорошую сходимость, но пришлось брать пять членов разложения в ряд. Это связано с тем что точка в которой искали приближенное значение находится далеко от точки разложения ряда.
4)
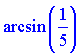
Пусть имеем разложение арксинуса возле нуля
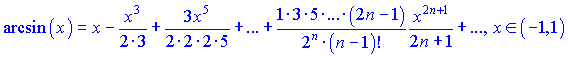
Точное значение будет следующим
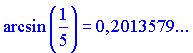
Взяв два члена ряда
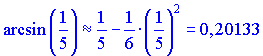
получим хорошую сходимость.
По аналогии с прведенными примерами поступаем и для ряда других функций.
