Как найти обратную матрицу подробно описано в предыдущих уроках. Напомню лишь последовательность вычислений:
- находим определитель главной матрицы;
- дальше вычисляем алгебраические дополнения к матрице;
- последним шагом нужно транспонировать матрицу алгебраических дополнений и разделить на определитель.
Результатом вычислений и будет обратная матрица.
Ниже приведены примеры пошагового вычисления матрицы 3х3.
Пример 1. Найти обратную матрицу
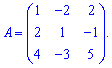
Решение: Вычисляем определитель матрицы 3 * 3 по правилу треугольников
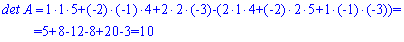
Определитель отличен от нуля, следовательно матрица А не вырожденная и существует обратная к ней.
Алгебраические дополнения равны минорам умноженным на (-1) в степени суммы номера строки и столбца элемента матрицы.
Для простоты можно использовать приведенную ниже схему знаков миноров
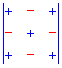
Миноры равны определителю на единицу меньшего порядка чем матрица и образуются вычеркиванием строки и столбца на пересечении которых находится элемент.
Более понятно станет с вычислений алгебраических дополнений
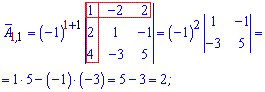
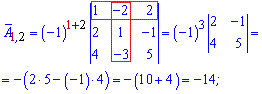
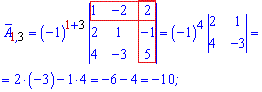
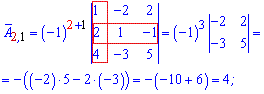
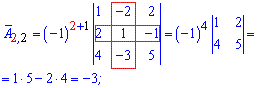
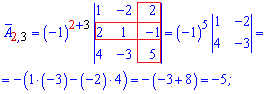
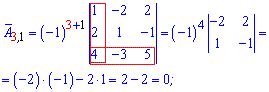
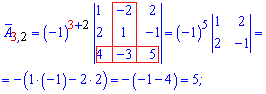
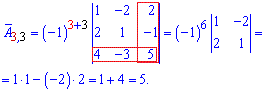
Из найденных значений выписываем матрицу алгебраических дополнений
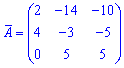
Транспонирует ее чтобы получить присоединенную (союзное) матрицу
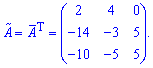
На этом этапе будьте внимательны - можно выполнить правильно приведенные выше вычисления и из-за неумения транспонировать получить неверный результат.
Делим на определитель и получаем обратную матрицу
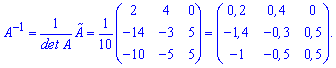
Найти обратную матрицу Вам поможет калькулятор обратной матрицы YukhymCalc. Для этого заходите в меню калькулятора и выбираете вычисления обратных матриц
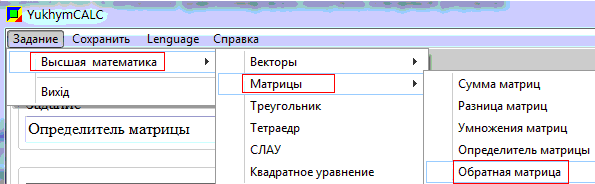
Далее задаете размер матрицы
и вводить элементы матрицы.
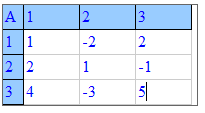
После вычислений Вы получите элементы матрицы дополнений
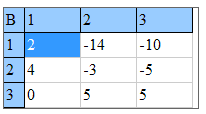
союзной матрицы, и обратной, а также определитель.
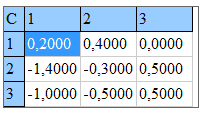
Все действия расписаны подробно в отдельном окне

и результаты вычислений можно сохранить в текстовый файл

Используйте калькулятор для нахождения обратной матрицы и проверки правильности вычислений.
Пример 2. Найти обратную матрицу
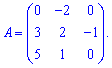
Решение: Вычисляем определитель матрицы разложив его по первой строке. Это довольно удобно так как имеем два элемента которые равны нулю
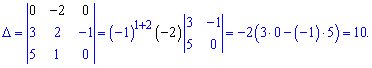
Алгебраические дополнения находим воспользовавшись приведенной выше схемой знаков миноров
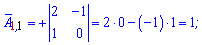
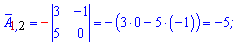
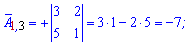
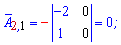
Если в определителе строка или столбец содержит элементы = 0 то он равен 0.
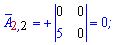
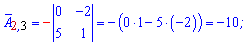
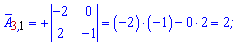
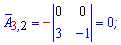
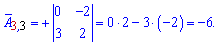
Записываем матрицу алгебраических дополнений
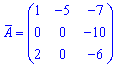
Присоединенную матрицу находим транспонированием найденной
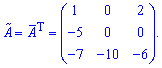
Находим обратную матрицу по известной формуле
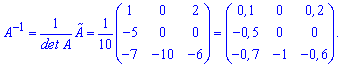
Калькулятор обратной матрицы дает следующий результат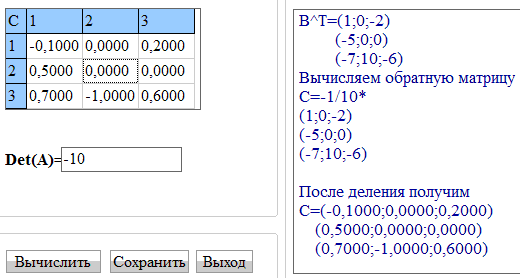
Сравнением убеждаемся что обратную матрицу найдено правильно. Используйте приведенную методику в обучении и с опытом у Вас не будет проблем с обратной матрицей.


