Геометрическая прогрессия не менее важная в математике по сравнению с арифметической. Геометрической прогрессией называют такую последовательность чисел b1, b2,..., b[n] каждый следующий член которой, получается умножением предыдущего на постоянное число. Это число, которое также характеризует скорость роста или убывания прогрессии называют знаменателем геометрической прогрессии и обозначают
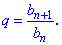
Для полного задания геометрической прогрессии кроме знаменателя необходимо знать или определить первый ее член. Для положительного значения знаменателя 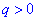 прогрессия является монотонной последовательностью, причем если
прогрессия является монотонной последовательностью, причем если 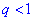 это последовательность чисел является монотонно убывающей и при
это последовательность чисел является монотонно убывающей и при 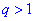 монотонно возрастающей. Случай, когда знаменатель равен единице
монотонно возрастающей. Случай, когда знаменатель равен единице 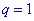 на практике не рассматривается, поскольку имеем последовательность одинаковых чисел, а их суммирование не вызывает практического интереса
на практике не рассматривается, поскольку имеем последовательность одинаковых чисел, а их суммирование не вызывает практического интереса
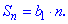
Общий член геометрической прогрессии вычисляют по формуле
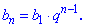
Сумма n первых членов геометрической прогрессии определяют по формуле
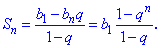
Рассмотрим решения классических задач на геометрическую прогрессию. Начнем для понимания с простейших.
Пример 1. Первый член геометрической прогрессии равен 27, а ее знаменатель равен 1/3. Найти шесть первых членов геометрической прогрессии.
Решение: Запишем условие задачи в виде
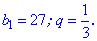
Для вычислений используем формулу n-го члена геометрической прогрессии
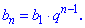
На ее основе находим неизвестные члены прогрессии
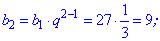
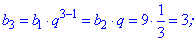
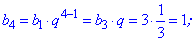
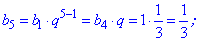
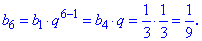
Как можно убедиться, вычисления членов геометрической прогрессии несложные. Сама прогрессия будет выглядеть следующим образом
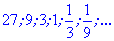
Пример 2. Даны три первых члена геометрической прогрессии 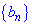 : 6; -12; 24. Найти знаменатель и седьмой ее член.
: 6; -12; 24. Найти знаменатель и седьмой ее член.
Решение: Вычисляем знаменатель геомитрической прогрессии исходя из его определения
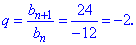
Получили знакопеременную геометрическую прогрессию знаменатель которой равен -2. Седьмой член вычисляем по формуле
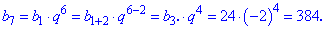
На этом задача решена.
Пример 3. Геометрическая прогрессия 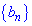 задана двумя ее членами
задана двумя ее членами 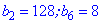 . Найти десятый член прогрессии.
. Найти десятый член прогрессии.
Решение:
Запишем заданные значения через формулы
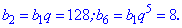
По правилам нужно было бы найти знаменатель, а затем искать нужное значение, но для десятого члена имеем
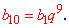
Такую же формулу можно получить на основе нехитрых манипуляций с входными данными. Разделим шестой член ряда на другой, в результате получим
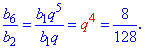
Если полученное значение умножить на шестой член, получим десятый
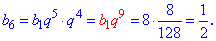
Таким образом, для подобных задач с помощью несложных преобразований в быстрый способ можно отыскать правильное решение.
Пример 4. Геометрическая прогрессия задано рекуррентными формулами
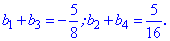
Найти знаменатель геометрической прогрессии и сумму первых шести членов.
Решение:
Запишем заданные данные в виде системы уравнений
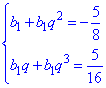
Выразим знаменатель разделив второе уравнение на первое
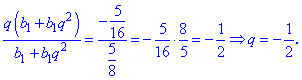
Найдем первый член прогрессии из первого уравнения
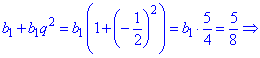
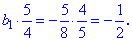
Вычислим следующие пять членов для нахождения суммы геометрической прогрессии
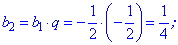
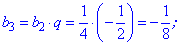
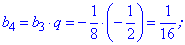
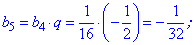
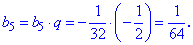
Поскольку найти сумму в данном случае не составляет большого труда, то обходя простые выкладки сводим все слагаемые под общий знаменатель
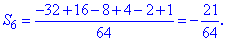
В общем случае, при нахождении суммы знакопеременных рядов следует выделять их положительную часть и отрицательную и найти отдельно их суммы по приведенным выше формулам. Наконец найденные значения добавить.
Примеры на геометрическую прогрессию не так сложны если знать несколько базовых формул. Все остальное сводится к простым математическим манипуляциям. Практикуйте с примерами самостоятельно и подобные задания будут для Вас несложными.
Похожие материалы:


