В настоящей статье научимся вычислять криволинейный интеграл от полного дифференциала.
Схема решения:
- сначала нужно убедиться, что подынтегральная функция является полным дифференциалом
- дальше найти интеграл между заданными точками.
Формула Ньютона-Лейбница для криволинейного интеграла от полного дифференциала
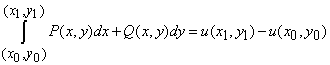
Криволинейный интеграл имеет одно полезное для вычислений свойство, он не зависит от формы кривой, по которой интегрируем.
Поэтому вместо интегрировать по прямой между двумя точками строят ломаную параллельно осям координат и интегрируют по ней.
За счет этого один из дифференциалов в интеграле превращается в нуль, таким образом упрощаются вычисления.
Детальнее алгоритм проверки подынтегрального выражения на полный дифференциал и вычисление криволинейных интегралов приведены в следующих 6 примерах.
Пример 1 Убедившись, что подынтегральное выражение является полным дифференциалом, вычислить криволинейный интеграл int[(x+y)dx+(x-y)dy]
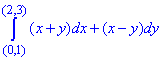
Решение: Подынтегральные функции являются первобытными для полного дифференциала
(x+y)dx+(x-y)dy.
Выпишем P=P(x, y)=x+y, Q=Q(x, y)=x-y.
но найдем частичные производные первого порядка функций P(x, y) и Q(x, y):
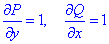
Сравнением убеждаемся, что частичные производные равны
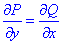
поэтому подынтегральное выражение (x+y)dx+(x-y)dy является полным дифференциалом.
Криволинейный интеграл от точки (0,1) к точке (2,3) будем вычислять вдоль прямых y=1 и x=2.
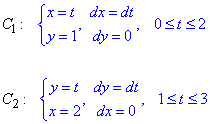
Так верно выполнять, поскольку на каждом интервале один из дифференциалов равен нулю, следовательно, интеграл упрощается.
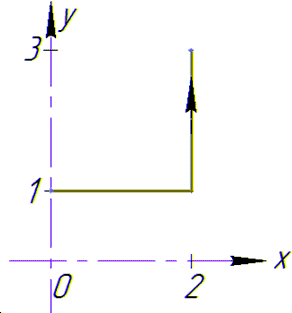
Вычислим заданный криволинейный интеграл:
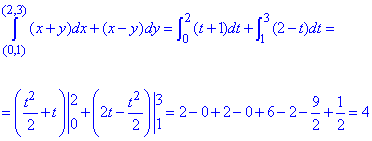
Пример 2 Убедившись, что подынтегральное выражение является полным дифференциалом, вычислить криволинейный интеграл
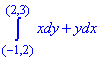
Решение: Имеем подынтегральное выражение:
xdy+ydx.
Выпишем значение при дифференциалах
P=P(x, y)=y, Q=Q(x, y)=x.
Найдем частичные производные первого порядка функций P, Q:
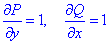
Сравнением значений убеждаемся, что подынтегральное выражение является полным дифференциалом.
Заданный криволинейный интеграл от точки (- 1,2) к точке (2,3) будем вычислять вдоль прямых y=2 и x=2.
На графике направление и контур интегрирования имеют вид
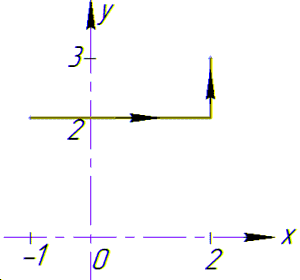
Выпишем как буду изменяться координаты и дифференциалы на каждом интервале
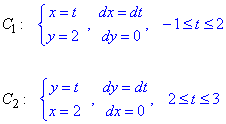
Найдем криволинейный интеграл через сумму двух:
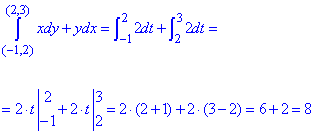
Пример 3 Убедившись, что подынтегральное выражение является полным дифференциалом, вычислить криволинейный интеграл
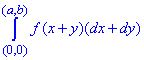
где f(u) непрерывная функция.
Решение: Выписываем подынтегральное выражение:
f(x+y)(dx+dy)=f(x+y)dx+f(x+y)dy.
Отсюда P=P(x, y)=f(x+y), Q=Q(x, y)=f(x+y).
Поскольку P, Q симметрично содержат переменные, то их частичные производные
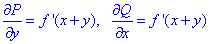
равны, а это значит что подынтегральное выражение является полным дифференциалом.
Криволинейный интеграл от точки (0,0) к точке (a, b) будем вычислять вдоль прямых y=0 и x=a.
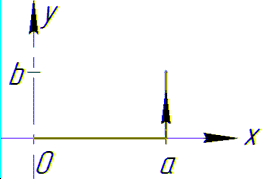
Выпишем пределы интеграла и дифференциалы
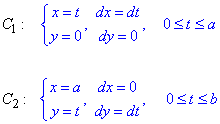
Криволинейный интеграл упрощаем с помощью замены переменных:
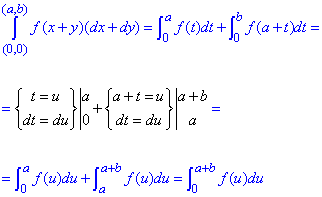
здесь f(u) заданная непрерывная функция.
Пример 4 Убедившись, что подынтегральное выражение является полным дифференциалом, вычислить криволинейный интеграл
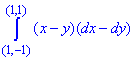
Решение: Подынтегральное выражение
(x-y)dx-(x-y)dy.
Дальше функции P=P(x, y)=x-y; P=P(x, y)=-x+y.
Найдем частичные производные от P, Q:
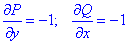
Мешаные производные равны
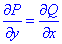
поэтому подынтегральное выражение является полным дифференциалом.
Криволинейный интеграл от точки (1, -1) к точке (1,1) будем вычислять вдоль прямой x=1.
В прямоугольной СК контур интегрирования имеет вид
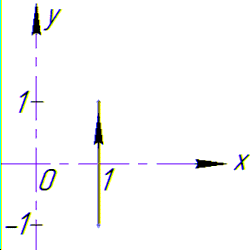
Здесь имеем лишь один промежуток интегрирования
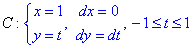
Вычислим заданный криволинейный интеграл:
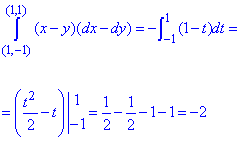
Пример 5 Убедившись, что подынтегральное выражение является полным дифференциалом, вычислить криволинейный интеграл
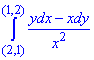
вдоль путей, которые не пересекают ось Oy.
Решение: Имеем подынтегральное выражение:
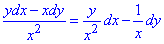
Отсюда P=P(x, y)=y/x2, Q=Q(x, y)=-1/x.
Вычислим частичные производные функций P(x, y), Q(x, y):
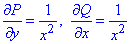
они равны между собой, поэтому подынтегральное выражение является полным дифференциалом.
Криволинейный интеграл от точки (2,1) к точке (1,2) будем вычислять вдоль прямых x=2 и y=2.
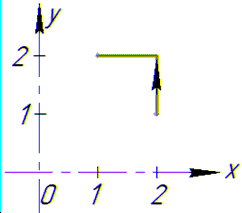
Запишем диапазон изменения пределов интеграла и дифференциалы
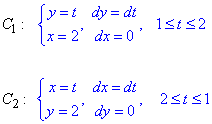
Вычислим заданный криволинейный интеграл:
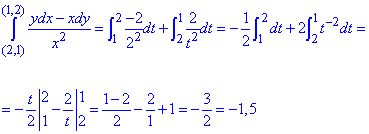
Пример 6 Убедившись, что подынтегральное выражение является полным дифференциалом, вычислить криволинейный интеграл
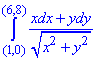
вдоль кривых, что не проходят через начала координат.
Решение: Подынтегральное выражение разобьем на сумму двух:
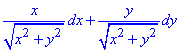
Выписываем производные при дифференциалах
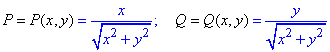
Найдем частичные производные первого порядка функций P, Q:
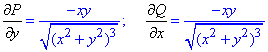
Сравнением значений делаем вывод что имеем полный дифференциал под интегралом.
Заданный криволинейный интеграл от точки (1,0) к точке (6,8) будем вычислять вдоль прямых y=0 и x=6, то есть на двух интервалах
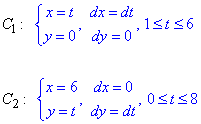
В декартовой плоскости контур интегрирования имеет вид
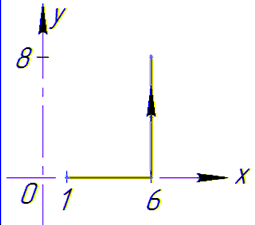
Криволинейный интеграл равен 9
Приведенных примеров на вычисление криволинейного интеграла от полного дифференциала вполне достаточно, чтобы выучить алгоритм проверки подынтегральной функции на полный дифференциал.
Разбивать участок между точками на промежутки параллельные осям тоже не трудно.
Интегрировать Вы должны уметь хорошо прежде чем браться за подобные примеры.
Если имеете трудности в интегрировании обращайтесь к нам за помощью, думаю, договоримся!


