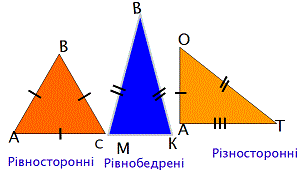
Для усвоения и повторения материала за 5-6 класс темы "треугольники" напомним их классификацию.
В зависимости от значения углов треугольники делятся на :
- остроугольные;
- прямоугольные;
- тупоугольные.
 В зависимости от длины сторон треугольники делятся на
В зависимости от длины сторон треугольники делятся на
- равносторонние;
- равнобедренные;
- разносторонние.
Основные признаки равнобедренного треугольника
1. Если имеем треугольник в котором два угла равны, то он равнобедренный.
2. Треугольник равнобедренный, если:
- одна из его высот является медианой;
- одна из его медиан является биссектрисой;
- одна из его высот является биссектрисой.
3. Треугольник равнобедренный, если:
- две его высоты равны;
- две его медианы равны;
- две его биссектрисы равны.
Начинают изучать треугольники в 5-7 классе в курсе геометрии школьной программы с простых заданий на усвоение определения равнобедренного треугольника, а также на стороны и углы треугольника. Для примера, "Определить углы при основании, если угол при вершине равен 110 градусов". 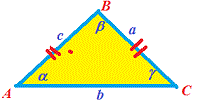
Вычисления таких задач проще простого. Сумма углов треугольника равна 180 градусов, углы при основании (beta) равны. Отсюда на все случаи углов при вершине alpha следует применять формулу
beta=(180-alpha)/2.
Если угол при вершине 110 градусов, то у основания равнобедренного треугольника углы равны
beta=(180-110)/2=35 (градусов).
Пусть задан угол при основании равнобедренного треугольника и он равен 50 градусов, тогда угол при вершине равен
alpha=180-2*50=80 (градусов).
Меняете в формуле значения угла (50) на свой и находите угол в вершине треугольника для любого равнобедренного треугольника.
По мере изучения свойств треугольника, формулы для вписанных и описанных окружностей, возрастает и сложность вычислений и разнообразие задач, которые можно решить. Таким образом в 8-9 классе задачи на треугольники требуют знаний немало важных формул без которых вычисления невозможно выполнить.
Распространенные и самые простые формулы – это периметр и площадь равнобедренного треугольника. Тут никакие свойства треугольника не упрощают указанных величин и их находим по общим формулам треугольника
p=a+b+c;
S=1/2*a*h – площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне. Вторая распространенная формула применяется, если известны стороны и угол между ними.
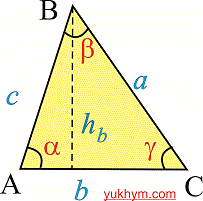
Тогда площадь треугольника равна половине произведения сторон на синус угла между ними. Согласно приведенному рисунку имеем
S=1/2*a*b*sin(hamma);
S=1/2*b*c*sin(alpha);
S=1/2*a*c*sin(beta).
Если задана одна из равных сторон a=b и угол при вершине, то площадь равна
S=1/2*a*a*sin(hamma).
Примеры на равнобедренный треугольник
Часть примеров, что приведены ниже можно назвать устными, поскольку соображения для объяснения вычислений или доказательств можно выполнить в голове без применения ручки и тетради.
Пример 1Является ли равнобедренным любой равносторонний треугольник?
Является ли равносторонним любой равнобедренный треугольник?
Ответ: Любой равносторонний треугольник всегда будет равнобедренным. А вот обратное утверждение не верно. Не все равнобедренные треугольники являются равносторонними, а лишь такие, в которых все стороны или углы равны.
Пример 2. В треугольнике ABC стороны AB=BC равны. Назовите равные углы треугольника.
Ответ: Общей для сторон является вершина В, следовательно, углы при других основаниях равны между собой ∠A=∠C.
Пример 3. Угол между высотой и стороной равнобедренного треугольника равен 30 градусов. Найти угол при основании.
Решение: Поскольку в равнобедренном треугольнике высота является одновременно биссектрисой, то полный угол при вершине равен заданному, умноженному на 2
beta=2*30=60 (градусов).
Вычисляем угол при основании треугольника
alpha=(180-60)/2=60 (градусов).
Поскольку все углы при вершинах треугольника равны, то заданный треугольник является равносторонним.
Пример 4. Какими углами при основании должен обладать треугольник, чтобы он был одновременно и равнобедренным и прямоугольным?
Решение: Прямоугольный треугольник имеет прямой угол (90 градусов) – это знают все. Найдем углы при основании по формуле
alpha=(180-90)/2=45 (градусов).
Таким образом равнобедренный прямоугольный треугольник должен иметь углы 45, 45, 90 градусов.
Пример 5. Высота равнобедренного треугольника равна половине основания. Найти угол при основании треугольника.
Решение: Поскольку высота перпендикулярна основанию и равна ее половине, то угол между основанием и высотой и высотой и стороной равны между собой и составляют 45 градусов. Если Вам это трудно осознать, то приучите себя выполнять построение к условию задания. Многим это помогает быстрее усвоить материал.
Пример 6. Периметр равнобедренного треугольника равен 2,6 м. Найдите стороны треугольника, если его основание больше боковой стороны на 0,5 м.
Решение: В такого типа заданиях нужно составить уравнение. Обозначим сторону треугольника через t. Тогда основание по условию равно
t+0,5 м.
Составляем уравнение для вычисления стороны треугольника
t+t+t+0,5=2,6;
3*t=2,6-0,5=2,1;
t=2,1/3=0,7 (м).
Пример 7. Периметр равнобедренного треугольника равен 20 см.
Найдите:
а) основание треугольника, если его боковая сторона равна 7,5 см;
б) боковую сторону треугольника, если его основание равно 4 см;
в) стороны треугольника, если его боковая сторона относится к основанию как 3:4.
Решение: a) Для вычисления основания из периметра вычтем равные стороны
b=20-2*7,5=6 (см).
б) Найдем боковую сторону равнобедренного треугольника по формуле
a=(20-4)/2=8 (см).
в) Согласно пропорции между стороной и основанием равнобедренного треугольника введем обозначения
сторона равна - 3*Х;
Тогда основание - 4*Х.
Составляем уравнение периметра
3*Х+3*Х+4*Х=20;
10*X=20;
X=20/10=2 (cм).
Вычисляем стороны треугольника
3*2=6 (см)
4*2=8 (см).
Стороны треугольника равны 6, 6, 8 см.
Пример 8. Периметр равнобедренного треугольника ABC равен 18 см, причем основание AC меньше боковой стороны на 3 см. Найдите основание треугольника ABC
Решение: Вводим обозначения: основание – Х, сторона Х+3.
Составляем уравнение
Х+2*(Х+3)=18;
3*Х=18-6=12;
Х=12.3=4 (см).
Ответ: основание треугольника равна 4 см
Задачи на площадь треугольника
Задача 1. Стороны равнобедренного треугольника 5 см, основание – 6 см Найдите площадь треугольника .
Решение: Сначала выполняем построение к задаче. 
Для вычисления площади нам кроме основы нужно найти высоту треугольника. Известно, что высота является медианой равнобедренного треугольника, то есть делит основание на два отрезка по 6/2=3 (см). Далее вычисляем высоту ка катет прямоугольного треугольника
h^2=5^2-3^2=25-9=16;
h=sqrt(16)=4 (см).
Вычисляем площадь треугольника
S=1/2*6*4=12 (сантиметров квадратных).
Ответ: 12.
Задача 2. Стороны равнобедренного треугольника 10 см, а высота опущенная к основанию – 8 см. Найдите площадь треугольника .
Решение: Построим треугольник. Половину стороны основания обозначим через x. По теореме Пифагора составим уравнение
8^2+x^2=10^2;
x^2=100-64=36;
x=6 (см).
Полное основание в два раза больше – 12 см. Находим площадь треугольника
S=12*8/2= 48 (сантиметров квадратных).
Задача 3. Стороны равнобедренного треугольника равны 5, 5, 6 см. Найти радиус окружности описанной вокруг треугольника.
Решение Для вычисления радиуса описанной вокруг треугольника окружности необходимо знать формулу
Поскольку стороны известны то площадь можем найти через формулу Герона, однако это сложный путь. Проще по теореме Пифагора найти высоту треугольника. Поскольку высота является перпендикуляром к основанию и, одновременно медианой, то высота равна катету прямоугольного треугольника с гипотенузой 5 см и катетом
6/2=3 см .
Вычисляем высоту

 (см).
(см).
Находим площадь треугольника
S=1/2*6*4=12 (см. кв.).
Имеем все данные для вычисления радиуса окружности
R=5*5*6/12=12,5 (см).
Ответ: радиус окружности равен 12,5 см.
В интернете немало примеров на равнобедренный треугольник. Часть из них похожи к рассмотренным задачам, другие - более сложные и требуют применения большего количества формул. Свойства равнобедренного треугольника часто встречаются в задачах на ромб, пирамиду, трапеции. Поэтому, изучив базовые формулы и правила на простых фигурах, на сложных применять знания становится намного проще.
]]>Ниже приведены готовые ответы распространенных на практике примеров, которые подобраны из сборников тестов и школьных учебников. Не рассмотренными в статье остались примеры с множеством вычислений, как, например, применение формулы Герона, или нахождение определенных геометрических размеров. В скором времени и они будут подробно расписаны и объяснены.
Задача 1 Основа равнобедренного треугольника равна 24 см. Найдите радиус окружности, вписанной в треугольник, если проведенная к основанию высота равна 16 см.
Решение: Из курса геометрии известно, что радиус вписанной в треугольник окружности равен отношению его площади к полупериметру. Осталось найти значения двух последних величин.
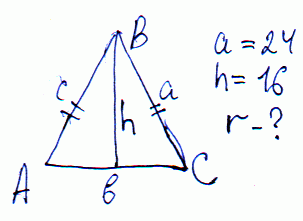
Площадь треугольника по классической формуле равна половине произведения основания на высоту, проведенной к ней. Выполняем вычисления
S=24*16/2=192 (кв. см.)
Для определения периметра нам нужно найти длину боковой стороны.
В равнобедренному треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
По теореме Пифагора находим боковую сторону треугольника
b=sqrt(16^2+(24/2)^2)=20 (см)
Периметр - сумма всех сторон
P=2*20+24=64 (см)
Находим радиус вписанной в треугольник окружности по формуле
r=S/(2*P)=192/(64/2)=192/32=6 (см).
Ответ: 6 (см).
Задача 2 Основание равнобедренного треугольника равно 24 см, боковая сторона 13 см. Вычислите площадь треугольника?
Решение: Площадь равна половине произведения основания на высоту.
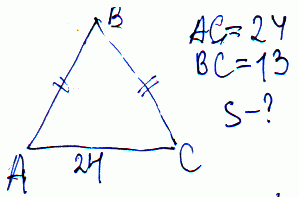
Основание нам известно, высоту находим по теореме Пифагора
h=√(b2-a2/4)= √(169-144)=5 (см).
Далее вычисляем площадь
S=a*h/2=24*5/2=60 (см. кв.)
Ответ: 60 (см. кв.)
Задача 3 Из четырех равных правильных треугольников составили треугольник. Вычислите площадь треугольника DЕF, если периметр треугольника АВС равен 24 см.
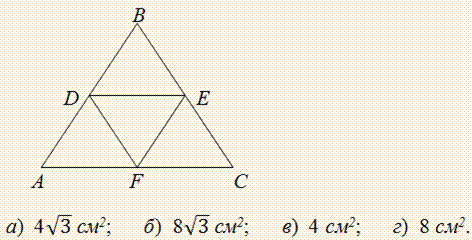
Решение: Под правильным всегда подразумевают равносторонний треугольник.
Разделим заданный периметр на тройку.
a=24/3=8 (см).
Так мы будем иметь сторону большого треугольника. Дальше возможны два пути, или искать сторону малого треугольника и его площадь. Или найти площадь большого треугольника и, по условию, разделить на 4. Рассмотрим второй вариант.
Высота треугольника по Пифагору равна
h=√(8^2-4^2)=4√3 (см).
Найдем площадь треугольника
S=8*4√3/2=16√3 (см. кв.).
Разделив полученное значение на 4 получим искомую площадь треугольника
S1=4√3 (см. кв.)
Такой ответ соответствует первому номеру (А) тестовых вариантов.
Задача 4 Диагональ, боковая сторона и большая основа равнобедренной трапеции равны соответственно 40см, 13 см и 51 см. Найдите радиус окружности, описанной вокруг трапеции.
Решение: Имеем формулу радиуса описанной окружности трапеции по сторонам и диагонали:
R=adc/4√p(p-a)(p-d)(p-c),
где a - боковая сторона, d- диагональ, с - большее основание.
p=(a+d+c)/2=52.
Вычисляем радиус окружности описанной вокруг трапеции
R=26520/(4*√52*39*12*1)=6630/√24336=6630/156= 42,5 см.
Ответ: 42,5 см.
Задача 5 Периметр равнобедренного треугольника 64 см, а боковая сторона на 11 см больше его основания. Найдите высоту треугольника, опущенную на боковую сторону.
а) 13,66 см; б) 13,4 см; в) 13,44 см; г) 15,44 см.
Решение: Составим уравнения по условию.
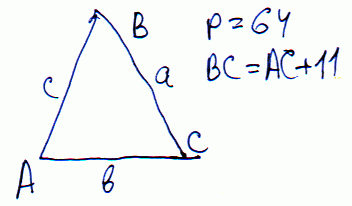
Обозначим основание через Х, тогда боковая сторона – Х+11.
Запишем формулу периметра треугольника
P=2(X+11)+X=3*X+11.
С другой стороны периметр равен 64 см. Получим уравнение
3*Х+22=64 (см);
Х=(64-22)/3=14 (см.)
Боковая сторона равна
X+11=25 см.
Найдем высоту треугольника
h=√ (25^2-(14/2)^2)=24 (см.)
Тогда площадь равнобедренного треугольника равна
S=14*24/2=168 (см. кв.)
Такую же площадь получим, если известна боковая сторона и высота, проведенная к ней
S=h1*25/2=168
Отсюда находим высоту
h1=168*2/25=13,44 (см).
Правильный вариант (в).
Задача 6 Высота равнобедренного треугольника, проведенная к основанию, равна 15 см, а высота, проведенная к боковой стороне – 24 см. Найдите площадь этого треугольника.
а) 270 см2; б) 300 см2; в) 310 см2; г) 285 см2.
Решение:Выполняем схематично построение к задаче.
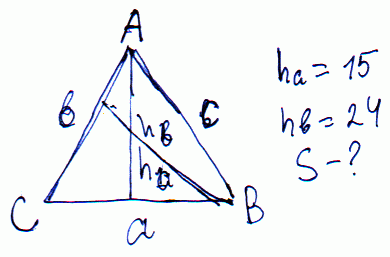
Составим уравнение площади треугольника через известные высоты.
S=a*24/2=b*15/2.
Отсюда имеем отношения для выражения одной стороны через другую
b=24/15*a.
Далее, по теореме Пифагора выразим высоту через боковую сторону и половину основания треугольника
h1=sqrt(a^2-(b/2)^2)=sqrt(a^2-(24*a/15/2)^2)=15 (см.).
Сведя под корнем к общему знаменателю и, выразив неизвестную, получим
a=15*30/18=25 (см.)
Далее находим площадь треугольника
S=24*25/2=300 (см. кв.)
Правильным является вариант (б).
Задача 7 Вычислить площадь равнобедренного треугольника, боковая сторона которого равна 20 см, а высота, проведенная к основанию – 12 см.
а) 192 см2; б) 240 см2; в) 120 см2; г) 96 см2.
Решение:
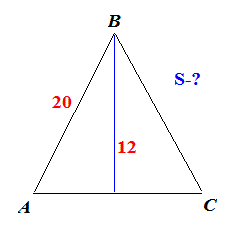
По теореме Пифагора находим основание равнобедренного треугольника
h=sqrt(20^2-12^2)=16 (см).
Находим площадь
S=16*12/2=96 (см. кв.)
Вариант г) является правильным ответом.
Задача 8 Боковая сторона равнобедренного треугольника точкой касания вписанной окружности делится в отношении 12:25, считая от вершины угла при основании треугольника. Найдите радиус вписанной окружности, если площадь треугольника равна 1680 см2.
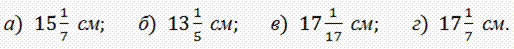
Решение:
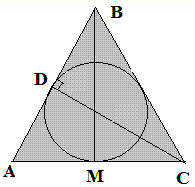
По условию AD/DB=12/25, S=1680.
Обозначим AD=12x, DB=25x.
Из геометрии следует, что AM=12x, а основание треугольника равно 24х.
Из прямоугольного треугольника выразим высоту
h^2=x^2((12+25)^2-12^2).
Далее составим уравнение площади, но для удобства вычислений все умножим на 2 и возведем к квадрату.
(24x)^2*x^2*((12+25)^2-12^2)=(2*1680)^2.
После вычислений получим, что x=2 см.
В соответствии с обозначениями, боковая сторона равна 37*2=74 см , а основание 24*2=48 см.
Радиус вписанной окружности найдем, разделив площадь треугольника на половину периметра.
P=74*2+48=196 см.
P / 2 = 196/2 = 98 см.
r=1680/98=120/7=17 и 1/7.
С тестовых ответов правильный вариант (в).
Задача 9 На медиане ВD равнобедренного треугольника АВС отмечены точки М так, что ВМ:МD=3:1. Найдите площадь треугольника АВС, если площадь треугольника АМD равна 3см2.
а) 27 см2; б) 24 см2; в) 30 см2; г) 25 см2.
Решение: Многие из Вас подумает, что решить задачу невозможно и нужно применять сложные формулы. Но по большому счету имеем пример на логику. Построим схематически треугольник и изобразим известную область.
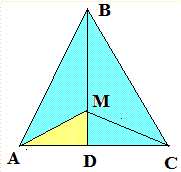
По простой формуле площадь равна половине произведения основания на высоту.
Если рассмотреть треугольники ABD и AMD, то основание в них равно, а высоты относятся как (3+1):1.
Таким образом площадь треугольника ABD в 4 раза больше, чем AMD, а целого равнобедренного треугольника в два раза больше найденного прямоугольного ABD.
Таким образом, площадь SABC=2*4*SAMD=8*3=24 см. кв., что соответствует варианту (б) тестов. Вот такие простые рассуждения позволяют решить непростую на первый взгляд головоломку.
Задача 10 Периметр равнобедренного треугольника равен 100 см, а высота, опущенная к основанию – 30 см. Найдите площадь треугольника.
а) 480 см2; б) 420 см2; в) 560 см2; г) 460 см2.
Решение: Задан пример на составление уравнений.
Обозначим основание треугольника через а, а боковую сторону – b.
Уравнение периметра дает зависимость
P=2*b+a=100.
Запишем формулу квадрата высоты треугольника
b^2-(a/2)^2=30^2.
Из периметра выразим половину основы и подставим во второе уравнение
b^2-(50-b)^2=30^2.
После упрощений получим 100*b=50^2+30^2, отсюда
b=34 см.
а=50 - b=16 см.
Имеем основание и высоту, можем определить площадь треугольника по формуле
S=16*30/2=240 (см. кв.)
На удивление такой ответ отсутствует среди возможных вариантов.
Задача 11 В равнобедренном треугольнике боковая сторона равна 10см, а высота, проведенная к основанию – 6 см. Найти площадь треугольника.
а) 96 см2; б) 60 см2; в) 48 см2; г) 36 см2.
Решение: Выполняем вспомогательный рисунок к примеру.
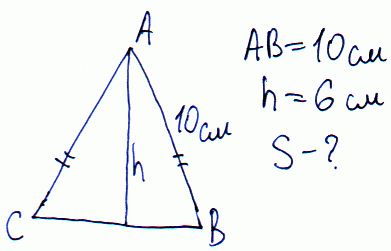
Задания на применение теоремы Пифагора.
Вычисляем половину основания треугольника
a/2=sqrt(10^2-6^2)=8 см. а=2*8=16 см.
После – площадь треугольника
S=16*6/2=48 (см. кв.)
Верным ответом на тестах является вариант (в).
Задача 12 В равнобедренном треугольнике высота, проведенная к боковой стороне, делит ее на отрезки 8 см и 2 см, начиная от вершины угла между боковыми сторонами. Найдите площадь треугольника.
Решение:
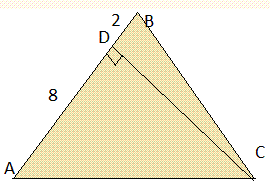
Из рисунка можем подсмотреть сам ход вычислений. Сначала найдем высоту, а дальше площадь.
Гипотенуза треугольника DBC равна
2+8=10 см.
Вычисляем высоту
10^2-2^2=h^2;
h^2=96;
h=4*sqrt(6).
Далее находим площадь
S=1/2*10*4√6=20√6 см2.
Задача 13 Периметр равнобедренного треугольника равен 128 см, а боковая сторона относится к основанию, как 5:6. Вычислить диаметр вписанного круга.
Решение: Обозначим основание через 6*a, боковую соответственно – 5*a.
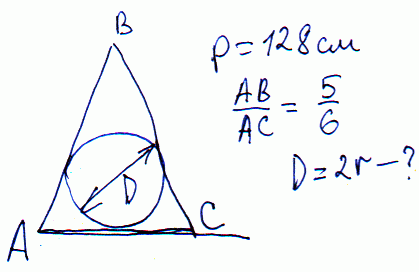
Составляем уравнение периметра
P=2*5*a+6*a=16*a.
Отсюда a=128/16=8 см.
Согласно обозначенным параметрам, основа равна 6*a=48 см,
стороны треугольника 5*8=40 см.
Найдем высоту по известной формуле Пифагора
h=sqrt(40^2-24^2)=32 см.
Вычисляем площадь S=48*32/2-на карте=768 см. кв.
Радиус вписанного в треугольник круга равен отношению площади к половине периметра
R=768/(128/2)=12 см.
Ответ: R=12 см.
Задача 14 Периметр равнобедренного треугольника равен 160 см, а высота, опущенная к основанию равна 40см. Найти все стороны треугольника.
Решение:
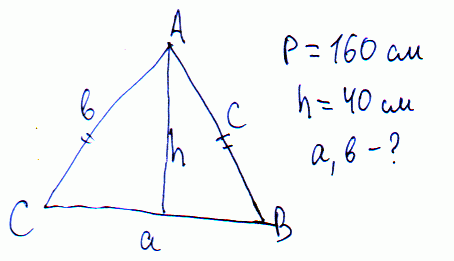
Составляем два уравнения: высоты через теорему Пифагора и периметра.
a+2*b=160;
b^2-(a/2)^2=40^2.
Из первого выражаем a/2 и подставляем во второе
b^2-(80-b)^2=40^2.
Отсюда
160*b=40^2+80^2;
b=50 см.
a=160-2*50=60 см.
Стороны треугольника равны 50, 50, 60 см.
Задача 15 Боковая сторона равнобедренного треугольника равна 55 см, а его основание равно 66см. Вычислить длину отрезков, на которые делит боковую сторону биссектриса угла при основании.
Решение: Обозначим через x, y – отрезки, на которые биссектриса делит боковую сторону.
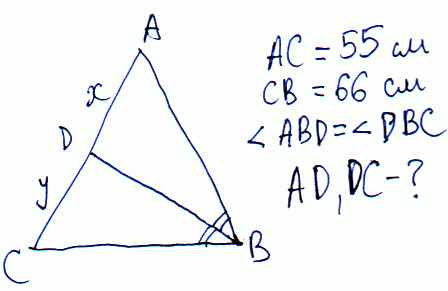
По теореме о пропорциональных отрезках имеем
55/x=66/y, x=55/66*y.
Второе соотношение дает условие, что сумма отрезков равна боковой стороне
x+y=55.
При подстановке первого уравнения во второе получим
(55/66+1)*y=55.
Отсюда y=30 см, x=55-30=25 см.
На этом все вычисления к заданию, рассматрите повнимательней етот ответ.
Задача 16 Боковая сторона и основание равнобедренного треугольника относятся, как 5:6, а периметр его равен 48 см. Найти расстояние от точки пересечения медиан до основания.
Решение: Обозначим стороны треугольника через 5x, 6x соответственно.
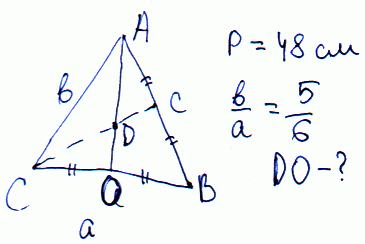
Тогда уравнение периметра запишем в виде
2*5*x+6*x=48;
16*x=48;
х=48/16=3 см.
Отсюда вычисляем основание равнобедренного треугольника
6*x=18 см
и боковые стороны – 5*x=15 см.
Задача 17 Биссектриса, проведенная к боковой стороне равнобедренного треугольника, делит ее на отрезки 25 см и 30 см , начиная от вершины, которая противоположна основе. Вычислить периметр треугольника.
Решение: Обозначим основание и боковую стороны через a, b соответственно.
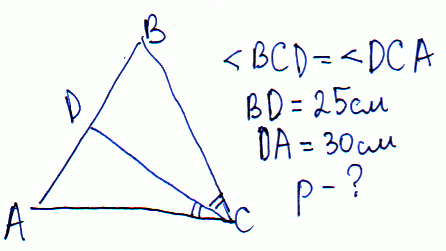
По свойству треугольника составляем зависимость a/30=b/25.
С другой стороны, боковую сторону можем определить
b=25+30=55 см.
Выразим основу с первой зависимости
a=30*b/25=30*55/25=66 см.
находим периметр равнобедренного треугольника
P=66+2*55=176 см.
Задача 18 Боковая сторона равнобедренного треугольника равна 25 см, а высота, опущенная к ней - 24 см. Найти периметр треугольника.
Решение Еще один не простой на первый взгляд пример. Выполняем решения с построение рисунка.

Площадь равна половине произведения основания на высоту. С одной стороны это
S=1/2*25*24=300 см. кв.
С другой стороны обозначим основу через 2x, по теореме Пифагора найдем высоту, а потом и площадь
h=sqrt (25^2x^2);
S=1/2*2*x*sqrt(25^2-x^2).
Приравняв площади, получим уравнение для отыскания основания
x*sqrt (25^2-x^2)=300.
возведем зависимость к квадрату и сгруппируем, в результате получим биквадратное уравнения
x^4-225*x^2+90000=0.
Выполнив замену y=x^2 , сведем его к виду
y^2-225*y+90000=0.
Корни квадратного уравнения равны
y1=400, y2=225.
Отсюда x1=20, x2=15.
Основание треугольника равно 2*x, поэтому в первом случае оно равна 40 см, во втором 30 см . Многим из Вас непонятно, как такое может быть. Дело в том, что при основании 40 высота будет проектироваться не в боковую сторону, а на ее продолжение. Поэтому такой вариант хоть и правильный геометрически, но мы его исключаем. Окончательно периметр равен
P=2*25+30=80 см.
Задача 19 В равнобедренном треугольнике высота, опущенная на основание, равна 32 см. Биссектриса угла при основании пересекает данную высоту в точке, которая удалена от основания на 12 см. Найти основание треугольника.
Решение: Кое-что подправим предварительный рисунок к новому заданию. В «Paint» это делать довольно легко.
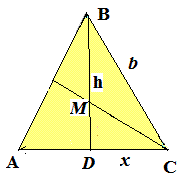
Имеем MD=12, высота h=32 тогда BM=32-12=20 см.
По свойству биссектрисы - она делит высоту на пропорциональные сторонам отрезки, то есть
b/20=x/12.
Второе уравнение получим из теоремы Пифагора
b^2-x^2=h^2=32^2.
Выражаем из первой зависимости одну из неизвестных и подставляем во второе
x=12/20*b;
b^2-(12/20*b)^2= 32^2.
Решение уравнения b=40 см.
Находим вторую неизвестную - x=12/20*40=24 см.
Так, как основание треугольника в два раза больше x, то оно равно 48 см.
Постарайтесь заучить или сгруппировать в памяти подобные схемки вычислений, на контрольной и тестах это помогает в выборе правильного (быстрого) метода расчетов.
Задача 20 В равнобедренному треугольнике угол, образованный высотой, проведенной к основанию, и биссектрисой угла при основании равен 55 градусов. Найти все углы треугольника.
Решение: Выполним вспомогательный рисунок.
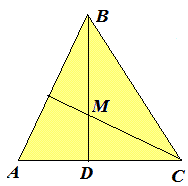
Угол DMC равный 55 градусов. Угол DCM равный 180-90-55=35 градусов.
Поскольку имеем биссектрису, то угол MCB=DCM=35.
Угол при основании равен 2*35=70 градусов.
При вершине равнобедренного треугольника угол равный
180-2*70=40 градусов.
На этом все угловые меры найдено.
Задача 21 В равнобедренному треугольнике основание равно 10 см, а высота – 20 см. Найти высоту опущенную на боковую сторону.
Решение:
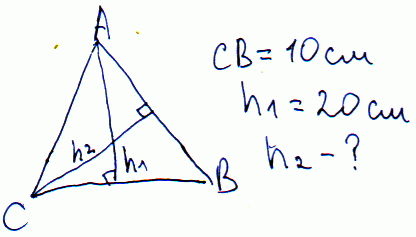
Найдем неизвестную высоту через уравнение площади
S=1/2*20*10=100 см. кв.
Вычислим боковую сторону
b=sqrt(20^2-(10/2)^2)=5√15
и площадь
S=1/2*b*h=100;
Отсюда находим вторую высоту
h2=2*100/b=8/3*√15 см.
Задача 22 Основание равнобедренного треугольника равно 30 см, а высота опущенная на боковую сторону – 24 см. Вычислить периметр треугольника.
Решение: Обозначим отрезки на которые делит боковую сторону высота через a,x, начиная с основы.
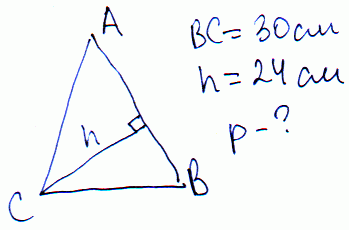
По теореме Пифагора составляем 2 уравнения:
a^2=30^2-24^2;
(a+x)^2-x^2=24^2.
При вычислении системы уравнений получим значение
x=7, a=18.
Отсюда боковая сторона равнобедренного треугольника равна 18+7=25 см, а его периметр
P=30+2*25=80 см.
Задача 23 На медиане равнобедренного треугольника, проведенной к основанию, взята точка, одинаково удаленная от концов боковой стороны. Вычислить периметр треугольника если расстояние от этой точки до основания равно 14 см, а к концу основания – 50 см.
Решение: Без дополнительного построения здесь не разобраться.
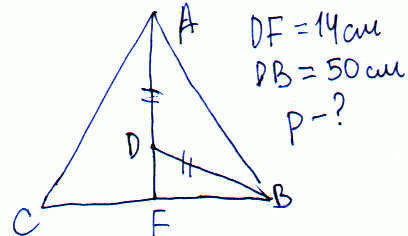
Из рисунка видим, что половину основы можем найти из прямоугольного треугольника
a^2=50^2-14^2
отсюда a=48 см, а основание равно 2*48=96 см.
Также по условию, часть высоты после точки равна 50 см, а вся высота 50+14=64 см.
Из прямоугольного треугольника выражаем боковую сторону
c^2=64^2-48
отсюда c=80 см.
Находим периметр
P=80*2+96=256 см.
Везде где Вам непонятно условие, или что от Вас требуют - используйте вспомогательные рисунки. В большинстве задач это позволяет увидеть ход дальнейших вычислений.
Задача 24 Медиана равнобедренного треугольника, проведенная к основанию, делит высоту, опущенную на боковую сторону на отрезки 75 и 21см, начиная от конца основания. Найдите стороны треугольника.
Решение: Сначала выполняем вспомогательный рисунок

По свойству равнобедренного треугольника медиана проведенная к основанию одновременно является и высотой и биссектрисой. Поэтому с одной стороны можем составить зависимость
x/21=b/75.
С другой стороны, треугольник CDB прямоугольный, поэтому по теореме Пифагора имеем
x^2+(21+75)^2=b^2.
Выразим из первого уравнения x и подставим во второе
x=21/75*b;
96^2=b^2*(21/75* b)^2.
В результате вычислений получим b=100.
Тогда одна из частиц, которую отсекает высота от боковой стороны равна
X=21*100/75=28 см.
Остальная AD равна
AD=100-28=72 см.
Основу равнобедренного треугольника находим как гипотенузу
ADC: 72^2+96^2=a^2.
Отсюда a=120 см.
Стороны равны 120 см и две по 72 см.
Больше готовых ответов по геометрии Вы можете найти в соседних публикациях.
До встречи и хорошего Вам обучения!
Пример 31.29 В равнобедренному треугольнике центр вписанного круга делит высоту, проведенную к основанию, в отношении 12:5, а боковая сторона равна 60. Найти периметр треугольника.
Решение: Пусть имеем равнобедренный треугольник ABC, у которого AC=BC=60 - боковые стороны.
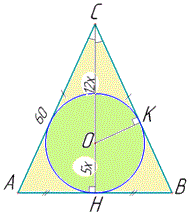
В ΔABC вписано окружность с центром в точке O, причем CO:HO=12:5 (по условию). Проведем радиус вписанной окружности OK к стороне BC, тогда OK⊥BC (по свойству). Пусть HO=5x - радиус вписанной окружности, тогда OK=HO=5x и CO=12x.
Рассмотрим прямоугольные треугольники ΔAHC (∠H=90) и ΔOKC (∠K=90). У них острые углы при вершине C одинаковые (ведь HC - высота, медиана и биссектриса).
Отсюда следует, что треугольники ΔAHC и ΔOKC подобные, а поэтому их соответствующие стороны пропорциональны:
AC/CO=AH/ОК
отсюда
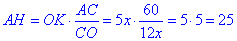
Поскольку HC - медиана, то AB=2•AH=2•25=50.
Найдем периметр равнобедренного треугольника ΔABC
PΔABC =2•AC+AB=2•60+50=170.
Ответ: 170.
Пример 31.30 Периметр равнобедренного треугольника равен 108 см, а основание - 30 см. Найти (в см) площадь треугольника и радиус вписанной окружности.
Решение: Пусть задан равнобедренный треугольник ABC, у которого AC=BC - боковые стороны, AB=30 см - основа и PΔABC=108 см - периметр (по условию).
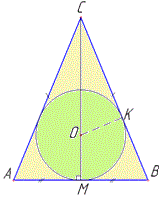
Найдем боковую сторону ΔABC :
PΔABC=2•AC+AB=108, отсюда
AC=BC=(PΔABC-AB):2=(108-30):2=39 (см).
Проведем высоту CM к основанию AB равнобедренного ΔABC (CM⊥AB), тогда по свойству, CM - медиана и биссектриса, то есть AM=BM=AB2=30/2=15 (см).
В прямоугольном ΔAMC (∠M=90) по теореме Пифагора найдем катет CM - высоту ΔABC AM^2+CM^2=AC^2, отсюда
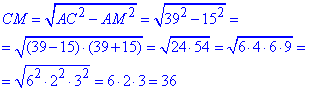
Вычислим площадь равнобедренного треугольника ΔABC по классической формуле:
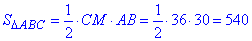 (см2).
(см2).
Найдем полупериметр ΔABC:
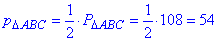 (см).
(см).
Определим радиус вписанной окружности в ΔABC по формуле:
r=S/p=540/54=10(см).
Ответ:540; 10.
Пример 31.31 Основание равнобедренного треугольника равно 12, а высота, проведенная к основанию - 8. Найти площадь треугольника и радиус окружности, вписанной в этот треугольник.
Решение Имеем равнобедренный треугольник ABC, у которого AC=BC - боковые стороны, AB=12 - основание и CM=8 - высота, проведенная к основанию AB, CM⊥AB (по условию). Тогда по свойству, CM - медиана и биссектриса, то есть
AM=BM=AB/2=12/2=6 .
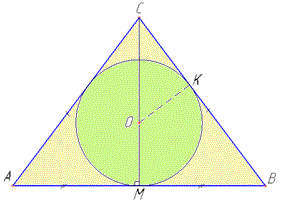
В прямоугольном ΔAMC (∠M=90) по теореме Пифагора найдем гипотенузу AC - боковую сторону ΔABC:
AC^2=AM^2+CM^2, отсюда
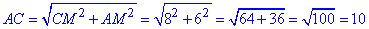
Найдем площадь ΔABC по формуле:
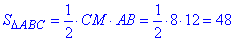
Полупериметр треугольника ΔABC:
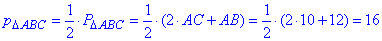
Вычислим радиус вписанной окружности в треугольнике ABC по формуле:
r=S/p=48/16=3 .
Ответ: S=48, r=3.
Пример 31.35 Найти площадь равнобедренного треугольника с точностью до 0,01 см2, если высота, проведенная к боковой стороне, равна 12 см, а другая высота - 9 см.
Решение Пусть имеем равнобедренный треугольник ABC, у которого AC=BC - боковые стороны, AB - основа и CM=9 см - высота, проведенная к основанию AB, CM⊥AB, AK=12 см - высота, проведенная к боковой стороне BC, AK⊥BC (по условию).
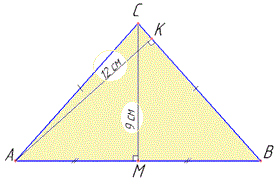
По свойству высоты проведенной к основанию равнобедренного ΔABC имеем:
AB=2BM.
Запишем формулы для вычисления площади ΔABC:
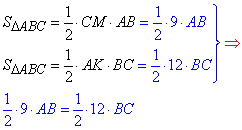
Отсюда BC=0,75*AB=0,75*2*BM=1,5BM, следовательно BC=1,5•BM .
В прямоугольном треугольнике ΔBMC(∠M=90) по теореме Пифагора найдем катет BM:
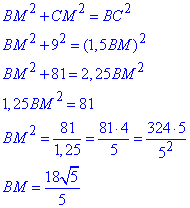
Тогда AB=2•BM=36√5/5 (см).
Найдем площадь равнобедренного ΔABC с точностью до 0,01:
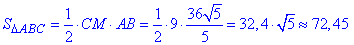
Ответ: 72,45.
Задача 1 Центр окружности, вписанной в треугольник, делит высоту проведенную к основанию на отрезки 13 и 5 см. Найти периметр треугольника.
Решение Поскольку центр круга (точка O), вписанного в треугольник ABC, лежит на высоте BM, то ΔABC - равнобедренный.
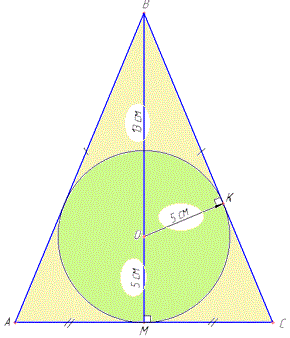
AB=BC - боковые стороны, AC - основа равнобедренного треугольника ΔABC, BM - высота равнобедренного треугольника ABC, проведенная к основанию AC (BM⊥AC). По свойству AM=CM, отсюда AC=2CM.
По условию задания BM=BO+OM=13+5=18 см. OM=OK=5 см - радиус вписанной окружности. По свойству вписанной в треугольник окружности OK⊥BC.
Рассмотрим прямоугольный треугольник OBK, у которого ∠BOK=90, OK=5 см - катет, OB=13 см - гипотенуза. По теореме Пифагора найдем катет BK:
OB^2=BK^2+OK^2, отсюда
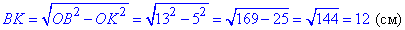
Рассмотрим прямоугольные треугольники OBK (∠BOK=90) и CBM (∠BMC=90).
В них ∠OBK=∠MBC (то есть острый угол при вершине B общий, а потому ровный). Отсюда следует, что прямоугольные ΔOBK и ΔBCM - подобные треугольники.
По свойству подобия треугольников (стороны подобных треугольников пропорциональны) имеем BK/BM=OK/CM, отсюда 12/18=5/CM, CM=5•18/12=7,5 см.
По свойству окружности, вписанной в треугольник, имеем KC=CM=7,5 см.
Вычислим длины сторон равнобедренного ΔABC:
AC=2CM=2•7,5=15 см;
AB=BC=BK+KC=12+7,5=19,5 см.
Вычислим периметр треугольника ΔABC:
PΔABC=AB+BC+AC=19,5+19,5+15=54 см.
Ответ: 54 см.
На сайте опубликовано около 1000 задач на различные геометрические фигуры. Помощь понятны как для школьника в 10-11 классе, так и для студента. Если есть желание, можете дополнить любую статью качественными задачами.
Все в Ваших руках, берите и учитесь!
Напомним что параллелограммы при сторонам имеют как острые так и тупые углы (смотрите рисунок ).
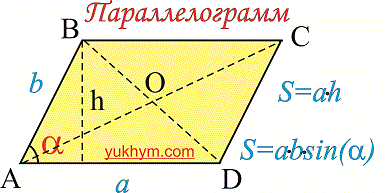
Прямоугольником называют такой параллелограмм у которого все углы прямые. Все это обобщенно, поскольку, если параллелограмм имеет хотя бы один прямой угол то все остальное - также прямые. Большинство предметов которые нас окружают имеют форму прямоугольника: стол, окна, двери, комнаты, участки земли и т.п.
Рассмотрим прямоугольник
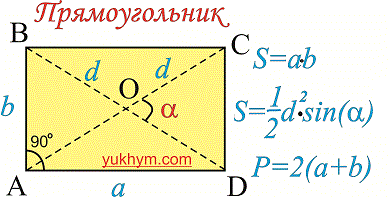
Точки А, В, С и D принято называть вершинами прямоугольника, а отрезки, которые соединяют АВ, ВС, CD и AD - сторонами прямоугольника (ширина и длина). Те из сторон которые имеют общую вершину называются соседними. Остальные не подпадающие этому определению называют противоположными ( Противоположные стороны параллельны между собой).
Отрезок соединяющий наиболее отдаленные вершины называется диагональю прямоугольника.
Свойства прямоугольника
Рассмотрим чем отличается прямоугольник от других фигур.
1. В прямоугольнике противоположные стороны равны.
2. Уровни между собой и имеют 90 градусов все углы прямоугольника.
3. Диагонали прямоугольника равны и в точке пересечения делятся пополам.
4. Диагонали треугольника делят его на два одинаковых треугольника.
Таким образом, если в параллелограмме все углы ровны или один прямой, или одинаковые диагонали то это прямоугольник. Что касается четырехугольников, то среди них прямоугольниками будут только те, у которых все углы равны или хотя бы три прямые. Биссектриса угла прямоугольника отсекает от него равнобедренный треугольник.
Основными геометрическими характеристиками прямоугольника является периметр и площадь.
Периметр прямоугольника - формула
Периметр равен сумме всех сторон, при этом стороны попарно равны между собой. Поэтому формула периметру прямоугольника имеет вид
P=2(a+b).
Пример 1. Стороны прямоугольника равны 5 и 7 см. Найти его периметр.
Решение. Подставляем значения в формулу периметру прямоугольника
P=2(5+7)=24 (см).
Ответ. Периметр равен 24 см.
Формула площади прямоугольника
Площадь прямоугольника равна произведению его ширины на высоту.
S=a*b.
Если задано длину диагоналей (d) и угол между ними (alpha) то формула площади прямоугольника равна половине квадрата диагоналей на синус угла между ними.
S=d*d*sin(alpha)/2.
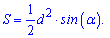
Не забывайте что площадь измеряется в единицах квадратных, поэтому если размеры заданы в метрах то площадь будет в метрах квадратных, сантиметрах - площадь в сантиметрах квадратных и т.п.
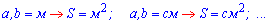
Пример 2. Диагонали прямоугольника пересекаются под углом 30 градусов и ровны 5 см. Какова площадь прямоугольника?
Решение. Подставляем данные в формулу площади прямоугольника через диагонали
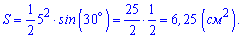
Ответ. Площадь равна 6,25 сантиметров квадратных.
Диагонали прямоугольника
В прямоугольнике длину диагонали вычисляют через длины сторон по теореме Пифагора
d=sqrt(a^2+b^2) или 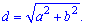
Итак Вы уже знаете как найти площадь прямоугольника, периметр и диагональ.
Стороны прямоугольника
Если известна диагональ и одна сторона то вторую также определяем по теореме Пифагора
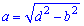 или
или 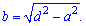
Описанная и вписанная окружность в прямоугольник
Диаметр или радиус описанной вокруг прямоугольника окружности Вы видимо вычисляли. Однако вряд ли задумывались о вписанной окружности и геометрическом место ее центров.
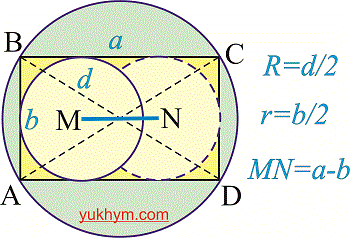
Диаметр описанной окружности равен диагонали (d), соответственно радиус описанной окружности - половине диагонали (R=d/2). Вписанных окружностей в прямоугольник можно построить множество. Радиус вписанной окружности равен половине длины меньшей стороны прямоугольника (r=b/2). Если соединить центры всех возможных вписанных окружностей то получим отрезок MN длина которого равна разности сторон (MN=a-b).
Приведенная информация о вписанной и описанной окружности редко пригодится Вам при решении задач но Вы должны знать как в таких случаях вычислять указанные величины.
Задачи на прямоугольник
Стороны прямоугольника
Задача 1. Длина диагонали и стороны прямоугольника составляют 10 и 8 см. Найдите другую сторону.
Решение. По теореме Пифагора вычисляем
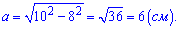
Ответ. Сторона равна 6 см.
-------------------------------
Задача 2. Длина диагонали прямоугольника равна 5 см. Одна сторона меньше другой на сантиметр. Найдите стороны прямоугольника.
Решение. Обозначим первую сторону через х, тогда по условию вторая – х -1. Составляем уравнение
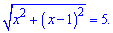
Возводим к квадрату и решаем квадратное уравнение
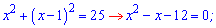
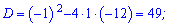
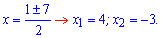
Второе значение не имеет смысла. Для вычисления меньшей стороны выполняем вычитание
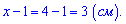
Ответ. Стороны прямоугольника равны 3 и 4 см.
-------------------------------
Задачи на площадь и периметр прямоугольника
Задача 3. Большая сторона прямоугольника 8 см. Меньшая составляет четверть большой. Какая площадь и периметр прямоугольника?
Решение. Четверть большей означает одна четвертая часть, то есть
b= 8/4=2 (см).
Площадь и периметр находим по формулам
P=2(2+8)=20 (см); S=2*8=16 (см^2).
Ответ. Периметр 20 см, площадь 16 сантиметров квадратных.
-------------------------------
Задача 4. Участок земли имеет площадь 64 квадратных метров. Какой периметр участка если диагонали пересекаются под прямым углом?
Решение.
Поскольку угол между диагоналями 90 градусов, то это квадрат. Площадь квадрата равна квадрату стороны
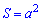
Отсюда находим сторону
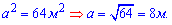
Периметр находим по формуле
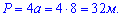
Ответ. Периметр равен 32 метра.
Не забывайте что периметр измеряется в единицах длины, а площадь - в единицах квадратных.
Теперь Вы знаете как найти периметр и площадь прямоугольника. Пользуйтесь формулами на практике и совершенствуйте навыки вычислений указанных величин.
Посмотреть материалы:
]]>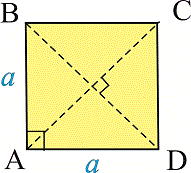
Квадрат наиболее симметричная фигура среди всех четырехугольников.
Свойства квадрата
Свойства квадрата - это основные признаки которые позволяют распознать его среди прямоугольников, ромбов, четырехугольников:
- В квадрата все стороны и углы равны AB=BC=CD=AD.
- Противоположные стороны параллельны между собой
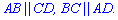
- Углы между соседними сторонами прямые.
- Диалонали квадрата равны и пересекаются под прямым углом.
- Диагонали является одновременно биссектрисами углов квадрата.
- Точка в которой пересекаются диагонали является центром квадрата, кроме этого - центром вписанной и описанной окружности.
- Диагонали делят квадрат на четыре одинаковые равнобедренные прямоугольные треугольники .
Площадь квадрата
Больше примеров в школьном курсе при изучении квадрату связано с вычислением его площади и периметра. Вам может показаться что для вычисления площади достаточно знать одну формулу S=a*a и этого хватит для всех задач, однак это не так. Поскольку быстро информация воспринимается и изучается визуально, то мы объединили все величины квадрата которые Вам придется вычислять и нарисовали простые и понятные рисунки с формулами. Их без трудностей можете скачать по ссилке внизу статьи.
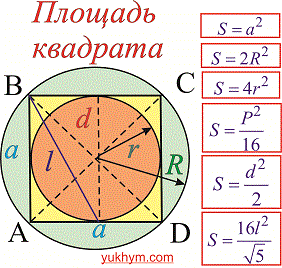
Большинство обозначений Вам понятна, но повторим их снова
a– сторона квадрата;
d– диагональ;
P– периметр;
S– площадь;
R– радиус описанной окружности;
r– радиус вписанной окружности;
l– отрезок изображен на рисунке (часто используется в сложных примерах).
Формулы площади квадрата которые приведены ниже дают возможность вычислять ее через периметр, сторону, диагонали, радиусы .
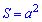
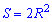
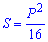
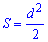
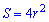
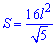
Они не слишком сложные и каждая из них может Вам пригодиться для вычисления площади квадрата.
Периметр квадрата
Что может быть проще вычисления периметра квадрата если конечно известно его стороны. Однако, если задана только диагональ, площадь, радиус то нахождение периметра не так очевидно. Приведенный ниже рисунок содержит самые необходимые формулы для вычисления параметра
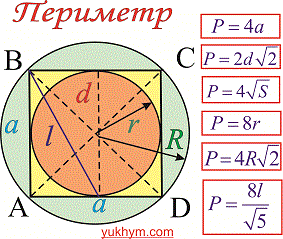
Сами же формулы периметру от различных параметров квадрату привидены ниже
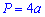
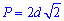
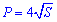
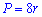
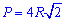
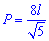
Диагональ квадрата
Диагональ квадрата может бить выражена через радиусы вписанной, описанной окружностей, сторону, периметр, площадь следующими формулам.
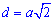
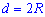
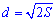

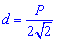
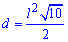
В качестве справочника формул диагонали квадрата можете использовать следующий рисунок.
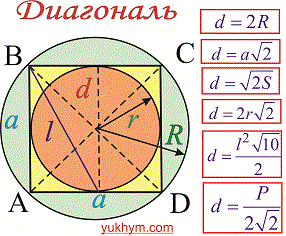
Радиус описанной окружности
Простейшая для вычислений формула радиуса описанной окружности R=d/2, т.е. радиус равен половине диагонали квадрата. Все последующие формулы которые помогут определить радиус описанной окружности содержат корни, однако при вычислениях незаменимы.
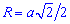
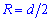
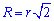
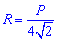
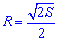
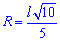
Ниже изображен вспомогательный рисунок с приведенным всеми формулами.
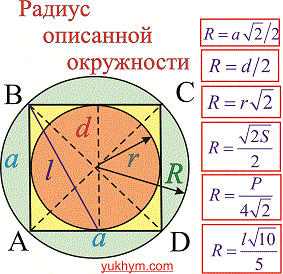
Радиус вписанной окружности в квадрат
Радиус вписанной окружности из рисунка равный половине его стороны.
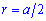
Также он равной одной восьмой части периметра. Зависимости для нахождения радиуса вписанной окружности через площадь, диагональ, радиус описанной окружности содержат иррациональности. Однако и в условиях примеров величины, известные для вычисления радиуса, как правило, заданны с корнями или такими которые легко упрощаются (например 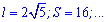 ).
).
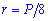
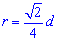
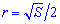
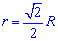
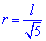
Черновик-подсказка формул радиуса вписанной в квадрат окружности приведена ниже
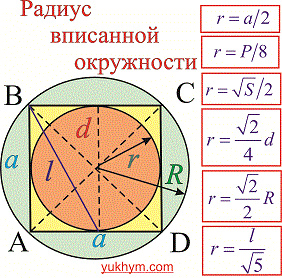
Если же задано диаметр вписанной или описанной окружности то делим пополам (чтобы получить радиус) и можем применять в приведенных формулах. Это Вы думаю помните.
Бонус для всех школьников и студентов. Все цветные графики с формулами площади квадрата, его периметра, диагонали, радиусов вписанной и описанной окружности Вы можете скачать по ссылке внизу.
Распечатывайте формулы и пользуйтесь в обучении.
{jd_file file==18}
Понравился материал - поделись ссылкой с друзьями.
Посмотреть материалы:
- Прямоугольный треугольник. Задачи
- Площадь треугольника. Формулы
- Периметр и площадь прямоугольника
- Периметр и площадь параллелограмма
- Формулы площади трапеции
- Ромб. Площадь, периметр
{jcomments on}
]]>Приведенные ниже формулы позволят решить 95 процентов задач в которых требуется найти площадь треугольника.
Перейдем к рассмотрению распространенных формул площади.
Рассмотрим треугольник изображен на рисунке ниже

На рисунке и далее в формулах введены классические обозначения всех его характеристик
a,b,c – стороны треугольника,
R– радиус описанной окружности,
r – радиус вписанной окружности,
h[b],h[a],h[c] – высоты , проведенные в соответствии со сторонами a,b,c.
alpha, beta,hamma – углы возле вершин.
Основные формулы площади треугольника
1. Площадь равна половине произведения стороны треугольника на высоту опущенной к этой стороне. На языке формул это определение можно записать так
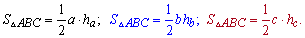
Таким образом, если известна сторона и высота - то площадь найдет каждый школьник.
Кстати, из этой формулы можно вывести одну полезную зависимость между высотами
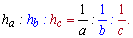
2. Если учесть, что высота треугольника через соседнюю сторону выражается зависимостью
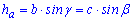
то с первой формулы площади следуют однотипные вторые
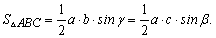
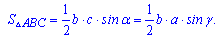
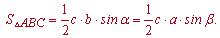
Внимательно посмотрите на формулы - их легко запомнить, поскольку в произведении фигурирует две стороны и угол между ними. Если правильно обозначить стороны и углы треугольника (как на рисунке выше) то получим две стороны a,b и угол связан с третьей С (hamma).
3. Для углов треугольника справедливо соотношение
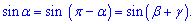
Зависимость позволяет применять в вычислениях следующие формулы площади треугольника
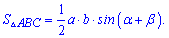
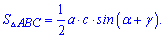
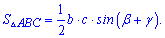
Примеры на эту зависимость встречаются крайне редко, но помнить что есть такая формула Вы должны.
4. Если известна сторона и два прилегающих угла то площадь находится по формуле
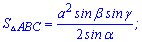
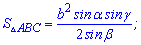
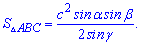
5. Формула площади через сторону и котангенс прилегающих углов следующая
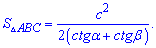
Перестановкой индексов можете получить зависимости для других сторон.
6. Приведенная ниже формула площади используется в задачах когда вершины треугольника заданы на плоскости координатами 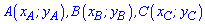 . В этом случае площадь равна половине определителя взятого по модулю.
. В этом случае площадь равна половине определителя взятого по модулю.
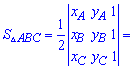
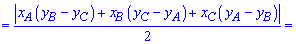
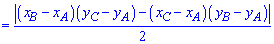
7. Формула Герона применяют в примерах с известными сторонами треугольника.
Сначала находят полупериметр треугольника
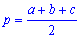
а затем определяют площадь по формуле
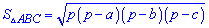
или
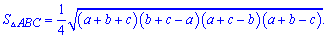
Ее довольно часто используют в коде программ калькуляторов.
8. Если известны все высоты треугольника то площадь определяют по формуле
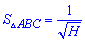
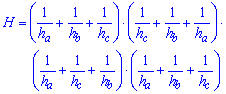
Она сложна для вычисления на калькуляторе, однако в пакетах MathCad, Mathematica, Maple площадь находится на «раз два ».
9. Следующие формулы используют известны радиусы вписанных и описанных окружностей.
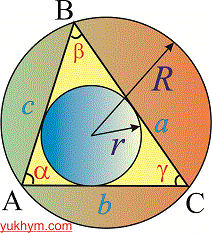
В частности, если известно радиус и стороны треугольника, или его периметр то площадь вычисляется согласно формуле
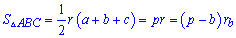
10. В примерах где задано стороны и радиус или диаметр описанной окружности площадь находят по формуле
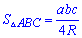
11. Следующая формула определяет площадь треугольника через сторону и углы треугольника.
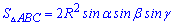
Ну и напоследок - частные случаи :
Площадь прямоугольного треугольника с катетами a и b равна половине их произведения
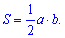
Формула площади равностороннего ( правильного ) треугольника=
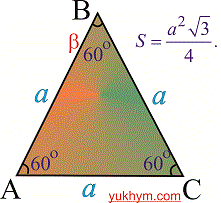
= одной четвертой произведения квадрату стороны на корень из тройки.
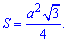
Пример. Стороны треугольника равны 3, 5, 6 см. Найти площадь треугольника.
Решение: Применим формулу Герона, для этого сначала найдем полупериметр
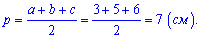
Подставляем в формулу площади
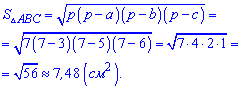
Ответ:Площадь треугольника равна 7.48 сантиметров квадратных.
------------------------------------
Скачать все приведенные формулы площади треугольника Вы можете по следующей ссылке. Распечатывайте их и используйте в обучении.
{jd_file file==19}
Если материал был полезен Вам - поделитесь ссылкой с друзьями.
Посмотреть материалы:
- Прямоугольный треугольник. Задачи
- Периметр и площадь прямоугольника
- Квадрат. Формулы
- Периметр и площадь параллелограмма
- Формулы площади трапеции
- Ромб. Площадь, периметр
{jcomments on}
]]>Задача 1. Найдите синусы острых углов и гипотенузу прямоугольного треугольника если его катеты равны: а ) 6 см и 8 см; б) 4 см и 7 см.
Решение. Применим теорему Пифагора к заданным катетам
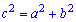
Для задания а) гипотенуза равна

та для б) соответственно
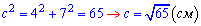
Синус острого угла в прямоугольном треугольнике равен отношению катета напротив угла к гипотенузе.
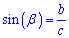
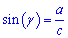 .
.
Рисунок с необходимыми формулами для синусов и формулой Пифагора приведен ниже
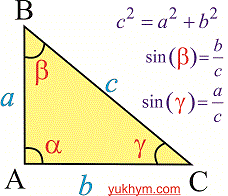
Вычисляем синусы искомых углов
а) 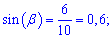
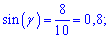
б)
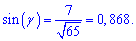
На этом пример завершен.
------------------------
Задача 2. Найдите катеты прямоугольного треугольника если его гипотенуза и второй катет соответственно равны: а ) 15 см и 9 см; б) 8 см и 4 см.
Решение. На основе теоремы Пифагора получим
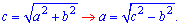
Подставляем значения
а) 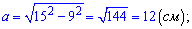
б) 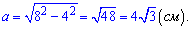
Ответ: Катеты треугольника равны 12 см и  см.
см.
------------------------
Задача 3. В прямоугольном треугольнике гипотенуза равна 17 см. Один из катетов на 7 см меньше гипотенузы. Определиите катеты треугольника.
Решение. Для заданного примера и подобных ему необходимо составлять уравнения. В этом примере обозначим через
x – большой катет. Тогда x-7 – меньший катет.
По формуле Пифагора имеем
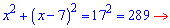
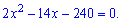
Делим на два и решаем квадратное уравнение с помощью дискриминанта
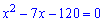
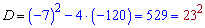
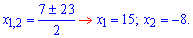
Второй корень уравнения исключаем, поскольку он противоречит условию задачи. Таким образом один катет равен 15 см, а второй – 15-7=8 см.
Ответ: Катеты прямоугольного треугольника равны 15 и 8 см.
------------------------
Задача 4. Вычислите длину высоты равностороннего треугольника сторона которого равна 12 см.
Решение. Если треугольник равносторонний то высота делит основание пополам. Кроме этого высота является перпендикуляром. Таким образом задача состоит в нахождении катета когда известно, что гипотенуза равна 12 см, а второй катет – 12/2=6 см.
По теореме Пифагора вычисляем
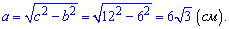
Ответ: Катет равен  см.
см.
------------------------
Задача 5. Сторона квадрата равна 7 см. Определите длину диагонали.
Решение. Поскольку стороны квадрата равны то нужно найти гипотенузу прямоугольного равнобедренного
треугольника с катетами длиной 7 см. Используем известную формулу Пифагора
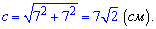
Ответ: Диагональ квадрата равна 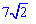 см.
см.
------------------------
Задача 6. Большая диагональ и большая основа прямоугольной трапеции равны соответственно 8 см и 6 см. Найдите длину меньшей боковой стороны трапеции.
Решение. Рассмотрим вспомогательный рисунок трапеции.
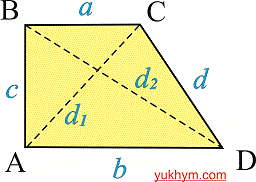
По условию известна диагональ BD=8 см и AD=6 см. Катет AB прямоугольного треугольника находим по формуле
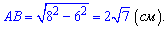
Ответ: Сторона трапеции равна 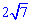 см.
см.
------------------------
Задача 7. В треугольнике АВС угол В = 90 градусов, ВD перпендикулярна АС, АВ = 16 см, ВС = 12 см. Найдите длину отрезка АD и тангенс угла при основании.
Решение. Рассмотрим вспомогательный рисунок к заданию.
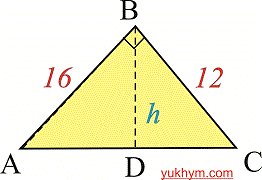
Составим пропорции для отыскания отрезка AD
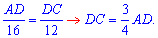
Второе уравнение построим на основе теоремы Пифагора
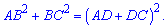
Думаю выше Вам все понятно. Следующим шагом подставляем DC и значение катетов в уравнение
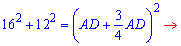
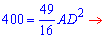
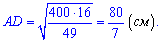
Отрезок найдено, тангенс угла А находим по формуле
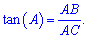
Определим длину гипотенузы - для этого найдем неизвестную часть DC
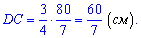
Гипотенуза равна сумме AD+DC
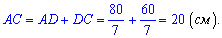
Вычислим тангенс угла при основании
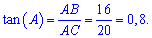
Ответ: AD=80/7, tan(A)=0,8.
------------------------
Задача 8. Периметр прямоугольного треугольника равен 12 см, а один из из его катетов - 3 см. Найдите площадь
треугольника.
Решение. Данный пример на сложение уравнения с неизвестными.
Первое уравнение соответствует формуле периметра треугольника, второе - теореме Пифагора.
Обозначим b – неизвестный катет, с – гипотенуза треугольника.
Составляем систему уравнений
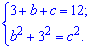
Имеем два уравнения с двумя неизвестными. Метод решения Вам известен: из первого уравнения выражаем одну из переменных и подставляем во второе. В результате после упрощений получим квадратное уравнение один из корней которого и будет решением. Второй получим в результате подстановки в первую зависимость системы уравнений.
У меня получилось что b=4 см, c=5 см.
Если не верите то можете пройти описанные выше процедуры.
Площадь находим как половину произведения катетов
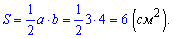
Ответ: площадь треугольника 6 сантиметров квадратных.
------------------------
Задача 9. Катеты прямоугольного треугольника равны 3 см и 4 см. Найти радиус вписанной и описанной окружности.
Решение. Радиус описанной окружности найти легче - он равен половине гипотенузы. Вычисляем ее длину по теореме Пифагора
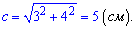
Отсюда находим больший радиус
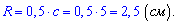
Радиус вписанной в прямоугольный треугольник окружности можно найти несколькими способами.
Пойдем простым и определим его на основе формулы площади треугольника
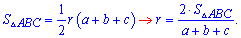
Как видите вычислить радиус вписанной окружности достаточно просто. Находим площадь треугольника
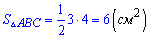
и подставляем в предыдущую формулу
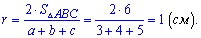
Вот такой сложный на восприятие пример легко решается при знании необходимых формул.
Ответ: радиусы описанной и вписанной окружности равны 2,5 см и 1 см соответственно.
------------------------
Изучайте формулы основных геометрических фигур, набирайтесь опыта на практике и со временем примеры будете решать без труда. Если же не удается решить пример или задачу, или непонятно условие задачи обращайтесь к специалистам. На этом сайте и подобных интернет ресурсах Вы всегда можете решить любую сложную задачу.
Посмотреть материалы
]]>
Свойства параллелограмма
Противоположные стороны параллелограмма как и противоположные углы равны между собой:
AB=CD, BC=AD,
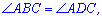
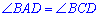
Диагонали параллелограмма в точке пересечения делятся на две равные части:
АО=OC, OB=OD.
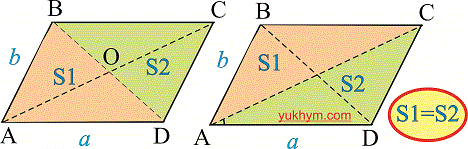
Углы прилегающие к любой стороне (соседние углы) в сумме равны 180 градусов.
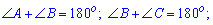
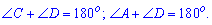
Каждая из диагоналей параллелограмма делит его на два одинаковые по площади и геометрическими размерами треугольники.
Еще одно замечательное свойство которое часто применяют при решении задач состоит в том, что сумма квадратов диагоналей в параллелограмме равна сумме квадратов всех сторон:
AC^2+BD^2=2*(AB^2+BC^2).
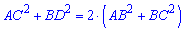
Основные признаки параллелограммов:
1. Четырехугольник у которого противоположные стороны попарно параллельны является параллелограммом.
2. Четырехугольник с равными противоположными сторонами является параллелограммом.
3. Четырехугольник с равными и параллельными противоположными сторонами является параллелограммом.
4. Если диагонали четырехугольника в точке пересечения делятся пополам то это параллелограмм.
5. Четырехугольник у которого противоположные углы попарно равны является параллелограммом
Биссектрисы параллелограмма
Биссектрисы противоположных углов в параллелограмме могут быть параллельными или совпадать.
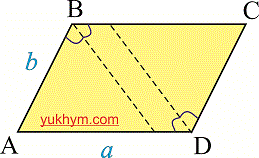
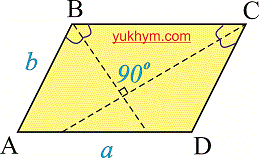
Биссектрисы соседних углов ( прилегающие к одной стороне ) пересекаются под прямым углом (перпендикулярные).
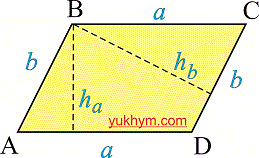
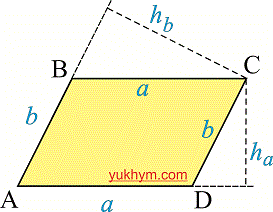
Высота параллелограмма
Высота параллелограмма — это отрезок который проведен с угла перпендикулярно к основанию. Из этого следует что из каждого угла можно провести две высоты.
Формула площади параллелограмма
Площадь параллелограмма равна произведению стороны на высоту проведенную к ней. Формула площади следующая
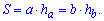
Вторая формула не менее популярная при вычислениях и определяется так: площадь параллелограмма равна произведению соседних сторон на синус угла между ними
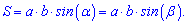
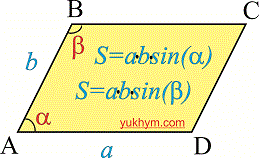
На основе приведенных формул Вы будете знать как вычислить площадь параллелограмма.
Периметр параллелограмма
Формула для вычисления периметру параллелограмма имеет вид
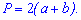
то есть периметр равен удвоенному значению суммы сторон. Задачи на параллелограмм будут рассмотрены в соседних материалах, а пока изучайте формулы. Большинство задач по вычислению сторон, диагоналей параллелограмма достаточно просты и сводятся к знанию теоремы синусов и теоремы Пифагора.
Посмотреть материалы:
]]>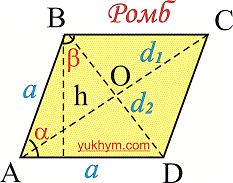
Свойства ромба
Поскольку ромб занимает некоторую часть параллелограммов то свойства в них будут похожими.
- Противоположные углы ромба как и параллелограмма равны.
- Сумма углов ромба прилегающих к одной стороне равна 180°.
- Диагонали ромба пересекаются под углом 90 градусов.
- Диагонали ромба являются одновременно биссектрисами его углов.
- Диагонали ромба в точке пересечения делятся пополам.
Признаки ромба
Все признаки ромба вытекают из его свойств и помогают различать его среди четырехугольников, прямоугольников, параллелограммов.
- Параллелограмм у которого диагонали пересекаются под прямым углом является ромбом.
- Параллелограмм у которого диагонали является биссектрисами является ромбом.
- Параллелограмм с равными сторонами является ромбом.
- Четырехугольник у которого все стороны равны является ромбом.
- Четырехугольник у которого диагонали является биссектрисами углов и пересекаются под прямым углом является ромбом.
- Параллелограмм с одинаковыми высотами является ромбом.
Формула периметра ромба
Периметр по определению равен сумме всех сторон. Поскольку в ромба все стороны равны то его периметр вычисляем по формуле
P=4a.
Периметр вычисляется в единицах длины.
Радиус окружности вписанной в ромб
Одними из распространенных задач при изучении ромба является нахождение радиуса или диаметра вписанной окружности. На рисунке изображенном ниже приведены одни из распространенных формул радиуса вписанной окружности в ромб.
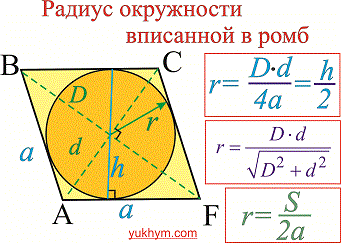
Первая формула показывает что радиус окружности вписанной в ромб равен произведению диагоналей разделенному на сумму всех сторон (4а).
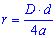
Другая формула показывает что радиус окружности вписанной в ромб равен половине высоты ромба
r=h/2.
Вторая формула на рисунке является модификацией первой и применяется при исчислении радиуса окружности вписанной в ромб когда известны диагонали ромба, то есть неизвестные стороны.
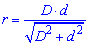
Третья формула радиуса вписанной окружности фактически находит половину высоты малого треугольника, который образуется пересечением диагоналей.
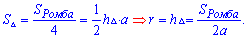
Среди менее популярных формул для вычисления радиуса окружности вписанной в ромб можно еще привести такие
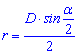
здесь D – диагональ ромба, alpha – угол который рассекает диагональ.
Если известна площадь (S) ромба и величина острого угла (alpha) то для вычисления радиуса вписанной окружности нужно найти квадратный корень из четверти произведения площади на синус острого угла:
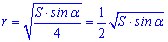
Из приведенных формул Вы без проблем найдете радиус вписанной в ромб окружности, если в условиях примера будут необходимый набор данных.
Формула площади ромба
Формул для вычисления площади приведены на рисунке.
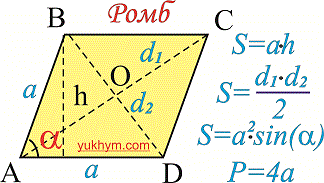
Простейшая выводится как сумма площадей двух треугольников на которые разделяет ромб его диагональ.
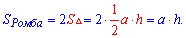
Вторая формула площади применяется к задачам в которых известны диагонали ромба. Тогда площадь ромба равна половине произведению диагоналей
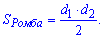
Она достаточно проста для того чтобы запомнить, а также - для вычислений.
Третья формула площади имеет смысл когда известен угол между сторонами. Согласно ей площадь ромба равна произведению квадрата стороны на синус угла. Острый он или нет значения не имеет поскольку синус обоих углов принимает одинаковое значение.
Периметр ромба
Периметр ромба равен сумме всех его сторон. Учитывая то что они все равны периметр принимает значение
P=4a.
И в завершение запомните что периметр измеряется в единицах длины, а площадь в квадратных единицах. Теперь Вы знаете как найти площадь и периметр ромба, поэтому пользуйтесь приведенным формулам при решении задач.
Посмотреть материалы:
]]>Формулы площади трапеции
1. Площадь трапеции равна произведению полусуммы основ на высоту:
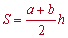
Средняя линия трапеции равна полусумме оснований, таким образом предыдущую формулу площади можно записать в виде
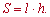
Ниже на рисунке приведены соответствующие формулы и обозначения
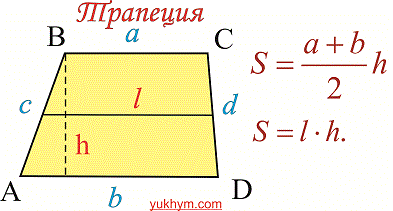
2. Если задано диагонали трапеции и угол между ними (смотрите рисунок )
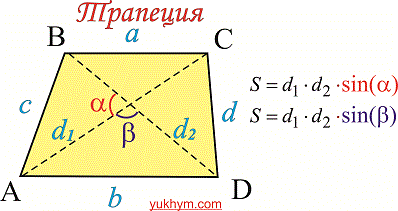
то площадь трапеции находят по формуле
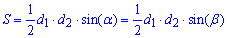
Данная формула, как и предыдущая, достаточно проста в вычислениях.
Следующая формула требует большего количества расчетов.
3. Бывают сложные примеры на трапецию когда задано все четыре ее стороны. В таких случаях используют первую формулу площади трапеции
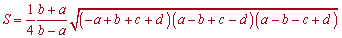
или вторую
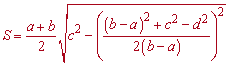
При применении формулы следует помнит, что между сторонами должны выполняться условия b>a и c>d.
4. Если в задании известно что трапеция равнобедренная (боковые стороны равны ) то для того, чтобы найти площадь трапеции кроме выше приведенных формул используют следующие:
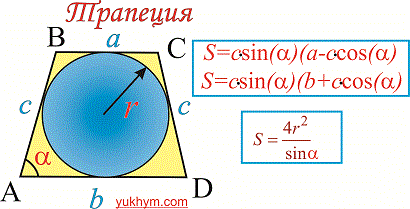
- если задано основу, боковую сторону и угол между ними
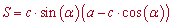
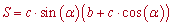
- если известен радиус вписанной окружности и угол при основании
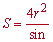
Здесь r – радиус окружности, alpha – угол при основании, c – боковая сторона равнобокой трапеции.
Если радиус вписанной окружности и нужен угол не известны в условии задания - пользуйтесь выше приведенным формулам площади трапеции.
Теперь Вы знаете как найти площадь трапеции – используйте приведенные формулы на практике и не питайте проблем в обучении.
Посмотреть материалы:
]]>