При розв'язанні задач теорії ймовірностей, що призводять до застосування формул Бернуллі і Лапласа часто використовують поняття найімовірнішого числа здійснення подій.
Нехай маємо n незалежних випробувань, в яких подія A з'являється з однаковою ймовірністю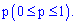 
Завдання полягає у відшуканні найвірогіднішого числаk0здійснення події A в цих випробуваннях (байдуже в якій послідовності). Виведення цієї умови подавати ми Вам не будемо, а лише запишемо її у вигляді подвійної нерівності
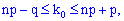де q=1-p. Якщо говорити термінами теоріїї ймовірності, то найімовірніше число k0 появи випадкової події віповідає значенню, при якому ймовірність приймає максимальне значення
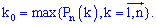Таких чисел може бути не більше двох.
Правила визначення найвірогіднішого числа здійснення події
1. Спочатку обчислюємо значення n*p, якщо воно – ціле число, то отримаємо
k0=n*p.
2. Визначаємо суму n*p+p і якщо вона ціле число, то існує два найімовірніших числа
k0=n*p+p; k1=k0-1=n*p+p-1.
3. Якщо n*p+p неціле число, то k0 визначаємо як єдине ціле число з проміжку
[n*p-q; n*p+p].
Розв'яжемо декілька задач для закріплення теми.
Приклад 1. Ймовірність того, що професійний футболіст не влучить із середини поля у ворота противника дорівнює 0,02. Знайти найвірогідніше число промахів у площину воріт при 300 спробах.
Розв'язання. Проводять n=300 незалежних випробувань з однаковою ймовірністю появи події A (невлучання у площину воріт) в кожному з них (p=0,02; q=0,98). Найвірогідніше число здійснення події A визначаємо з нерівності
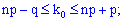
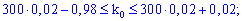
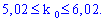
Найвірогідніше число здійснення подій – це завжди ціле число. Тому шукане значення рівне k0=6.
Приклад 2. У партії однотипних деталей кількості стандартних і бракованих відносяться як 5:4. Навмання з партії беруть 9 деталей.
Знайти найімовірніше число k0 появи нестандартних деталей серед 9 навмання взятих і обчислити відповідну ймовірність.
Розв'язання: Ймовірності вибрати стандартну чи браковану деталь обчислимо з їх пропорції 5:4.
p=5/(5+4)=5/9; q=4/9.
Найімовірніше число появи стандартних деталей знайдемо за формулою
n•p-q≤k0≤n•p+p.
9•5/9-4/9<k0<9•5/9+5/9
5-4/9<k0<5+5/9 k0=5.
Закон розподілу ймовірностей знаходимо за формулою Бернуллі
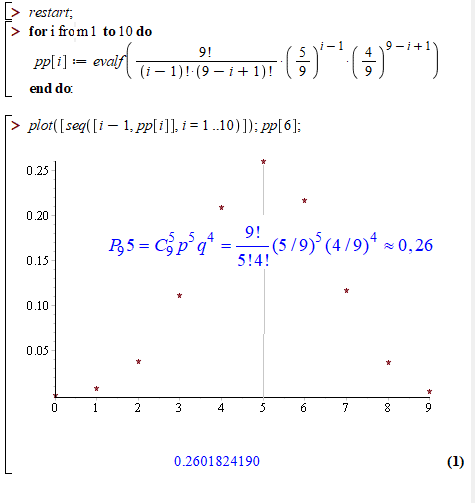
Вище наведено фрагмент коду в мат. пакеті Мейпл17 для побудови закону розподілу ймовірностей.
За формулою Бернуллі обчислюємо P9(5):
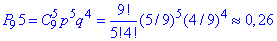
Можете співставити з максимумом на графіку, це і є шукана ймовірність при к0=5.
Приклад 3. Імовірність виграти за лотерейним білетом рівна 0,03. Яке найвірогідніше число виграшних білетів із 99?
Скільки потрібно купити білетів, щоб серед них найімовірніше число виграшних білетів було рівне одиниці?
Розв'язання. Проводять n=99 незалежних випробувань із ймовірністю успіху у кожному ( p=0,03). Найвірогідніше число здійснення події A визначаємо із подвійної нерівності
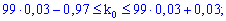
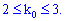
Отримали випадок, який дуже рідко зустрічається. Два числа 2,3 - кількості білетів, які мають однакову вірогідність появи.
Для відповіді на другу половину завдання потрібно розв'язати дві нерівності: в них k0 задане і рівне 1; потрібно знайти краї проміжку
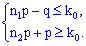
Підставляємо відомі значення
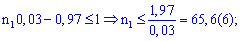
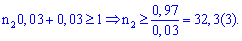
Числа n1, n2 повинні також бути цілими, тому потрібно купити не менше 32 білетів і не більше 65.
Приклад 4. Скільки треба взяти деталей, щоб найвірогідніше число придатних було рівно 25, якщо ймовірність того, що навмання взята деталь виявиться бракованою дорівнює 0,25 ?
Розв'язання. Ймовірність того, що деталь є придатною, визначимо як ймовірність протилежної події: p=1-0,25=0,75. Для визначення шуканої величини n застосуємо формулу найвірогіднішого числа здійснення подій, та підставивши в неї значення k0=25 і p=0,75 матимемо нерівності
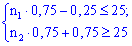
Розв'язавши систему нерівностей, отримаємо краї проміжку:
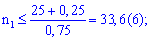
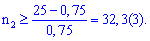
Єдиним значенням, що задовільняє обидві умови буде число 33.
Приклад 5. Знайти найімовірніше число лекцій, які відвідав студент з 75 запланованих за рік якщо ймовірність відвідування кожної лекції дорівнює 0,85.
Розв'язання. За умовою маємо n=75; p=0,85; q=1-p=0,15. Застосовуємо формулу найвірогідніого числа появи подій в схемі Бернуллі
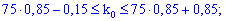
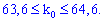
З останнього запису знаходимо, що студент з 75 лекцій найімовірніше відвідав 64.
Приклад 6. Скільки мінімально потрібно підкинути гральний кубик, щоб найімовірніше число випадання п'яти очок було рівне 6?
Розв'язання. Ймовірність випадання п'яти очок вважаємо незалежною подією з ймовірністю появи p=1/6, оскільки граней 6 і тільки на одній п'ятірка. Протилежна подія матиме ймовірність q=1-1/6=5/6. За відомою формулою отримаємо нерівності
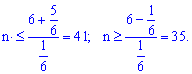
Найменшим числом із заданого проміжку є 35. Отже гральний кубик потрібно підкинути мінімум 35 разів.
Подібних прикладів на практиці Ви зустрінете чимало, тому запам'ятайте формулу найвірогіднішого числа подій та використовуйте її там де потрібно. Визначення найімовірнішого числа в схемі Бернуллі досить просте математично, тому помилки при обчисленнях не повинні виникати.
