Основна суть локальної та інтегральної теореми Лапласа детально описана на попередньому уроці. Далі наведені відповіді до типових задач з ймовірності та приведено код в Мейплі, який допоможе автоматизувати знаходження імовірності з допомогою формул локальної та інтегральної функцій Лапласа. Постійне розв'язування однотипних завдань вимагає користування довідниками ()онлайн чи ні), тому прості приклади краще вчитися програмувати в математичних пакетах.
Спершу розглянемо приклади, які багатьом з Вас зустрічалися, частина студентів шукає в інтернеті.
Задача 3. Пристрій складається з трьох незалежних елементів, що працюють протягом часу T безвідмовно, відповідно з ймовірностями
p1=0,861; p2=0,761; p3=0,711.
Знайти ймовірність того, що за час T вийде з ладу:
а) тільки один елемент
б) хоча б один елемент
Обчислення: а) Подія «з ладу вийде тільки один елемент» означає, що або перший, або другий, або третій елементи пристрою вийдуть з ладу. «або» на мові ймовірності відповідає за сумування ймовірностей
p=p1•q2•q3+q1•p2•q3+q1•q2•p3 (1)
Обчислимо ймовірності протилежних подій
q1=1-p1=1-0,861=0,139
q2=1-p2=1-0,761=0,239
q3=1-p3=1-0,711=0,289
Підставляємо в формулу (1)
p=0,861•0,239•0,289+0,139•0,761•0,289+0,139•0,239•0,711≈0,031
б) Подія "з ладу вийде хоча б один елемент" означає, що від одного до трьох елементів вийде з ладу. Така подія є протилежною до того, що жоден елемент не вийде з ладу, тому ймовірність легше обчислювати як різницю між повною ймовірністю та ймовірністю, що жоден елемент не вийде з ладу. Імовірність, що жоден елемент не вийде з ладу знаходимо за формулою
p(0)=p1•p2•p3=0,861•0,761•0,711≈0,46586
Обчислюємо ймовірність, що з ладу вийде хоча б один елемент
p=1-p(0)=1-0,46586≈0,5341
Відповідь: 0,031; 0,5341.
Це завдання на повну групу подій, і такі завдання розв'язують без використання формул Лапласа.
Задача 4 Ймовірність виходу з ладу за час t одного приладу дорівнює p=0.5.
Визначити ймовірність того, що за час t з n=60 приладів вийдуть з ладу:
а) рівно k1=35 приладів;
б) від k2=25 до k3=32 приладів;
в) не менше k4=33 приладів;
г) менше k5=26 приладів.
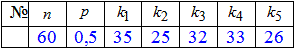
Розв'язання: а) Найточніше значення ймовірності, що вийде з ладу рівно 35 приладів з 60 дає формула Бернуллі
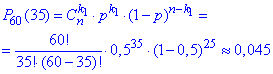
Це варто знати, оскільки і такі питання можуть бути на екзамені, тестах, модулях.
Наближене значення можна знайти через локальну теорему Лапласа.
Оскільки необхідна умова її застосування k= n•p•q=60•0.5•0.5=15>9 виконується, то похибка наближених формул мінімальна

Виконаємо обчислення "ікса":
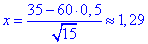
За таблицями табулювання локальної функції Лапласа знаходимо значення "фі" в точці

За першою з формул знаходимо ймовірність
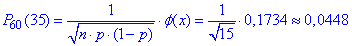
Порівнюючи значення 0.045 та 0.0448 робимо висновок про достатньо добру точність наближених формул Лапласа.
Але такий висновок не завжди справедливий, і в цьому Ви переконаєтесь з наступних обчислень.
б) За інтегральною формулою Лапласа знайдемо ймовірність, що від 25 до 32 приладів із 60 вийдуть з ладу :
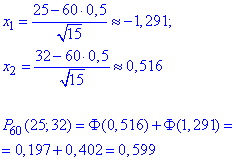
Знаходження точок не важке, складніше в таблиці знайти значення функції "Фі".
Точне значення знайдене через формулу Бернуллі в мейплі рівне
p:= 0.6630200464
Для цього нам довелося написати всього три рядки коду, причому можна було обійтися без першого
restart;
P:=(p,n,k)->n!/k!/(n-k)!*p^k*(1-p)^(n-k);
> p1:=sum(P(0.5,60,s),s=25..32);
p1 := 0.6630200464
Фрагмент програми наведено далі
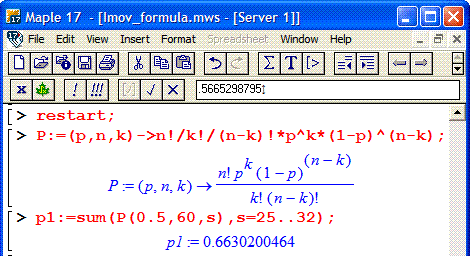
в) Ймовірність, що не менше 33 приладів зі 60 вийдуть з ладу обчислимо за інтегральною теоремою Лапласа.
Запам'ятайте, що локальна теорема Лапласа служить для знаходження одного значення.
Інтегральна функція Лапласа - ймовірності з проміжку, наприклад "не менше, не більше" з n, а це свою чергу вимагає відшукання великої кількості значень за формулою Бернулі, або ту ж саму кількість за локальною теоремою Лапласа, що є неправильно та веде до росту похибки.
Тому тут знаходимо "ікси", та за їхнім значенням функції "Фі"
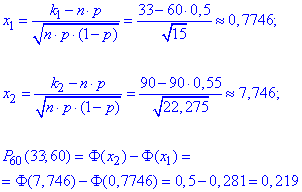
Точне значення ймовірності знайдене в Мейпл рівне
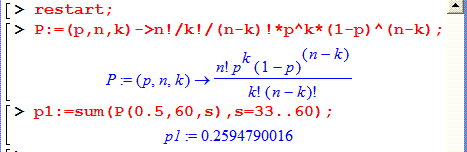
г) Імовірність, що менше 26 приладів вийдуть з ладу означає, що від 0 до 26 з 90.
Виконуємо обчислення за інтегральною теоремою Лапласа:
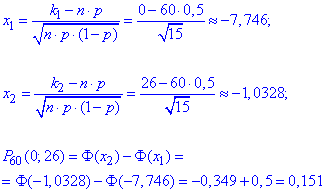
Точне значення нам знову допоможе знайти фунція Бернуллі

Розглянемо останній приклад після якого наведемо формули Лапласа в мейплі та порівняємо отримані значення.
Задача 5 Ймовірність виходу з ладу за час t одного приладу дорівнює p=0.4.
Визначити ймовірність того, що за час t з n=95 приладів вийдуть з ладу:
а) рівно k1=40 приладів;
б) від k2=35 до k3=45 приладів;
в) не менше k4=42 приладів;
г) менше k5=38 приладів.
У ВУЗах завдання звучать без значень, а в окремих таблицях значення для кожного варіанту.
Таким чином умова спільна, а завдання на модуль чи розрахункову для кожного студента індивідуальні.
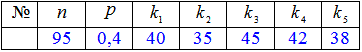
Розв'язання: а) За формулою Бернуллі визначаємо ймовірність, що вийде з ладу рівно 50 приладів з 90
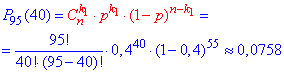
За локальною теоремою Лаплас обчислимо наближене значення.
Оскільки необхідна умова виконується k=95•0.4•0.6=22.8>9, то розходження з точним значенням незначне.
Знаходимо "ікс":
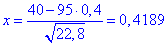
За таблицями табулювання локальної функції Лапласа маємо "фі", а далі визначаємо ймовірність 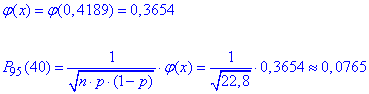
Розбіжність між точним значенням та наближеним невелика.
Знаходження ймовірностей в Мейплі. Локальна та інтегральна теорема Лапласа
Напишемо кіька рядків коду для обчислення лоальної функції Лапласа в мейплі. Код надто простий, щоб в ньому щось коментувати, єдине зауважимо, що функція evalf() застосовується для оруглення, щоб ми на екрані не бачили радикалів (коренів).
> x:=(p,n,k)->(k-n*p)/sqrt(n*p*(1-p));
> phi:=x -> 1/sqrt(2*Pi)*exp(-x^2/2);
> P1:=(n,p,phi)->phi/sqrt(n*p*(1-p));
Далі для обчислень імовірності знаходимо значення фунцій відповідно до умов пункту а)
>x1:=x(0.4,95,40);
x1 := 0.4188539082
>phi_1:=evalf(phi(x1));
phi_1 := 0.3654382971
>p_1:=P1(95,0.4,phi_1);
p_1 := 0.07653262948
Фрагмент програми наведено на рисунку

б) Ймовірність, що від 35 до 45 приладів із 95 вийдуть з ладу знайдемо за інтегральною формулою Лапласа:
Обчисимо два "ікси", що відповідають за крайні точки інтервалу, а далі за таблицями інтегральної фунції "Фі" обчислимо ймовірність.
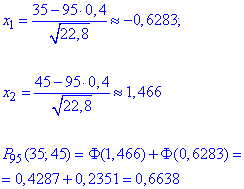
Отже, наближене значення рівне 0.6638, точне
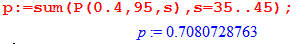
Похибка наближених розрахунків невелика.
в) Ймовірність, що не менше 42 приладів з 95 вийдуть з ладу обчислимо за інтегральною теоремою Лапласа: 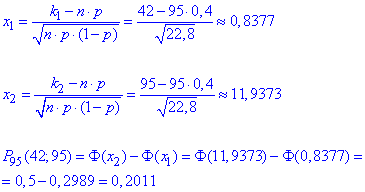
Тточне значення імовірності
p := 0.2308769403
г) Ймовірність, що менше 38 приладів вийдуть з ладу означає, що від 0 до 38.
За інтегральною теоремою Лапласа знаходимо "ікси", а далі "Фі" в цих точках:
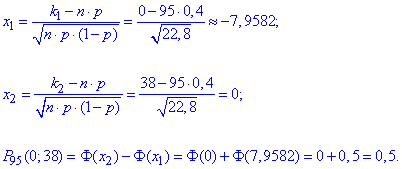
Ймовірність 50 на 50.
За формулою Бернуллі знаходимо точне значення
p :=0 .5444118318
Обчислення ймовірності в Мейплі. Інтегральна теорема Лапласа
Запишемо код інтегральної функції Лапласа в Мейплі
>x_i:=(p,n,k)->(k-n*p)/sqrt(n*p*(1-p));
> Phi:=x->1/sqrt(2*Pi)*int(exp(-t^2/2),t=0..x);
Якщо порівняти, то "ікси" обчислюємо за тією ж формулою, що і в локальній теоремі.
Далі знаходимо імовірність, що менше 38 з 95 приладів вийдуть з ладу
x1:=x_i(0.4,95,0);x2:=x_i(0.4,95,38);
x1 := -7.958224257
x2 := 0.
> Phi_1:=evalf(Phi(x1));Phi_2:=Phi(x2);
Phi_1 := -0.4999999997
Phi_2 := 0.
p:=Phi_2-Phi_1;
p := .4999999997
Тут вже добавити нічого, хіба що скріншот з мейпла

А тепер подумайте; Чи потрібно вчити математичні пакети у ВУЗах?


