Задачі з теорії ймовірностей на кульки

Завдання в яких потрібно знайти ймовірність вибрати рівно m з n речей, не менше m з n, хоча б m з n за умови, що є речі з іншими властивості (кульки іншого кольору, браковані деталі, кольорові лампочки, телефон і т.д.) часто можна зустріти на практиці, модулях та контрольних з ймовірності. Вони не важкі в плані обчислень, потрібно знати одну формулу з комбінаторики (сполучення) та вміти спрощувати факторіали.
Інший спосіб знайти ймовірність, який Ви можете використовувати в роботі після закінчення ВУЗів, або для самоперевірки вдома - це написання програм (скриптів) в математичних пакетах, які більш швидші та унеможливлюють виконання помилок при правильно написаному коді. Плюс до того - це свого роду підготовка до програмування, яке так швидко розвивається та охоплює всі можливі галузі. Про це все піде мова далі, тому читайте і застосовуйте на практиці.

Задача 1. В урні 5 чорних і 6 білих кульки. Випадково виймають 5 кульок. Знайти ймовірність того, що серед них є:
а) 3 білі кульки;
б) менше, ніж 3, білих куль;
в) хоча б одна біла кулька;
Обчислення: а) Число всіх можливих подій в даній задачі це кількість способів, за якими можна вибрати 5 кульки із (6+5) =11. Обчислюємо через формулу сполучень без повторень

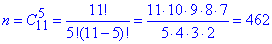
Число сприятливих подій рівне добутку:

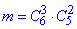
де 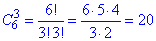- кількість способів, за якими можна вибрати 3 білих кульки з 6;
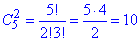- кількість способів, за якими можна вибрати 5-3=2 чорних кульки з 5.
Ймовірність події A, при якій виймають 3 кульки білого кольору рівна частці:
P(A)=m/n=20•10/462≈0,4329

б) Ймовірність вибрати менше, ніж 3 білих куль кульки означає або 0, або 1, або 2. На мові формул це сума ймовірностей p(0), p(1), p(2) (пояснення ті самі, що і в попередніх пунктах):

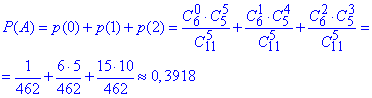
в) Імовірністьвибратихочабоднубілукулькуєпротилежноюдоймовірностівибрати 5 кульокчорногокольору, тому:

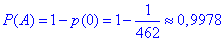
Ценайпростішийспосіб, оскількинемаємосумибагатьохдоданків.
Відповідь: а) 0,4329; б) 0,3918; в) 0,9978.

Задача 2. В одній урні K=5 білих і L=5 чорних кульок, а в другій урні N=4 білих і M=8 чорних кульок. З першої урни навмання виймають 2 кульки, а з другої 2. Знайти ймовірність того, що серед вийнятих куль будуть:
а) усі кулі одного кольору;
б) тільки 3 білих кульки;
в) хоча б одна біла кулька.
Обчислення: Завдання такого типу ми віднесли до задач на кульки, хоча їх можна було об'єднати в окрему статтю. Запам'ятайте алгоритм обчислень та застосовуйте для аналогічних прикладів.
а) В першій урні 5+5=10 кульок і в другій 4+8=12. Вийняти усі кулі одного кольору, означає що потрібно вийняти або 4 чорні, по дві з кожної урни, або 4 білі. У ймовірності «або» відповідає за суму ймовірностей.
Порядок вибору не має значення, тому ймовірність вийняти білу кульку з першого ящика рівна 5/10, з другого – 4/12. Після цього в першій урні залишиться 9 куль з яких 4 білі, в другій 11 куль, з яких 3 білі. Ймовірності їх вийняти рівні 4/9, та 3/11 відповідно, а ймовірність вийняти 4 білі кулі рівна
p1=5/10•4/9•4/12•3/11≈0,0202
Для 4 чорних куль ймовірність вийняти їх з першої та другої урни рівні 5/10 та 8/12 відповідно, після цього в 1 урні буде 9 куль, 4 з яких чорні. В другій залишиться 7 чорних куль з 11. Тому ймовірності вийняти за другим разом чорні кулі рівні 4/9 та 7/11 відповідно. А ймовірність вибрати 4 чорні кулі з двох урн рівна
p2=5/10•4/9•8/12•7/11≈0,0943
Сумарна ймовірність рівна
p=p1+p2≈0,0202+0,0943≈0,1145

б) Ймовірність вийняти 3 білих з 4, при умові що з кожної урни беруть по дві кульки рівносильна, що з першої виймуть 2 білі і з другої одну, або з першої одну білу, а з другої дві білі.
Перший варіант можливий з ймовірністю
p1=5/10•4/9•4/12•8/11≈0,05387
другий з імовірністю
p1=5/10•5/9•4/12•3/11≈0,02525
Ймовірність вийняти тільки 3 білі кулі рівна
p=p1+p2=0,05387+0,02525≈0,079122

в) хоча б одна біла кулька, означає або одна або дві або три або чотири. Це багато обчислень, тому краще від повної ймовірності відняти ймовірність протилежної події = жодної білої кульки. Обчислюємо
p=1-5/10•4/9•8/12•7/11≈0,9057
Відповідь: 0,1145; 0,079; 0,9057.

Задача 3. В урні 6 білих і 23 чорні кульки. З урни навмання виймають 4 кульки. Знайти ймовірність того, що серед них будуть:

а) 3 білі кульки;
б) 3 чорні кульки;
в) 3 білих або 3 чорних кульки;
г) 2 білих і 2 чорних кульок;
д) не більше ніж 3 білі кульки;
е) не менше ніж 3 чорні кульки;
є) хоча б одна біла кулька;
ж) кульки одного кольору.

Розв'язання: Наведені далі пояснення є спільними для всіх задач з подібними умовами. Це можуть бути карти, кубики, деталі, машини, телефони і т. д.
Головне тут умови, які перелічені в пунктах а-ж.
а) Згідно головного і самого зрозуміого означення ймовірність рівна частці сприятливих подій до всіх можливих.
Число всіх можливих подій в даній задачі це кількість способів, за якими можна вибрати 4 кульки із 29 (6+23)
n=C₂₉⁴.
Число сприятливих подій рівне добутку:
m=C₆³·C₂₃¹=460,
де C₆³ - кількість способів, за якими можна вибрати 3 білих кульки з 6;
C₂₃¹- кількість способів, за якими можна вибрати 1 чорну кульку з 23.
Ймовірність події A, при якій виймають 3 з 6 кульки білого кольору рівна частці:

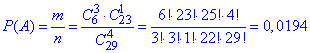
З пояснеь ніби все просте і зрозуміле, проте як показує практика не всі студенти це розуміють, а ще є таке як "лінь" вчити. Тому все буде багатократно повторювати та розбирати до дрібниць.

б) Число всіх можливих подій за якими можна вибрати 4 кульки із 29 стале для всіх пунктів і рівне
n=C₂₉⁴=23751.
Число сприятливих подій:
m=C₂₃³·C₆¹=10626
де C₂₃³ - кількість способів, за якими можна вибрати 3 чорних кульки з 23;
C₆¹- кількість способів, за якими можна вибрати 1 білу кульку з 6.
Ймовірність події B, при якій виймають 3 з 23 кульки чорного кольору рівна 0.4474:

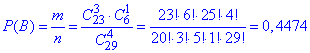
В попередньому пункті та всюди далі застосовуємо формулу C_n^m=n!/m!/(n-m)! оскільки нам не важливо, яка з кульок буде вибрана першою, а яка остатньою. Тут порядок вхлдження не важливий. Там де порядок важливий сід використовувати A_n^m=n!/m!

в) Ймовірність вибрати 3 білих або 3 чорних кульок – це сума ймовірностей p(A) і p(B): p=p(A)+p(B)=0,0194+0,4474=0,4668.
Подумайте, чому саме так?

г) Ймовірність вибрати 2 білих і 2 чорних кульки рівна 0.1598:

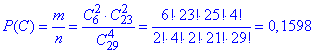
тут C₆² - кількість варіантів вибрати 2 білих кульки з 6;
C₂₃²- кількість всеможливих способів вибрати 2 чорних кульки з 23.

д) Ймовірність вибрати не більше ніж 3 білих кульки означає або 0, або 1, або2, або 3 серед усіх.
На мові формул це сума ймовірностей p(0), p(1), p(2), p(3) (пояснення ті самі, що і в попередніх пунктах):

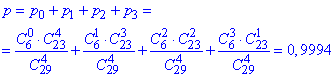
е) Ймовірність вибрати не менше ніж 3 чорних кульки означає або 3, або 4.
Це сума ймовірностей p(3), p(4), тому знаходимо за формулою:

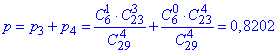
є) Імовірність вибрати хоча б одну білу кульку є протилежною до ймовірності вибрати 4 кульки чорного кольору, тому:

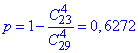
Це найпростіший спосіб, оскільки не маємо суми багатьох доданків, а лише від повної імовірності (=1) віднімаємо ймовірність протилежної події.

ж) Ймовірність вибрати кульки одного кольору означає вибрати або 4 з 6 білих кульок, або 4 з 23 чорних кульок:

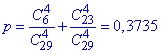
Щоб наведені відповіді не були для Вас примітивими та без практичного застосування наведемо алгоритм, як знайти ймовірності в Мейплі. Це нескладно + стане в нагоді для всіх хто вчить математичні програми, хоче знати щось нове, займається репетиторством, чи немає бажання марнувати часу для обчислень на калькуляторі.
Матеріал також буде корисним і студентам чи викладачам, які виконують курсові та модулі з ймовірності на замовлення.
>restart: дана команда занулює (очищає память) всі значення, що були попередньо присвоєні.
Далі створюємо фунцію, щоб кожного разу не писати дробові функції з фаторіалами.
> C:=(n,m)-> n!/m!/(n-m)!;
Далі обчислюємо чисельники та знаменники, які фігурують в прикладах та саму ймовірність настання події.
> n:=C(29,4);
n := 23751

> m1:=C(6,3)*C(23,1);
m1 := 460

> p1=evalf(m1/n);
p1 = 0.01936760557

> m2:=C(23,3)*C(6,1);
m2 := 10626

> p2=evalf(m2/n);
p2 = 0.4473916888

> m3:=C(6,2)*C(23,2);
m3 := 3795

> p3:=evalf(m3/n);
p3 := 0.1597827460

Тут Ви отримаєте задовільну точність обчислень і можливість контролювати відповіді.
При бажанні можете написати скрипти, які за одну дію дають відповідь на будь-який з пунктів завдання. Для цього спробуйте побудувати функцію, яка в свою чергу викликає C(n,m). Поекспериментуйте і Вам обов'язково сподобається розв'язувати задачі з теорії ймовірностей в Мейплі.
Вікно з результатами компіляції наведено далі

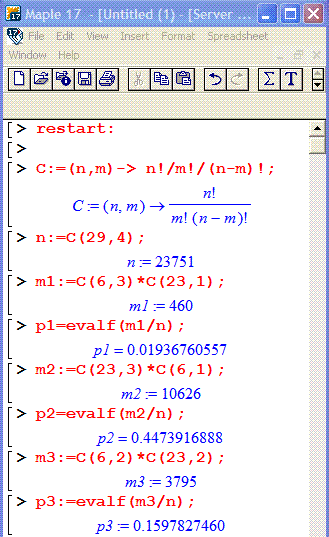
Розглянемо ще дві задачі, які задавали на модулі з теорії ймовіності.

Приклад 2 В урні 7 білих і 24 чорні кульки. З урни навмання виймають 5 кульок. Знайти ймовірність того, що серед них будуть:

а) 4 білі кульки;
б) 4 чорні кульки;
в) 4 білих або 4 чорних кульок;
г) 2 білі і 3 чорні кульки;
д) не більше ніж 4 білі кульки;
е) не менше ніж 4 чорні кульок;
є) хоча б одна біла кулька;
ж) кульки одного кольору.

Значення параметрів для варіанту наведено в таблиці

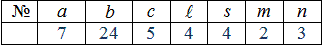
Розв'язання: Схема розрахунків ідентична до першої задачі, однак повторення необхідне, щоб дехто можливо зрозумів особливі моменти, які не завжди легко усвідомити з одного наведого прикладу.
а) Знаходимо знаменник – кількість способів, за якими можна вибрати 5 кульок із 31 (7+24)
n=C₃₁⁵ =169911.
Число сприятливих подій через добуток:
m=C₂₄¹·C₇⁴=24·C₇⁴=840.
де C₇⁴ - кількість способів, за якими можна вибрати 4 білих кульок з 7;
C₂₄¹- кількість способів, за якими можна вибрати 1 чорну кульку з 24.
Ймовірність події A, при якій виймають 4 з 5 кульки білого кольору рівна m/n=0.0049:

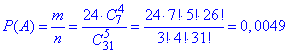
б) Число сприятливих подій для умови рівне:
m=C₂₄⁴·C₇¹=7·C₂₄⁴=74382
де C₂₄⁴ - кількість способів, за якими можна вибрати 4 чорних кульки з 5;
C₇¹ - кількість способів, за якими можна вибрати 1 білу кульку з 5.
Імовірність дістати 4 з 5 кульки чорного кольору серед усіх інших комбінацій рівна 0.4377:

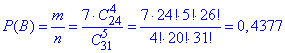
в) Ймовірність вибрати 4 білих або 4 чорних кульок з 5 – це сума знайдених в попередніх двох пунктах значень p(A) і p(B):
p=p(A)+p(B)=0,0049+0,4377=0,4426.

г) Далі знаходимо імовірність вийняти 2 білі і 3 чорні кульки з 5:

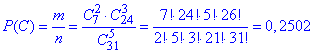
де C₇² - кількість способів, за якими можна вибрати 2 білі кульки з 7;
C₂₄⁴- кількість способів, за якими можна вибрати 3 чорні кульки з 24.
Думаю коментарів достатньо, як і пояснень чому саме так, а не інакше!

д) Імовірність вибрати не більше ніж 4 білі кульки є подією, яка протилежна до події витягнути всі 5 білих кульок, тобто

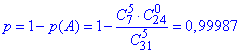
е) Імовірність вибрати не менше ніж 4 чорні кульки означає або 4 з 5 або всі 5.
Це сума ймовірностей p(4), p(5) (пояснення аналогічні до попередніх пунктів):

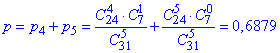
є) Ймовірність дістати хоча б одну білу кульку є протилежною до ймовірності вибрати 5 кульок чорного кольору, тому:

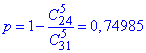
Поміркуйте, які варіанти можливі при 5 кульках і Ви зрозумієте чому так, та ще отримаєте багато корисних висновків, про які мало хто хоче наголошувати в теорії.

ж) Імовірність вибрати кульки одного кольору означає вибрати або 5 з 7 білих кульок, або 5 з 24 чорних кульок, а це рівне сумі ймовірностей:

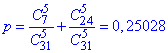
Ще одне завдання розв'язано. Думаю всым все зрозуміло і можемо розглянути нове завдання, яке в цій публікації останнє. Більше подібного змісту завдань шукайте в сусідніх статтях або в розділі контроьних робіт з ймовірності.

Приклад 3 В урні a=16 білих і b=12 чорних кульок. З урни навмання виймають c=9 кульок. Знайти ймовірність того, що серед них будуть:

а) l=4 білих кульок;
б) s чорних кульок;
в) l=4 білих або s чорних кульок;
г) m=6 білих і n=3 чорних кульок;
д) не більше ніж l=4 білих кульок;
е) не менше ніж s=7 чорних кульок;
є) хоча б одна біла кулька;
ж) кульки одного кольору.

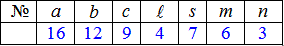
Розв'язання:Повторення матеріалу це найкращий спосіб знайти або помилку або щось нове.
а) Знаходимо сисло всіх можливих способів, за якими можна вибрати 9 кульок із 28=16+12 рівне
n=C₂₈⁹ =6906900.
Далі через два множники обчислюємо число сприятливих подій:
m=C₁₆⁴·C₁₂⁵=1441440
де C₁₆⁴- кількість способів, за якими можна вибрати 4 білих кульок з 16;
C₁₂⁵- кількість способів, за якими можна вибрати 5 чорних кульок з 12.
Імовірність події A, при якій виймають 4 з 9 кульки білого кольору рівна 0.2087:

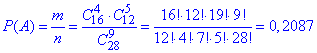
Тут розписані факторіали, ми їх спрощуємо легко. Хто має труднощі з факторіалами починайте з легих завдань та по мірі знань переходіть до важчих.

б) Число сприятливих подій вийняти 7 чорних кульок з 9 рівне:
m=C₁₂⁷·C₁₆²=95040
де C₁₂⁷ - кількість способів вибрати 7 чорних кульок з 12;
C₁₆²- кількість варіантів дістати 2 білі кульки з 16.
Ймовірність події B, при якій виймають 7 з 9 кульок чорного кольору рівна 0.0138:

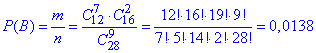
в) Імовірність вибрати 4 білих або 7 чорних кульок з 9 – це сума попередньо знайдених величин p(A) і p(B):
p=p(A)+p(B)=0.2087+0.0138=0.2225.

г) Знайдемо імовірність вибрати 6 білих і 3 чорних кульок з 9:

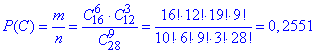
де C₁₆⁶ - кількість способів, за якими можна вибрати 6 білих кульок з 16;
C₁₂³- кількість способів, за якими можна вибрати 3 чорних кульок з 12.

д) Імовірність вибрати не більше ніж 4 білі кульки означає або 0, або 1, або 2, або 3, або 4 з 9.
Це сума ймовірностей p(0), p(1), p(2), p(3), p(4) (пояснення на основі вивченого раніше):

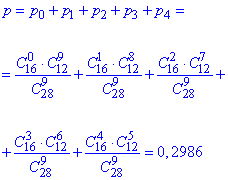
е) Ймовірність вибрати не менше ніж 7 чорних кульок означає від 7 до 9 з 9.
Це сума трьох доданів p(7), p(8), p(9) які знаходимо за формулою:

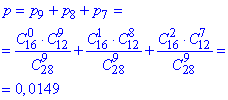
є) Імовірність вибрати хоча б одну білу кульку є протилежною до ймовірності вибрати 9 кульок чорного кольору, тому:

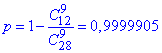
ж) Імовірність отримати всі кульки одного кольору означає вибрати або 9 з 16 білих кульок, або 9 з 12 чорних кульок:

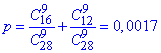
Як я обіцяв - це останнє завдання, решта готових відповідей в наступному матеріалі.

З наведених пояснень можна переконатися завдання не складні, якщо мати детальну інструкцію перед очима.
Вам також допоможе знання математичних пакетів, їх безліч, тому який краще вчити обирайте самостійно.
І пам'ятайте, що тільки практика та самоосвіта допоможуть Вам зрозуміти, що за що відповідає, і як правильно читати (трактувати) запитання в умові задачі.