Пригадаємо основні правила за якими виконують вибір тієї чи іншої комбінаторної формули в обчисленнях. Вам необхідно їх вивчити, щоб вільно застосовувати на практиці та не тлумачити як захочеться формули розміщень, перестановок та комбінацій.
Елементи комбінаторики
Вибір формули для обчислення сполук
Відомі два базові правила, за якими приймають рішення:
якою формулою комбінаторики слід користуватися?
Чи це будуть комбінації, перестановки чи розміщення залежить від відповіді на два питання.
1) Чи враховується порядок розміщення елементів?
Якщо відповідь «ні» то застосовуємо формулу комбінацій.
Якщо «так», то маємо два варіанти, які залежать від відповіді на наступне питання:
2) Чи всі елементи входять у вибірку (сполуку)?
Якщо «так» то обчислюємо через перестановки, якщо «ні» застосовуємо формулу розміщень.
Щоб легше запам'ятались ці правила наведемо наступний рисунок, вивчивши який у Вас не виникатиме труднощів з основними комбінаторними задачами.
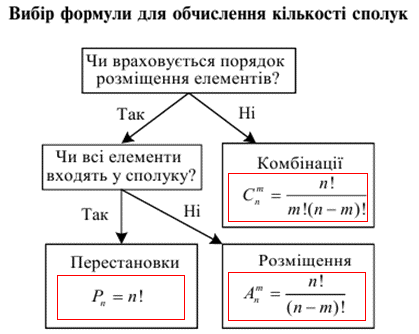
Правила комбінаторного додавання та комбінаторного множення
Правило комбінаторного множення є частковим випадком основного правила комбінаторики: Нехай необхідно виконати послідовно n дій. При цьому першу дію можна виконати k1 способами, другу — k2 способами і так далі до m-ї дії, яку можна виконати km способами.
Тоді всі m дій можна виконати
k1 • k2 • ... • km1 • km2 • ... • km способами.
Скількома способами?
Почнемо з простих прикладів, які Вам допоможуть у вивченні формул.
Приклад 1. Скількома способами можна розставити на полиці 5 різних книжок?
Розв’язання: Спершу обчислимо за допомогою логічних висновків. На перше місце можемо поставити одну з 5 книг, на друге – одну з 4 (оскільки одна вже вибрана на перше місце), на 3 – одну з 3, 4 – одну з 2, і на останнє місце можна поставити ту книгу що залишилася.
Кількість способів розставити книгу рівна добутку кількості варіантів вибрати книгу на кожне місце, тобто
5!=5•4•3•2•1=120 способів.
Тепер розв’яжемо через формули комбінаторики.
Для цього дамо відповідь на 2 запитання описані на початку:
1) Чи враховується порядок розміщення елементів? Так.
2) Чи всі елементи входять до сполуки? Так.
В такому разі обчислюємо перестановки 5 книг
P5=5!= 5•4•3•2•1=120
Відповідь: 120 способів.
Приклад 2. Телефонні номера на початку містять номер операторів 068, 067, 097, 098, а далі йдуть 7 номерів телефону абонента.
Скільки телефонних семизначних номерів можна скласти з цифр від 1 до 9 при умові, що цифри у номері не повторюються?
Розв’язання: Дану задачу можна обчислювати як логічно так і через формули, при великих значеннях цифр або складніших початкових умовах задач логіка вас може підвести, а от формули – ні.
1) Чи враховується порядок розміщення елементів? Так.
2) Чи всі елементи входять до сполуки? Ні, оскільки маємо 9 цифр, а потрібно вибрати 7 із них.
Тоді за наведеною схемою застосовуємо формулу розміщень
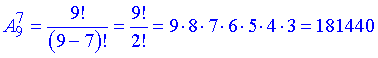
Отримали 181 тисячу 440 різних номерів, в яких цифри від 1 до 9 не повторюються.
Приклад 3. Скількома способами можна вибрати 3 різні фарби із 5 різних фарб?
Розв’язання: Маємо задачу на розміщення (подусайте чому) і алгоритм розрахунків ідентичний до попередньго завдання.
Першою можемо вибрати одну з 5 фарб, другою одну з 4 і третьою одну з 3.
Кількість способів рівна добутку 5•4•3=60 способів.
ІІ спосіб
Перевіряємо умову
1) Чи враховується порядок розміщення елементів? Так.
2) Чи всі елементи входять до сполуки? Ні, тому що маємо 5 різних фарб і всього 3 місця на які їх можна вибрати.
Застосовуємо формулу розміщень з 5 по 3
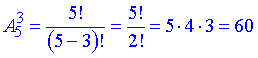
Відповідь: 60.
Приклад 4. Скількома способами можна з 20 чоловік призначити двох чергових з однаковими обов’язками?
Розв’язання: Всі хто хотів робити по аналогії з попередніми завданнями отримають у відповідь 20•19=380, що є неправильним.
А все тому, що маємо підказку «чергові з однаковими обов’язками», тобто Андрій, Василь чи Василь, Андрій є одним і тим самим, однією комбінацією.
А на перше питання «Чи враховується порядок розміщення елементів?» маємо відповідь «Ні».
Тому тут слід використовувати формулу комбінацій з 20 чоловік по 2
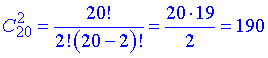
Уважно перегляньте як спрощують факторіали, без розуміння цього Вам доведеться малювати дроби на ширину листка.
Відповідь: є 190 способів вибрати 2 чергових з 20 з однаковими обов’язками.
Приклад 5. Скільки прямих можна побудувати через 10 різних точок?
Розв’язання: З курсу геометрії відомо, що пряму можна побудувати через 2 точки.
Припустимо, що задані точки не лежать на одній прямій, оскільки в протилежному випадку задача буде невизначеною.
Далі нам неважливий порядок розміщення точок на прямій, що веде до застосування формули комбінацій з 10 по 2
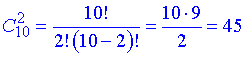
Відповідь: через 10 точок можна побудувати 45 прямих.
Поєднання елементів комбінаторики та комбінаторного множення з додаванням
Далі наведені складніші комбінаторні задачі, які вимагають при обчисленнях застосування однієї з формул комбінаторики + правило додавання або множення, тому уважно перегляньте, як обчислювати коли маємо в умові «І» та «АБО».
Приклад 6. У підрозділі 3 офіцерів та 49 солдат.
Скількома способами можна виділити наряд, який складається із 2 солдат і двох офіцерів?
Розв’язання: Нам неважливо порядок входження офіцерів та солдат в наряд, тому тут застосовуємо комбінації.
Вибрати 2 солдат із 49 можна через комбінації з 49 по 2, офіцерів – з 3 по 2.
Нам потрібно вибрати і солдат і офіцерів, тому застосовуємо формулу комбінаторного множення
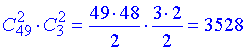
Відповідь: 3528 способами.
Приклад 7. Із 10 троянд і 5 жоржин та 7 ромашок треба скласти букет так, щоб в ньому були по 3 квітки з кожного сорту.
Скількома способами можна скласти букет?
Розв’язання: Порядок входження квітів неважливий, тому через комбінації знаходимо кількість способів вибрати 3 троянди з 10, 3 жоржини з 5 та 3 ромашки з 7.
Далі оскільки маємо букет, то потрібно і ті, і інші квіти. А це правило множення, тому відповіддю буде добуток натупних комбінацій
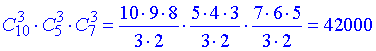
Відповідь: 42000 способів.
Приклад 8. Із шести бігунів і трьох стрибунів треба скласти команду із 4 чоловік, в яку б входив хоча би один стрибун.
Скількома способами це можна зробити?
Розв’язання: Умова хоча б один стрибун при виборі з 3 означає, що або 1 або 2 або 3 стрибуни можна вибирати.
При цьому залишається вибрати ще 3 з шести бігунів для 1 стрибуна,
або 2 з 6 бігунів для 2 стрибунів і
1 з 6 для 3 стрибунів.
Умова «або» означає, що потрібно застосувати комбінаторну формулу додавання.
В підсумку отримаємо суму добутків комбінацій
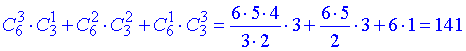
Відповідь: 141 способом.
Складні комбінаторні задачі
Задача 1.26 Скількома способами можна з колоди 36 карт взяти 10 карт так, щоб серед них було точно 8 карт однієї масті?
Розв'язання: В колоді з 36 карт є 4 масті по 9 карт, тому спочатку вибираємо 1 масть з 4 (без повторень, порядок неважливий) через комбінацію з 4 по 1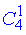
;
з тих 9 карт вибираємо 8 за умовою задачі (без повторень, порядок неважливий) також через комбінацію з 9 по 8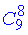 
;
а потім вибираємо інші 2 карти вже з 36-9=27 карт, що залишились (без повторень, порядок неважливий) за аналогічними до попередніх формулами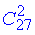 
Досі тричі застосували формулу комбінацій, але це ще не є кінцевою відповіддю.
Далі використовуємо комбінаторне множення, оскільки маємо три «і»
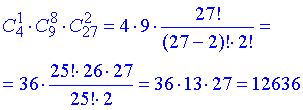
Отже є 12636 способів виконати умови завдання.
Задача 1.27 Скількома способами можна вибрати 6 карт з 52, щоб серед них були карти всіх 4 мастей?
Розв'язання: В колоді з 52 карт є 4 масті по 13 карт, тому:
І) спочатку вибираємо 1 масть з 4 (без повторень, порядок неважливий)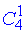 
;
з тих 13 карт вибираємо 3 (без повторень, порядок неважливий)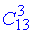 
;
з інших 3-х мастей вибираємо по 1 карті (без повторень, порядок неважливий)
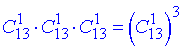, або
ІІ) спочатку вибираємо 2 масті з 4 (без повторень, порядок неважливий)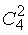 
;
з тих 13 карт однієї масті і 13 карт іншої масті вибираємо 2 карти (без повторень, порядок неважливий)
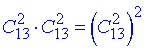
з інших 2-х мастей вибираємо по 1 карті (без повторень, порядок неважливий)
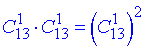
а далі застосовуємо комбінаторне додавання
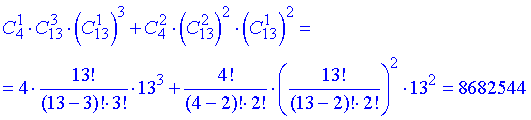
Задача 1.35 Скільки різних «слів» можна утворити перестановкою літер у слові «паралелепіпед»?
Розв'язання: В слові «паралелепіпед» є 13 літер, серед яких 3 – «п», 2 – «а», 1 – «р», 2 – «л», 3 – «е», 1 – «і», 1 – «д».
Маємо перестановку, в якій важливий порядок і елементи повторюються певну кількість разів, тому така кількість рівна перестановкам
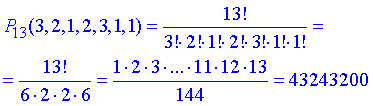
Отримали 43 мільйони 243 тисячі 200 різних наборів перестановок букв.
Задача 1.40 Протягом сесії студенти складають 4 іспити, з яких 2 – з математики.
Скількома способами можна скласти розклад так, щоб іспити з математики не стояли поруч?
Розв'язання: Дана задача дещо двозначна: предмети математики є різні (наприклад алгебра і геометрія), тому їх порядок потрібно враховувати. І тут є два варіанти:
іспити з математики мають йти за порядком або їх можна переставляти.
Якщо можна переставляти, тоді справедливі наступні міркування: з 4-х іспитів предмет з математики може стояти або першим, або останнім.
Якщо іспит з математики стоїть першим, то наступний не буде з математики, далі залишається вибрати ще 2 предмета з 3-х (без повторень, порядок важливий):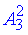 
, результат будемо множити на 2, оскільки врахуємо і зворотній порядок (від 4-го до 1-го іспиту), тому отримаємо 12 способів.
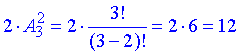способів.
Якщо іспити з математики не можна міняти порядком то різних способів вдвоє менше – 6.
Їх не багато, тому можемо всіх виписати, позначивши цифрами номера екзаменів з математики, а латинськими буквами два інші екзамени.
1а3b
1b3a
a2b4
b2a4
1ab4
1ba4
Це і є шукані 6 способів, якщо якщо екзамени з математики не можна переставляти місцями.
Завдання (номера) в попередніх задачах взяті з навчального посібника:
Бордуляк М. Т. Теореми і задачі теорії ймовірності: навч. посібн. / М. Т. Бордуляк, О. Б. Скасків, О. М. Сумик, І. Е. Чижиков – Львів: Видавець І. Е. Чижиков, 2013. – 175 с. – (Серія «Математичний практикум»).
