Нижче наведена 3 частина відповідей з індивідуальних завдань з теорії ймовірностей. З прикладів Ви навчитеся визначати числові характеристики статистичного розподілу вибірки, знаходити рівняння регресії між двома ознаками, розв'язувати приклади на перевірку гіпотези А за наявної гіпотези В. Перевірка гіпотез дається легко не всім студентам, тому уважно розбирайте відповіді та використовуйте формули ймовірності у навчанні.
Варіант 13 . Індивідуальне завдання 3.
Завдання 1. У таблиці наведено емпіричні частоти 
та теоретичні частоти 
, обчислені, виходячи з гіпотези 
про нормальний розподіл генеральної сукупності. Для рівня значущості 
перевірити гіпотезу 
про нормальний розподіл генеральної сукупності.
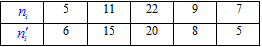
Розв'язання:
Обчислимо емпіричне значення критерію Пірсона (
)
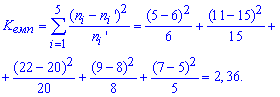
За таблицею критичних точок розподілу "хі-квадрат" 
для рівня значущості 
і кількості ступенів вільності 
(r=2 для нормального розподілу) знаходимо:
Оскільки емпіричне значення менше критичного
, то гіпотезу H0 приймаємо.
Завдання 2. Із нормально розподіленої генеральної сукупності з відомим середнім квадратичним відхиленням 
=2,0 одержано вибірку обсягом n=64 і за нею знайдено вибіркове середнє 
=94,4 Для рівня значущості 
=0,01 перевірити гіпотезу 
за наявності альтернативної гіпотези 
.
Розв'язання:
Обчислимо емпіричне значення критерію:
Для альтернативної гіпотези 
знаходимо 
за таблицею значень функції Лапласа, використовуючи формули
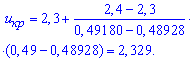
Оскільки емпіричне значення U менше критичного u
то гіпотезу H0 відхиляємо і приймаємо гіпотезу H1 .
Завдання 3. За вибіркою обсягу n=25 з нормально розподіленої генеральної сукупності знайдено вибіркове середнє 
=94,4 і підправлене середнє квадратичне відхилення s=2,0. Для рівня значущості 
=0,05 перевірити гіпотезу 
за наявності альтернативної гіпотези 
.
Розв'язання:
Обчислимо емпіричне значення критерію:
Знаходимо за таблицею критичних точок розподілу Ст'юдента за заданим рівнем значущості 
(для двосторонньої критичної області) і кількістю ступенів вільності k=25-1=24 критичну точку 
.
Оскільки умова виконується 
, то гіпотезу H0 приймаємо.
Завдання 4. За вибіркою обсягу n=17 з нормально розподіленої генеральної сукупності знайдено підправлену дисперсію 
=4,8. Для рівня значущості 
=0,02 перевірити гіпотезу 
за наявності альтернативної гіпотези 
Розв'язання:
Обчислимо емпіричне значення критерію:
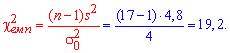
За допомогою таблиці критичних точок розподілу "хі -квадрат" 
визначаємо "ліву" критичну точку
і "праву" критичну точку
Оскільки емпіричне значення критерію належить інтервалу критичних точок розподілу
, то гіпотезу H1 приймаємо.
Завдання 5. За вибіркою обсягу n=19 з нормально розподіленої генеральної сукупності знайдено підправлену дисперсію 
=4,3. Для рівня значущості 
=0,01 перевірити гіпотезу 
за наявності альтернативної гіпотези 
Розв'язання:
Обчислимо емпіричне значення критерію:
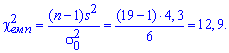
За допомогою таблиці критичних точок розподілу "хі -квадрат"
визначаємо
Оскільки 
, то гіпотезу H0 приймаємо.
На цьому одне з індивідуальних завдань розв'язано та обґрунтовано. Формул з ймовірності Ви вивчили чимало, як перевірити гіпотези знаєте з наведених прикладів. Більше готових контрольних з теорії ймовірностей Ви знайдете в категорії "Контрольні з ймовірності". Також завжди можете замовити контрольну з ймовірності у нас, як Ви переконалися такі завдання нам під силу!
