Як знайти інтервал довіри?

Продовжуємо розгляд індивідуального завдання з теорії ймовірностей. Наведена схема обчислень допоможе знайти інтервал довіри. Формули для інтервалу не складні, в цьому Ви скоро переконаєтесь. Наведені завдання задавали економістам ЛНУ ім. І.Франка. ВУЗи інших міст України мають подібну програму навчання, тому для себе корисного матеріалу знайде кожен студент.

Алгоритм знаходження інтервалу довіри

Завдання 2. Знайти інтервал довіри для оцінки з надійністю γ невідомого математичного сподівання а нормально розподіленої ознаки Х генеральної сукупності:

а) якщо γ=0,92, генеральне середнє квадратичне відхилення σ=4,0, вибіркове середнє =15,0, а обсяг вибірки n=16;

б) якщо γ=0,99, підправлене середнє квадратичне відхилення s=4,0, вибіркове середнє =20,0, а обсяг вибірки n=16.

Розв'язання: а) З рівняння за допомогою функції Лапласа методом інтерполяції знаходимо

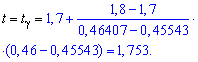
Межі інтервалу довіри шукаємо за формулами:

Отже, отримали інтервал довіри з надійністю 0,92.

б) Оскільки n=16<30 і середнє квадратичне відхилення невідоме, то для знаходження меж інтервалу довіри використаємо формулу

де значенняшукаємо за допомогою таблиць (розподіл Ст'юдента):

Інтервал довіри рівний з надійністю =0,99.

Завдання 3. Знайти інтервал довіри для оцінки з надійністю γ=0,99 невідомого середнього квадратичного відхилення σ нормально розподіленої ознаки Х генеральної сукупності, якщо обсяг вибірки n=35, а підправлене середнє квадратичне відхилення s=13,3.
Розв'язання: Задача зводиться до відшукання інтервалу довіри , який покриває з заданою надійністю 0,99.
За таблицею знаходимо q

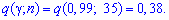
Шуканий інтервал довіри лежить в межах або
.

Варіант 1

Завдання 2. Знайти інтервал довіри для оцінки з надійністю γ невідомого математичного сподівання а нормально розподіленої ознаки Х генеральної сукупності:

а) якщо 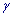=0,9, генеральне середнє квадратичне відхилення s=3,0, вибіркове середнє =7,0, а об'єм вибірки n=9;
б) якщо 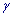=0,95, підправлене середнє квадратичне відхилення s=3,0, вибіркове середнє =15,0, а обсяг вибірки n=9.

Розв'язання: а) З рівняння за допомогою функції Лапласа методом інтерполяції знаходимо t

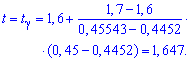
Інтерполяцію використовуємо для уточнення t, коли в таблиці значень функції Лапласа Ф(t) міститься між двома сусідніми.
Межі інтервалу довіри шукаємо за формулами:

Остаточно отримуємо такий інтервал довіри з надійністю 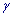=0,9 2.

б) Оскільки n=9<30 і середнє квадратичне відхилення невідоме, то для знаходження меж інтервалу довіри використаємо формули
,
де значення t шукаємо за допомогою таблиць (розподілу Ст'юдента):

Формули як бачите не складні і знайти інтервал довіри може не тільки студент, я й школяр.
Отже ми знайшли інтервал довіри з надійністю =0,95.

Завдання 3.Знайти інтервал довіри для оцінки з надійністю=0,95 невідомого середнього квадратичного відхилення σ нормально розподіленої ознаки Х генеральної сукупності, якщо обсяг вибірки n=17, а підправлене середнє квадратичне відхилення σ=11,2.
Розв'язання: Задача зводиться до відшукання інтервалу довіри , при заданому середньому квадратичному відхиленні з заданою надійністю =0,95.
За таблицею знаходимо значення функції q

Далі за формулами обчислюємо інтервал довіри

Після обчислень він лежатиме в межах

На цьому завдання розв'язано.

Варіант-12

Завдання 2. Знайти інтервал довіри для оцінки з надійністю невідомого математичного сподівання та нормально розподіленої ознаки Х генеральної сукупності:
а) якщо =0,94, генеральне середнє квадратичне відхилення =5,0, вибіркове середнє =18,0, а обсяг вибірки n=25;
б) якщо =0,999, підправлене середнє квадратичне відхилення s=5,0, вибіркове середнє =26,0, а обсяг вибірки n=25.
Розв'язання: а) З рівняння за допомогою функції Лапласа методом інтерполяції знаходимо t

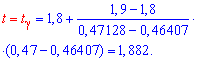
Межі інтервалу довіри шукаємо за формулами:

Отже, інтервал приймає множину значень з надійністю .

б) Оскільки n=25<30 і середнє квадратичне відхилення невідоме, то для знаходження меж інтервалу довіри використаємо формули

де значення t - шукаємо за допомогою таблиць (розподілe Ст'юдента):

Далі знаходимо межі інтервалу довіри.

Отримали інтервал довіри з надійністю 0,999.

Завдання 3. Знайти інтервал довіри для оцінки з надійністю =0,999 невідомого середнього квадратичного відхилення σ нормально розподіленої ознаки Х генеральної сукупності, якщо обсяг вибірки n=45, а підправлене середнє квадратичне відхилення s=15,1.
Розв'язання: Задача зводиться до відшукання інтервалу довіри за формулою

такого, що покриває з заданою надійністю .
За таблицею знаходимо значення функції q

Після цього виконуємо обчислення меж інтервалу довіри

Як бачите, обчислення не складні, тож вивчайте формли та застосовуйте їх на контрольних і тестах з теорії ймовірностей.