Формули перевірки гіпотез на нормальний розподіл

З третього індивідуального завдання Ви вивчите методику перевірки гіпотез на нормальний розподіл генеральної сукупності. Таких варіантів всього 5 і всі вони нижче будуть описані.

Варіант - 8

Завдання 1. У таблиці наведено емпіричні частоти n_i та теоретичні частоти n'_i, обчислені, виходячи з гіпотези H₀ про нормальний розподіл генеральної сукупності. Для рівня значущості alpha= 0,01 перевірити гіпотезу H₀ про нормальний розподіл генеральної сукупності.

Розв'язання: Знайдемо емпіричне значення критерію Пірсона (m=5)

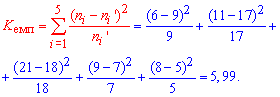
За таблицею критичних точок розподілу 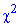для рівня значущості alpha= 0,01 і кількості ступенів вільності k=m-r-1=5-2-1=2 (r=2 для нормального розподілу) знаходимо:

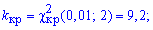
Отже K_emp<k_kr, тому гіпотезу H₀ приймаємо.

Завдання 2. Із нормально розподіленої генеральної сукупності з відомим середнім квадратичним відхиленням 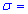0,5 одержано вибірку обсягом n=64 і за нею знайдено вибіркове середнє 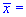77,88. Для рівня значущості 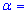0,05 перевірити гіпотезу H₀: a=a₀=78 за наявності альтернативної гіпотези .
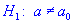Розв'язання: Обчислимо емпіричне значення критерію:

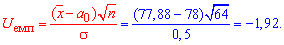
Для альтернативної гіпотези H₁: 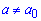знаходимо u_кр за таблицею значень функції Лапласа, використовуючи формули
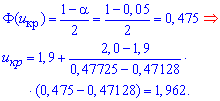
функція Лапласа
Оскільки 1,92=|U_emp|<u_kr=1,962, то гіпотезу H₀ приймаємо.

Завдання 3. За вибіркою обсягу n=16 з нормально розподіленої генеральної сукупності знайдено вибіркове середнє 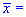89,7 і підправлене середнє квадратичне відхилення s=1,0. Для рівня значущості 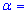0,025 перевірити гіпотезу H₀: a=a₀=89 за наявності альтернативної гіпотези H₁: a>a₀.

Розв'язання: Встановимо емпіричне значення критерію "хі-квадрат":

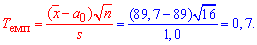
Знаходимо за таблицею критичних точок розподілу Ст'юдента за заданим рівнем значущості 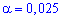(для односторонньої критичної області) і кількістю ступенів вільності k=16-1=15 критичну точку
.
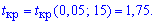Оскількиф емпіричне значення менше критичного 0,7=|T_emp|<t_kr=1,75, то гіпотезу H₀ приймаємо.

Завдання 4. За вибіркою обсягу n=21 з нормально розподіленої генеральної сукупності знайдено підправлену дисперсію 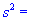13,3 Для рівня значущості 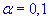перевірити гіпотезу 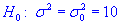за наявності альтернативної гіпотези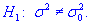

Розв'язання: Визначимо емпіричне значення критерію:

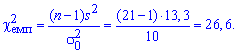
За допомогою таблиці критичних точок розподілу 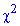визначаємо «ліву» критичну точку

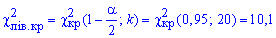
і «праву» критичну точку

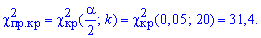
Оскільки маємо 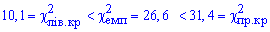, то гіпотезу H₁ приймаємо.

Завдання 5. За вибіркою обсягу n=15 з нормально розподіленої генеральної сукупності знайдено підправлену дисперсію 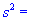6,3. Для рівня значущості 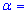0,025 перевірити гіпотезу 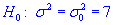за наявності альтернативної гіпотези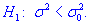
Розв'язання: Знаходимо емпіричне значення критерію:

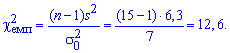
За допомогою таблиці критичних точок розподілу 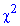визначаємо

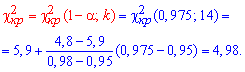
Оскільки умова виконується 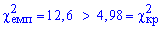, то гіпотезу H₀ приймаємо.
Якщо на контрольній чи тестах виконаєте обчислення та обґрунтовання подібно до наведеного, то з ймовірності у викладачів до Вас точно не буде претензій. В усіх решта випадках звертайтеся за допомогою до Нас!