Индивидуальное задание 1
Вариант 11
Задача 1. Построить статистическое распределение выборки, записать эмпирическую функцию распределения и вычислить такие числовые характеристики:
- выборочное среднее;
- выборочную дисперсию;;
- подправленную дисперсию;
- выборочное среднее квадратичное отклонение;
- подправленное среднее квадратичное отклонение;
- размах выборки;
- медиану;
- моду;
- квантильное отклонение;
- коэффициент вариации;
- коэффициент асимметрии;
- эксцесс для выборки:
Выборка задана рядом 11, 9, 8, 7, 8, 11, 10, 9, 12, 7, 6, 11, 8, 7, 10, 9, 11, 8, 13, 8.
Решение:
Запишем выборку в виде вариационного ряда (в порядке возрастания):
6; 7; 7; 7; 8; 8; 8; 8; 8; 9; 9; 9; 10; 10; 11; 11; 11; 11; 12; 13.
Далее записываем статистическое распределение выборки в виде дискретного статистического распределения частот:
![]()
Эмпирическую функцию распределения определим по формуле
![]()
Здесь nx – количество элементов выборки которые меньше х. Используя таблицу и учитывая что объем выборки равен n = 20, запишем эмпирическую функцию распределения:

Далее вычислим числовые характеристики статистического распределения выборки.
Выборочное среднее вычисляем по формуле
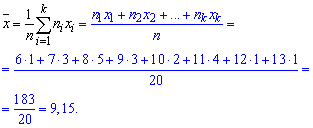
Выборочную дисперсию находим по формуле
![]()
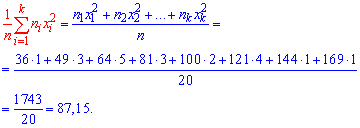
Выборочное среднее, что фигурирует в формуле дисперсии в квадрате найдено выше. Остается все подставить в формулу
![]()
Подправленную дисперсию вычисляем согласно формулы
![]()
Выборочное среднее квадратичное отклонение вычисляем по формуле
![]()
Подправленное среднее квадратичное отклонение вычисляем как корень из подправленной дисперсии
![]()
Размах выборки вычисляем как разность между наибольшим и наименьшим значениями вариант, то есть:
![]()
Медиану находим по 2 формулам:
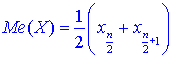 если число n - четное;
если число n - четное;
![]() если число n - нечетное.
если число n - нечетное.
Здесь берем индексы в xi согласно нумерации варианта в вариационном ряду.
В нашем случае n = 20, поэтому
![]()
Мода – это варианта которая в вариационном ряду случается чаще всего, то есть
![]()
Квантильное отклонение находят по формуле
![]()
где ![]() – первый квантиль,
– первый квантиль, ![]() – третий квантиль.
– третий квантиль.
Квантили получаем при разбивке вариационного ряда на 4 равные части.
Для заданного статистического распределения квантильное отклонения примет значение
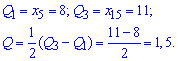
Коэффициент вариации равный процентному отношению подправленного среднего квадратичного к выборочному среднему
![]()
Коэффициент асимметрии находим по формуле
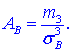
Здесь 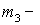 центральный эмпирический момент 3-го порядка,
центральный эмпирический момент 3-го порядка,
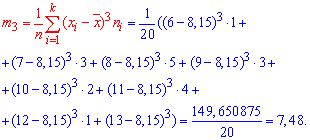
Подставляем в формулу коэффициента асимметрии
![]()
Эксцессом ![]() статистического распределения выборки называется число, которое вычисляют по формуле:
статистического распределения выборки называется число, которое вычисляют по формуле:
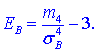
Здесь m4 центральный эмпирический момент 4-го порядка. Находим момент
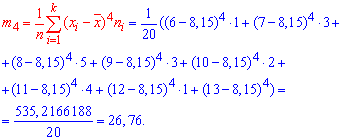
а далее эксцесс![]()
Теперь Вы имеете все необходимые формулы чтобы найти числовые характеристики статистического распределения. Как найти моду, медиану и дисперсию должен знать каждый студент, который изучает теорию вероятностей.
Готовые решения по теории вероятностей
- Следующая статья - Построение уравнения прямой регрессии Y на X
Индивидуальное задание 1
Вариант 11
Задача 1. Связь между признаками Х и Y генеральной совокупности задается таблицей:

Записать выборочное уравнение прямой регрессии Y на X.
Решение: Вычисляем средние арифметические значения признаков Х та Y
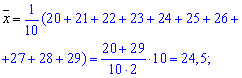
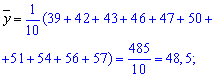
Находим величины которые фигурируют в уравнении регрессии - alpha, beta
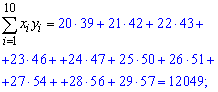
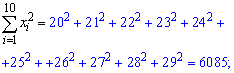
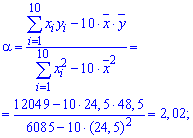
После вычислений выборочное уравнение регрессии Y на X записываем по формуле
y=2,02*x-0,99.
Чтобы подтвердить правильность предположения о линейности связи между признаками Х и Y находим выборочный коэффициент корреляции по формуле:
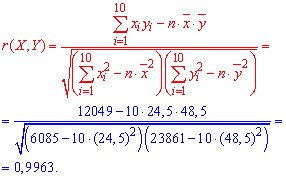
Так как выборочный коэффициент корреляции r(X,Y) является достаточно близким к единице, то предположение о линейной зависимости между X и Y - правильное. Кроме этого коэффициент корреляции положительный r>0, поэтому случайные величины X и Y увеличиваются одновременно.
Вариант 1
Задача 1. Связь между признаками Х и Y генеральной совокупности задается таблицей:
Записать выборочное уравнение прямой регрессии Y на X.
Решение: Находим величины которые необходимы для вычисления коэффициентов уравнения регрессии
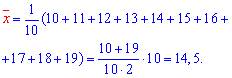
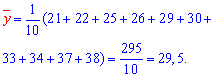
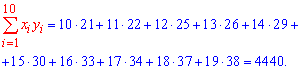
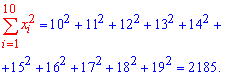
Вычисляем alpha, beta
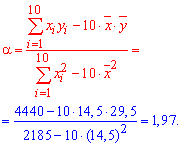
![]()
и составляем уравнение регрессии Y на X
y=19,7*x+0,935.
Xтобы убедиться что предположение о линейной свя связи между Х и Y является правильным, находим выборочный коэффициент корреляции по формуле:
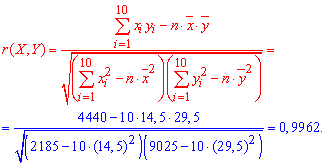
Поскольку выборочный коэффициент корреляции ![]() =0,9962 достаточно близок к единице, то предположение о линейной связи между X и Y -правильное.
=0,9962 достаточно близок к единице, то предположение о линейной связи между X и Y -правильное.
К тому же коэффициент корреляции положительный (r>0), поэтому и связь между X и Y является положительной, то есть эти случайные величины увеличиваются одновременно.
Вариант-12
Задача 1. Связь между признаками Х и Y генеральной совокупности задается таблицей:

Записать выборочное уравнение прямой регрессии Y на X.
Решение: Вычисляем средние арифметические значения каждой из выборок, а также остальные составляющие для построения уравнения регрессии Y на X:
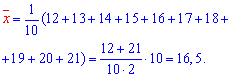
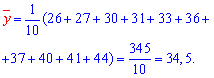
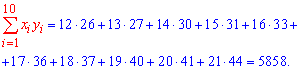
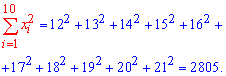
Находим коэффициенты alpa, beta по формулам
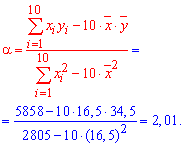
![]()
Подставляем коэффициенты в уравнение прямой регрессии y=2,01*x+1,335.
Находим точечную оценку для коэффициента корреляции по формуле:
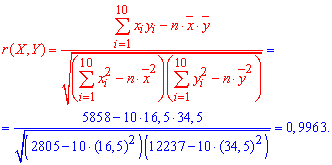
Поскольку выборочный коэффициент корреляции ![]() достаточно близок к единице то предположение о линейной зависимости между X и Y - правильное.
достаточно близок к единице то предположение о линейной зависимости между X и Y - правильное.
Также r>0, поэтому связь между X и Y положительная и эти случайные величины увеличиваются одновременно.
Теперь Вы знаете, как составить уравнение прямой регрессии Y на X .
Готовые решения по теории вероятностей
- Предыдущая статья - Формулы числовых характеристик статистического распределения
- Следующая статья - Как найти доверительный интервал?
Индивидуальное задание 1
Вариант 11
Задача 2. Найти доверительный интервал для оценки с надежностью γ неизвестного математического ожидания а нормально распределенного признака Х генеральной совокупности:
а) если γ=0,92, генеральная среднее квадратичное отклонение σ=4,0, выборочное среднее  =15,0, а объем выборки n=16;
=15,0, а объем выборки n=16;
б) если γ=0,99, подправленное среднее квадратичное отклонение s=4,0, выборочное среднее ![]() =20,0, а объем выборки n=16.
=20,0, а объем выборки n=16.
Решение: а) Из уравнения ![]()
 с помощью функции Лапласа методом интерполяции находим t
с помощью функции Лапласа методом интерполяции находим t
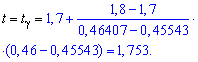
Границы интервала доверия ищем по формулам:
![]()
![]()
После вычислений получим интервал доверия ![]() с надежностью
с надежностью ![]() 0,92.
0,92.
2, б) Поскольку n=16<30 и среднее квадратичное отклонение  неизвестно, то для нахождения границ интервала доверия используем формулу
неизвестно, то для нахождения границ интервала доверия используем формулу
![]()
где ![]() ищем с помощью таблиц (распределение Стьюдента):
ищем с помощью таблиц (распределение Стьюдента):
![]()
![]()
![]()
Таким образом доверительный интервал равный ![]() с надежностью
с надежностью ![]() =0,99.
=0,99.
Задача 3. Найти интервал доверия для оценки с надежностью γ=0,99 неизвестного среднего квадратичного отклонения σ нормально распределенного признака Х генеральной совокупности, если объем выборки n = 35, а подправленное среднее квадратичное отклонение s=13,3.
Решение: Задача сводится к отысканию интервала доверия ![]() который покрывает
который покрывает  с заданной надежностью
с заданной надежностью ![]() 0,99.
0,99.
По таблице находим q
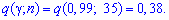
Искомый доверительный интервал лежит в пределах ![]() или
или
![]() .
.
Вариант 1
Задача 2. Найти доверительный интервал для оценки с надежностью γ неизвестного математического ожидания а нормально распределенного признака Х генеральной совокупности:
- а) если
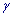 =0,9, генеральная среднее квадратичное отклонение s=3,0, выборочное среднее
=0,9, генеральная среднее квадратичное отклонение s=3,0, выборочное среднее  =7,0, а объем выборки n=9;
=7,0, а объем выборки n=9; - б) если
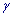 =0,95, подправленное среднее квадратичное отклонение s=3,0, выборочное среднее
=0,95, подправленное среднее квадратичное отклонение s=3,0, выборочное среднее  =15,0, а объем выборки n=9.
=15,0, а объем выборки n=9.
Решение: а) Из уравнения на функцию Лапласа ![]() с помощью таблиц методом интерполяции находим t
с помощью таблиц методом интерполяции находим t
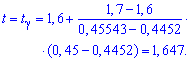
Интерполяцию используем для уточнения t (когда в таблице значений функции Лапласа Ф(t) находится между двумя соседними).
Границы интервала доверия ищем по формулам:
![]()
![]()
Окончательно получаем такой интервал доверия ![]() с надежностью
с надежностью 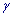 =0,9 2.
=0,9 2.
б) Поскольку n=9<30 и среднее квадратичное отклонение ![]() неизвестно, то для нахождения границ интервала доверия используем формулы
неизвестно, то для нахождения границ интервала доверия используем формулы
![]() ,
,
где значение t ![]() ищем с помощью таблиц распределения Стьюдента:
ищем с помощью таблиц распределения Стьюдента:
![]()
![]()
![]()
Формулы как видите не сложные и найти интервал доверия может как студент, так и школьник.
Мы нашли интервал доверия![]() с надежностью
с надежностью ![]() =0,95.
=0,95.
Задача 3. Найти интервал доверия для оценки с надежностью ![]() =0,95 неизвестного среднего квадратичного отклонения σ нормально распределенного признака Х генеральной совокупности, если объем выборки n = 17, а подправленное среднее квадратичное отклонение σ=11,2.
=0,95 неизвестного среднего квадратичного отклонения σ нормально распределенного признака Х генеральной совокупности, если объем выборки n = 17, а подправленное среднее квадратичное отклонение σ=11,2.
Решение: Формулы для интервала доверия ![]() достаточно просты.
достаточно просты.
По таблице находим значение функции q
![]()
Далее по формулам вычисляем интервал доверия
![]()
После вычислений он будет лежать в пределах
![]()
Вариант-12
Задача 2. Найти доверительный интервал для оценки с надежностью ![]() неизвестного математического ожидания и нормально распределенного признака Х генеральной совокупности:
неизвестного математического ожидания и нормально распределенного признака Х генеральной совокупности:
а) если ![]() =0,94, генеральная среднее квадратичное отклонение
=0,94, генеральная среднее квадратичное отклонение ![]() =5,0, выборочное среднее
=5,0, выборочное среднее ![]() =18,0, а объем выборки n=25;
=18,0, а объем выборки n=25;
б) если ![]() =0,999, подправленное среднее квадратичное отклонениеs=5,0, выборочное среднее
=0,999, подправленное среднее квадратичное отклонениеs=5,0, выборочное среднее ![]() =26,0, а объем выборки n=25.
=26,0, а объем выборки n=25.
Решение: а) Из уравнения на функцию Лапласа ![]() с помощью таблиц распределения методом интерполяции находим t
с помощью таблиц распределения методом интерполяции находим t
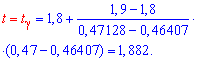
Крайние точки доверительного интервала ищем по формуле:
![]()
![]()
Итак, интервал принимает множество значений ![]() с надежностью 0,94.
с надежностью 0,94.
2, б) Поскольку n=25<30 и среднее квадратичное отклонение ![]() неизвестно, то для нахождения границ интервала доверия используем формулы
неизвестно, то для нахождения границ интервала доверия используем формулы
![]()
где значение t - ![]() ищем с помощью таблиц распределения Стьюдента:
ищем с помощью таблиц распределения Стьюдента:
![]()
Далее находим границы интервала доверия.
![]()
![]()
Таким образом нашли доверительный интервал ![]() с надежностью
с надежностью ![]() 0,999.
0,999.
Задача 3. Найти доверительный интервал для оценки с надежностью ![]() =0,999 неизвестного среднего квадратичного отклонения σ нормально распределенного признака Х генеральной совокупности, если объем выборки n = 45, а подправленное среднее квадратичное отклонение s=15,1.
=0,999 неизвестного среднего квадратичного отклонения σ нормально распределенного признака Х генеральной совокупности, если объем выборки n = 45, а подправленное среднее квадратичное отклонение s=15,1.
Решение: Найдем интервал доверия по формуле
![]()
По таблице находим значение функции q
![]()
После этого выполняем вычисления границ интервала доверия
![]()
![]()
Как видите формулы для вычисления доверительного интервала не сложные, поэтому с легкостью применяйте их на контрольных и тестах по теории вероятностей.
Готовые решения по теории вероятностей
- Предыдущая статья - Построение уравнения прямой регрессии Y на X
- Следующая статья - Проверка гипотез о нормальном распределении генеральной совокупности
Задания 11 и 12 вариантов помогут в первую очередь экономистам ВУЗов Украины и каждый студент для себя сможет почерпнуть много полезного материала .
Индивидуальное задание 3
Вариант-11
Задача 1. В таблице приведены эмпирические частоты ni и теоретические частоты
Решение: Сначала вычисляем эмпирическое значение критерия Пирсона (m=5)
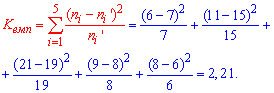
Далее по таблице критических точек распределения хи-квадрат ![]() для уровня значимости
для уровня значимости ![]() 0,05 и числа степеней свободы k=m-r-1=5-2-1=2 (r=2 для нормального распределения) находим (методом интерполяции) критическое значение:
0,05 и числа степеней свободы k=m-r-1=5-2-1=2 (r=2 для нормального распределения) находим (методом интерполяции) критическое значение:
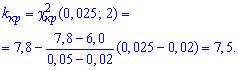
Условие выполняется ![]() , поэтому гипотезу H0 принимаем.
, поэтому гипотезу H0 принимаем.
Задача 2. Для нормально распределенной генеральной совокупности с известным средним отклонениям ![]() 4,0 получено выборку объемом n=64 и за ней найдено выборочное среднее
4,0 получено выборку объемом n=64 и за ней найдено выборочное среднее ![]() 89,7. Для уровня значимости
89,7. Для уровня значимости![]() 0,05 проверить гипотезу H0: a=a0=89 при наличии альтернативной гипотезы H1: a>a0.
0,05 проверить гипотезу H0: a=a0=89 при наличии альтернативной гипотезы H1: a>a0.
Решение: Вычислим эмпирическое значение критерия:
![]()
Для альтернативной гипотезы H1: a>a0 находим критическое значение uкр по таблице значений функции Лапласа, используя формулы
![]()
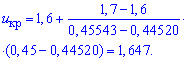
Поскольку условие выполняется ![]() то гипотезу H0 принимаем.
то гипотезу H0 принимаем.
Задача 3. По выборке объемом n=16 для нормально распределенной генеральной совокупности найдено выборочное среднее 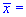 89,7 и подправленное среднее квадратическое отклонение s=2,0. Для уровня значимости
89,7 и подправленное среднее квадратическое отклонение s=2,0. Для уровня значимости 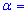 0,05 проверить гипотезу a=a0=89 при наличии альтернативной гипотезы H1: a<>a0.
0,05 проверить гипотезу a=a0=89 при наличии альтернативной гипотезы H1: a<>a0.
Решение: Вам следует помнить что подправленное и среднее квадратическое отклонение незначительно отличаются на практике. Поэтому формулы которые рассматривали в предыдущем задании актуальны и здесь. Только меняется обозначение с сигма на s. Переходим к нахождению величин, сначала эмпирическое значение критерия:
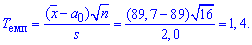
Далее с таблицы критических точек распределения Стьюдента по заданному уровню значимости 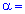 0,05 (для двусторонней критической области) и количества степеней свободы k=16-1=15 находим критическую точку
0,05 (для двусторонней критической области) и количества степеней свободы k=16-1=15 находим критическую точку
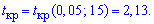
Проверяем условие 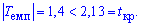 и принимаем гипотезу H0 .
и принимаем гипотезу H0 .
Как видите вычисления не сложные и по приведенной схеме сможете самостоятельно сделать индивидуальное задания по теории вероятности или контрольную роботу.
Задача 4. Для выборки объемом n=15 нормально распределенной генеральной совокупности найдено подправленную дисперсию 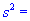 4,2. Для уровня значимости
4,2. Для уровня значимости 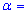 0,1 проверить гипотезу
0,1 проверить гипотезу 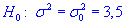 при наличии альтернативной гипотезы
при наличии альтернативной гипотезы 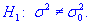
Решение:
По формуле находим эмпирическое значение критерия Пирсона:
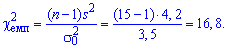
С помощью таблицы критических точек распределения "хи -квадрат" 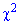 определяем критические точки слева и справа
определяем критические точки слева и справа
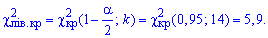
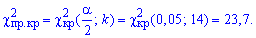
Поскольку эмпирическое значение принадлежит интервалу
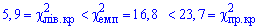
то гипотезу H1 принимаем.
Задача 5. По выборке объемом n=21 нормально распределенной генеральной совокупности найдено подправленную дисперсию 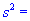 3,4. Для уровня значимости
3,4. Для уровня значимости 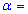 0,025 проверить гипотезу
0,025 проверить гипотезу 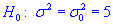 при наличии альтернативной гипотезы
при наличии альтернативной гипотезы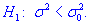
Решение: Определяем эмпирическое значение критерия:
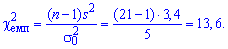
Далее с таблицы критических точек распределения 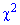 находим значение
находим значение
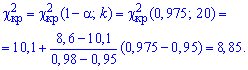
Сравнением величины 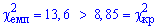 и делаем вывод о принятии гипотезы H0.
и делаем вывод о принятии гипотезы H0.
Индивидуальное задание 3
Вариант 12
Задача 1. В таблице приведены эмпирические частоты ![]() и теоретические частоты
и теоретические частоты ![]() , рассчитанные исходя из гипотезы H0 о нормальном распределении генеральной совокупности. Для уровня значимости
, рассчитанные исходя из гипотезы H0 о нормальном распределении генеральной совокупности. Для уровня значимости ![]() 0,05 проверить гипотезу H0 о нормальном распределении генеральной совокупности.
0,05 проверить гипотезу H0 о нормальном распределении генеральной совокупности.
![]()
Решение: Схема расчетов достаточно проста и сводится к нахождению и сравнения двух величин.
Сначала вычисляем эмпирическое значение критерия Пирсона (для m = 5) по формуле
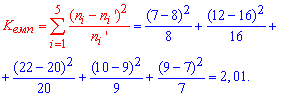
Далее по таблице критических точек распределения "хи-квадрат" ![]() для уровня значимости
для уровня значимости ![]() 0,05 и числа степеней свободы 2
0,05 и числа степеней свободы 2
![]()
(r=2 для нормального распределения) находим критическое значение:
![]()
Сравнением емпирическое и критическое значения для гипотезы![]() и принимаем гипотезу H0.
и принимаем гипотезу H0.
Задача 2. Для нормально распределенной генеральной совокупности с известным средним отклонениям![]() 1,75 получено выборку объемом n=49 и за ней найдено выборочное среднее
1,75 получено выборку объемом n=49 и за ней найдено выборочное среднее 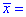 84,7. Для уровня значимости
84,7. Для уровня значимости ![]() 0,1 проверить гипотезу H0: a=a[0]=85 при наличии альтернативной гипотезы H1: a < a[0].
0,1 проверить гипотезу H0: a=a[0]=85 при наличии альтернативной гипотезы H1: a < a[0].
Решение:
Вичысляем эмпирическое значение критерия Пирсона:
![]()
Для альтернативной гипотезы H1: a < a[0] находим критическое значение ![]() по таблице значений функции Лапласа. Для уточнения uкр используем формулу интенрполяции
по таблице значений функции Лапласа. Для уточнения uкр используем формулу интенрполяции
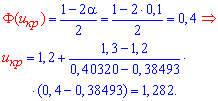
Поскольку выполняется условие ![]() то принимаем гипотезу H0.
то принимаем гипотезу H0.
Задача 3. По выборке объемом n=9 нормально распределенной генеральной совокупности найдено выборочное среднее ![]() 84,7 и подправленное среднее квадратическое отклонение s=0,5. Для уровня значимости
84,7 и подправленное среднее квадратическое отклонение s=0,5. Для уровня значимости ![]() 0,01 проверить гипотезу
0,01 проверить гипотезу ![]() при наличии альтернативной гипотезы.
при наличии альтернативной гипотезы. ![]()
Решение: Согласно методике вычислим эмпирическое значение критерия:
![]()
Далее по таблице критических точек распределения Стьюдента находим для заданного уровня значимости ![]() 0,01 (для двусторонней критической области) и количеством степеней свободы k=9-1=8 критическую точку
0,01 (для двусторонней критической области) и количеством степеней свободы k=9-1=8 критическую точку
![]() .
.
Сравнением емпирическое и критичное значение ![]() и приходим к выводу, что гипотезу H0 принимаем.
и приходим к выводу, что гипотезу H0 принимаем.
Задача 4. По выборке объемом n=29 нормально распределенной генеральной совокупности найдено подправленную дисперсию ![]() 7,7. Для уровня значимости
7,7. Для уровня значимости ![]() 0,05 проверить гипотезу H0 :
0,05 проверить гипотезу H0 :![]() при наличии альтернативной гипотезы H1:
при наличии альтернативной гипотезы H1:![]()
Решение: Вычислим эмпирическое значение критерия по формуле
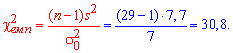
С помощью таблицы критических точек распределения "хи-квадрат" ![]() определяем «левую» критическую точку
определяем «левую» критическую точку
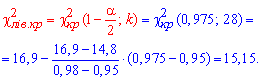
и «правую» критическую точку
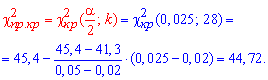
Так как эмпирическое значение принадлежит найденному интервалу
![]()
то гипотезу H1 принимаем..
Задача 5. По выборке объемом n=25 нормально распределенной генеральной совокупности найдено подправленную дисперсию ![]() 6,2. Для уровня значимости
6,2. Для уровня значимости ![]() 0,05 проверить гипотезу H0:
0,05 проверить гипотезу H0:![]() при наличии альтернативной гипотезы H1
при наличии альтернативной гипотезы H1 ![]()
Решение: Находим эмпирическое значение критерия "хи -квадрат":
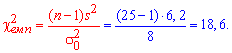
Далее с помощью таблицы критических точек распределения ![]() определяем
определяем
![]()
Поскольку условие ![]() выполняется, то гипотезу H0 принимаем.
выполняется, то гипотезу H0 принимаем.
Теперь Вы знаете, как проверить гипотезу о нормальном распределении генеральной совокупности.
Готовые решения по теории вероятностей
]]> в соответствие ставится число
в соответствие ставится число 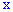 или вектор
или вектор 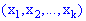 , т.е. на множестве
, т.е. на множестве  есть определенная функция
есть определенная функция 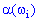 , которая для каждого элементарного события
, которая для каждого элементарного события 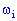 находит элемент одномерного пространства
находит элемент одномерного пространства 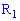 или
или 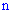 - мерного пространства
- мерного пространства 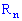 .
.
Эту функцию называют случайной величиной. В случае, когда 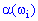 отражает множество
отражает множество  на одномерное пространство
на одномерное пространство 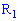 случайную величину называют одномерной. Если отображение осуществляется на
случайную величину называют одномерной. Если отображение осуществляется на 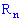 , то случайную величину называют n- мерной (системой n случайных величин или n - мерным случайным вектором).
, то случайную величину называют n- мерной (системой n случайных величин или n - мерным случайным вектором).
Величина называется случайной, если в результате проведения опыта под влиянием случайных факторов она приобретает то или другое возможное числовое значение с определенной вероятностью.
Если множество возможных значений случайной величины является счетно, то ее называют дискретной. В противном случае ее называют непрерывной.
Случайные величины для удобства обозначают прописными буквами латинского алфавита 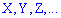 , а их возможные значения - строчными
, а их возможные значения - строчными 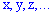 .
.
Для установления случайной величины необходимо знать не только множество возможных ее значений, но и указать, с какими вероятностями она приобретает то или иное возможное значение.
С этой целью вводят понятие закона распределения вероятностей – зависимость, которая устанавливает связь между возможными значениями случайной величины и соответствующими им вероятностями.
Закон распределения дискретной случайной величины  часто задают в табличной форме, функцией, или графически с помощью вероятностного многоугольника.
часто задают в табличной форме, функцией, или графически с помощью вероятностного многоугольника.
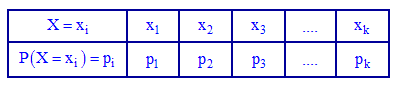
При табличной формы записи закона указывается множество возможных значений случайной величины  находится в порядке их возрастания в первой строке, и соответствующих им вероятностей в следующей:
находится в порядке их возрастания в первой строке, и соответствующих им вероятностей в следующей:
Случайные события должны быть попарно несовместимы и образовывать полную группу, то есть удовлетворять условие:
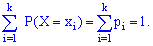
Приведенную зависимость называют условием нормировки для дискретной случайной величины 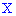 , а таблицу распределения – рядом распределения.
, а таблицу распределения – рядом распределения.
Функция распределения вероятностей и ее свойства
Закон распределения вероятностей можно представить в виде функции распределения вероятностей случайной величины  , которая может использоваться как для дискретных, так и для непрерывных случайных величин.
, которая может использоваться как для дискретных, так и для непрерывных случайных величин.
Функцию аргумента 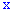 , устанавливающую вероятность случайного события
, устанавливающую вероятность случайного события 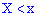 называют функцией распределения вероятностей:
называют функцией распределения вероятностей:
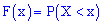
Ее следует понимать как функцию, которая устанавливает вероятность случайной величины, которая может принимать значения, меньше 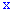 .
.
Функция распределения обладает следующими свойствами:
1. Она всегда положительная со значениями в пределах от нуля до единицы 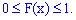
2. Функция является монотонно возрастающей, а именно 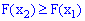 , если
, если 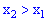 .
.
С этого свойства получают приведенные выводы:
a) Вероятность вступления случайной величиной  возможных значений из промежутка
возможных значений из промежутка  равна прироста ее интегральной функции
равна прироста ее интегральной функции  на этом промежутке:
на этом промежутке:
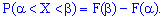
б) Вероятность, что непрерывная случайная величина  примет конкретное возможное значение, всегда равна нулю
примет конкретное возможное значение, всегда равна нулю
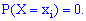
Для непрерывной случайной величины  выполняются такие равенства:
выполняются такие равенства:
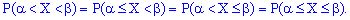
3. На крайних точках непрерывная случайная величина принимает значение 0 и 1.
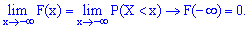
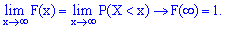
Из этих границ следует, что для дискретной случайной величины  с возможными значениями из ограниченного промежутка
с возможными значениями из ограниченного промежутка  имеем
имеем
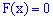 для
для 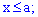
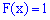 для
для 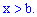
----------------------------
Приведем решения задач на отыскание функции распределения.
Пример 1. Закон распределения дискретной случайной величины  задан таблицей:
задан таблицей:
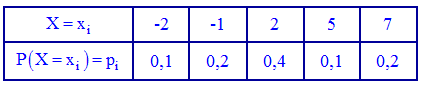
Построить функцию распределения  и ее график.
и ее график.
Решение. Согласно свойствами функции  получим приведенные дальше значение.
получим приведенные дальше значение.
1) 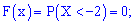
2) 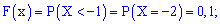
3) 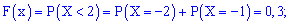
4) 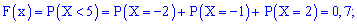
5) 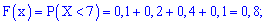
6) 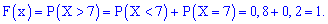
Компактно функция распределения  иметь запись
иметь запись
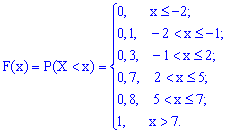
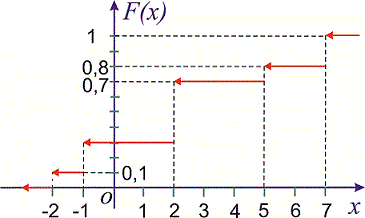
График функции распределения  изображен на рисунке ниже
изображен на рисунке ниже
----------------------------
Пример 2. Есть три коробки с шарами. В первой содержится 6 желтых и 4 синие шарики, во втором - 7 желтых и 3 синие, а в третьем - 2 желтых и 8 синих. Из каждой коробки наугад берут по одному шарику. Построить закон распределения вероятностей дискретной случайной величины  – появления числа синих шариков среди трех наугад взятых, определить закон распределения
– появления числа синих шариков среди трех наугад взятых, определить закон распределения  и построить график этой функции.
и построить график этой функции.
Решение. Среди трех наугад взятых шариков число синих может быть 0, 1, 2, 3.
В табличной форме закон распределения дискретной случайной величины имеет вид:

Вычислим вероятности 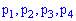 . С этой целью обозначим
. С этой целью обозначим 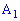 - случайное событие, заключающееся соответственно в появлении желтого шарики и
- случайное событие, заключающееся соответственно в появлении желтого шарики и  – появление синего с первой коробки. Подобным образом для остальных коробок
– появление синего с первой коробки. Подобным образом для остальных коробок 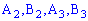 . Вероятности этих событий такие:
. Вероятности этих событий такие:
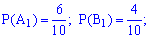
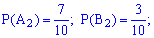
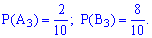
Поскольку случайные события 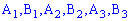 независимы, то вероятности находим по формулам:
независимы, то вероятности находим по формулам:
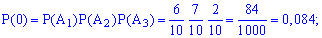
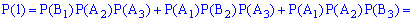
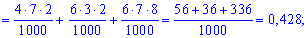
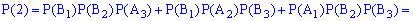
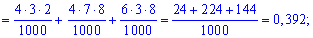
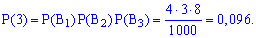
Вычисление достаточно просты и сделаны обозначения полностью все объясняют. Проверим выполнение условия нормировки
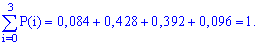
Всегда выполняйте проверку данного условия: это достаточно просто сделать и позволяет быстро проверить правильность вычислений вероятности. В случаях, когда условие нормировки не выполняется нужно отыскать ошибку и исправить ее.
У нас же все вычисления правильны, потому записываем закон распределения вероятностей в табличной форме:

Вычисляем значение интегральной функции
1) 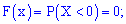
2) 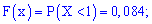
3) 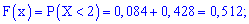
4) 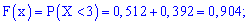
5) 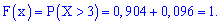
В случае ошибок при нахождении вероятностей последнее соотношение дает отличный от единицы результат, поэтому можете проверять и по этому значению. Упрощенно функция распределения будет иметь вид
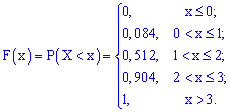
а ее график следующий
----------------------------
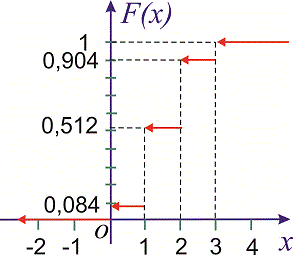
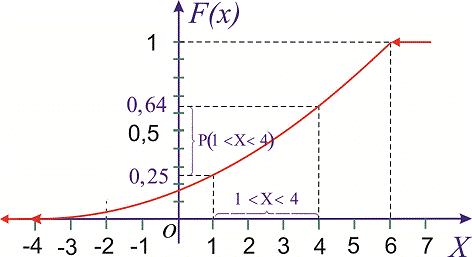
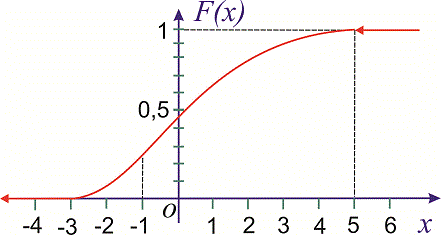
Пример 3. Закон распределения случайной величины 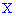 задан функцией распределения вероятностей
задан функцией распределения вероятностей
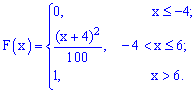
Построить график функции распределения  и вычислить вероятность, что случайная величина принадлежит промежутку
и вычислить вероятность, что случайная величина принадлежит промежутку 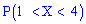 .
.
Решение. Функция распределения будет иметь вид.
Используя определение, вычислим
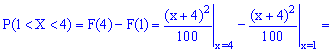
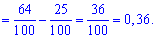
Таким образом вероятность, что случайная величина принадлежит промежутку [1,4] равна 0,36.
----------------------------
Внимательно разберитесь с приведенными примерами нахождения функции распределения, это Вам пригодится на практических занятиях. Старайтесь проверять условие нормирования, чтобы избежать дальнейших ошибок и правильно определяйте вероятности.
----------------------------------------------
]]>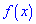 .
.
Плотностью вероятностей случайной величины 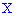 называют первую производную от интегральной функции распределения вероятностей
называют первую производную от интегральной функции распределения вероятностей 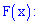
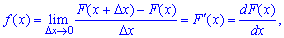
откуда дифференциал 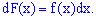
Поскольку прирост определяют зависимости
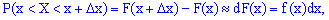
куплена плотности вероятностей на прирост случайной величины 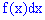 соответствует вероятность того, что случайная величина
соответствует вероятность того, что случайная величина 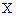 содержаться в промежутке
содержаться в промежутке 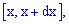 где
где 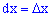 .
.
Геометрически на графике плотности вероятностей 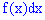 соответствует площадь прямоугольника с основанием
соответствует площадь прямоугольника с основанием 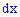 и высотой
и высотой 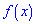
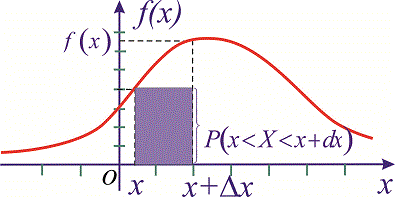
Свойства плотности вероятностей
1. Плотность вероятностей принимает положительные значения 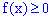 . Это свойство следует из определения первой производной от функции распределения
. Это свойство следует из определения первой производной от функции распределения 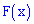 , которая в свою очередь является неубывающей функцией.
, которая в свою очередь является неубывающей функцией.
2. Условие нормирования случайной величины 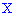
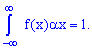
3.Вероятность попадания случайной величины в промежуток 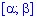 определяется зависимостью
определяется зависимостью
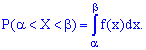
4. Функция распределения вероятностей непрерывной случайной величины определяется через плотность распределения вероятностей интегрированием
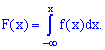
---------------------------------------
Рассмотрим задачи для закрепления материала на практике.
Пример 1. Закон распределения случайной величины 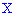 заданы функцией
заданы функцией
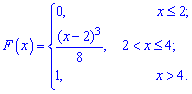
Найти плотность распределения вероятностей 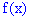 и построить графики обеих функций
и построить графики обеих функций 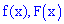 . Вычислить вероятность того, что случайная величина принадлежит промежутку
. Вычислить вероятность того, что случайная величина принадлежит промежутку 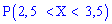
Решение. Вычисляем функцию плотности вероятностей
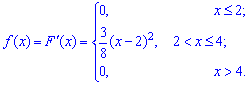
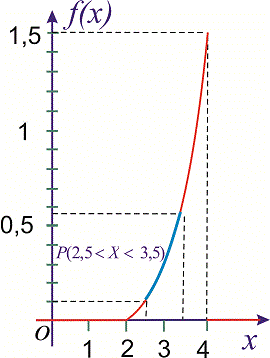
Графики функций  изображены на рисунках
изображены на рисунках
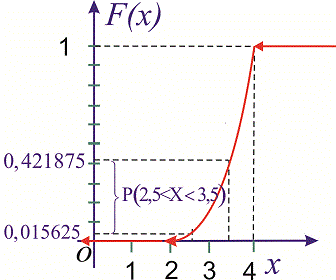
Вероятность события 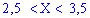 вычислим по формуле
вычислим по формуле
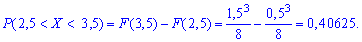
Согласно приведенной выше формулы получим
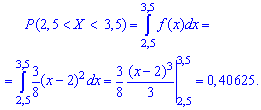
На этом задача решена.
--------------------------------------------
Пример 2. По заданной функцией плотности распределения вероятностей
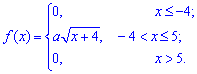
установить параметры  и функцию распределения вероятностей
и функцию распределения вероятностей 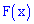 . Построить графики функций
. Построить графики функций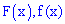 .
.
Решение. Значение постоянной  определяем из условия нормировки
определяем из условия нормировки
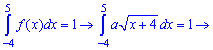
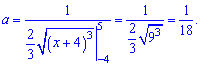
При найденном значении  плотность вероятностей будет иметь вид
плотность вероятностей будет иметь вид
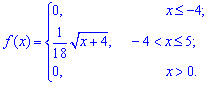
Функция распределения вероятностей определяется интегрированием:

Записываем общий вид функции 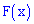 ,
,
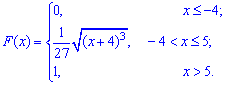
Графики функций распределения вероятностей и ее плотности показаны на рисунках ниже
---------------------------------------
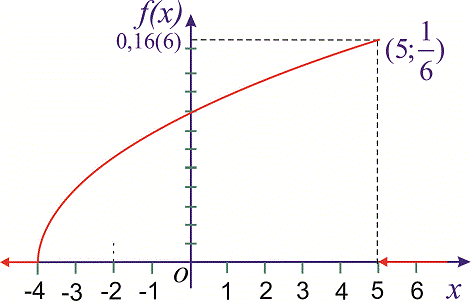
Пример 3. Случайная величина  имеет закон распределения вероятностей в виде треугольника
имеет закон распределения вероятностей в виде треугольника
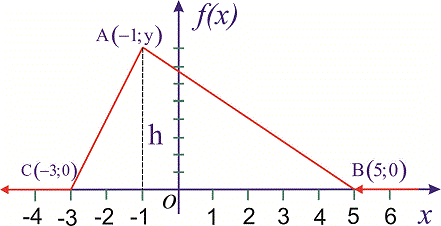
Записать выражения для плотности вероятностей и функции распределения вероятностей, построить график 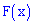 и вычислить
и вычислить 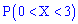 .
.
Решение. На промежутках 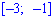 и
и 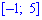 плотность вероятностей меняется по линейному закону вида
плотность вероятностей меняется по линейному закону вида
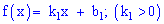
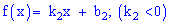
для первого и второго участки соответственно. Для нахождения неизвестных констант 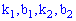 установим ординаты вершины треугольника
установим ординаты вершины треугольника 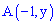 . Используем условие нормирования, согласно которому площадь треугольника
. Используем условие нормирования, согласно которому площадь треугольника 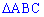 равна единице:
равна единице:
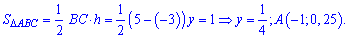
При известных координатах всех вершин находим уравнение прямых
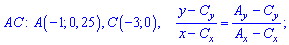
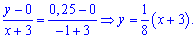
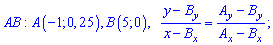
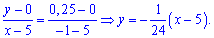
Есть другой способ нахождения уравнения прямых, предусматривающий отыскания по одной константе на уравнение. Если известна точка пересечения прямой с осью ординат 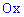 , то уравнение прямой которая через эту точку проходит следующее
, то уравнение прямой которая через эту точку проходит следующее
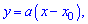
где 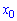 – ордината пересечения с осью
– ордината пересечения с осью 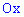 . Подстановкой второй точки прямой находят неизвестную константу
. Подстановкой второй точки прямой находят неизвестную константу  . Для заданных точек получим
. Для заданных точек получим
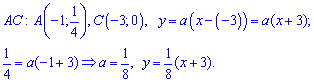
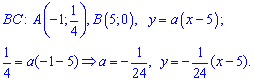
Со временем второй метод для Вас станет проще и практичнее в использовании. Плотность вероятностей примет значение
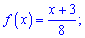
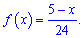
а ее функция примет вид
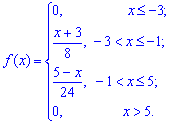
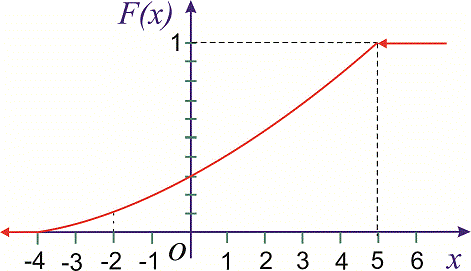
Функцию распределения вероятностей 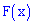 находим интегрированием:
находим интегрированием:
а) на промежутке 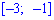 :
:
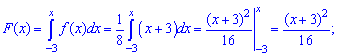
2) на промежутке 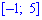
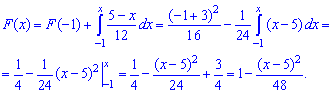
Следовательно, функция распределения вероятностей такая
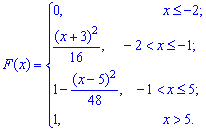
Ее график приведен ниже
Вычисляем вероятность события 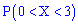 согласно формуле
согласно формуле
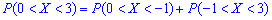
или
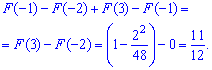
Следовательно, вероятность равна
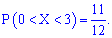
-------------------------
Хорошо проанализируйте приведенные примеры - это поможет научиться быстро находить плотность распределения вероятностей и выполнять построение графика. Будьте внимательны при интегрировании и выбирайте удобную для вычислений методику.
]]>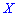 . Рассчитывать его не так трудно, особенно если имеем дискретную величину с небольшим количеством точек.
. Рассчитывать его не так трудно, особенно если имеем дискретную величину с небольшим количеством точек.
Математическим ожиданием случайной величины 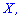 определенной на дискретном множестве значений называется величина, равная сумме попарных произведений величин
определенной на дискретном множестве значений называется величина, равная сумме попарных произведений величин 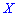 на их вероятности появления
на их вероятности появления
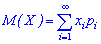
Если множество ограничено, то нужно искать сумму числа слагаемых
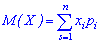
Если множество 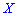 является непрерывным, то математическое ожидание случайной величины
является непрерывным, то математическое ожидание случайной величины 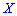 определяется интегрированием по формуле
определяется интегрированием по формуле
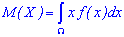
Если 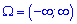 , то
, то
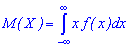
Если 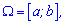 то
то
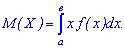
Свойства математического ожидания
1. Математическое ожидание от постоянной величины 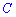 равно постоянной
равно постоянной
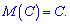
2. Постоянный множитель при случайной величине можно выносить за скобки
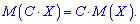
Для дискретной случайной величины справедлива зависимость
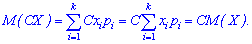
Для непрерывной следующая:
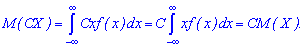
3. Если 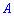 и
и  являются постоянными величинами, то справедливая зависимость
являются постоянными величинами, то справедливая зависимость
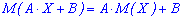
Для дискретной случайной величины:
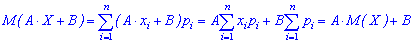
Для непрерывной случайной величины:
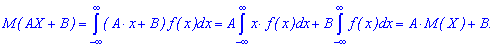
-------------------------
Приведем решения распространенных на практике задач.
Пример 1. Закон распределения дискретной случайной величины задан таблично:
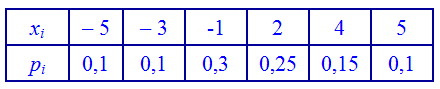
Вычислить математическое ожидание.
Решение. Согласно приведенной выше формулы, вычисляем
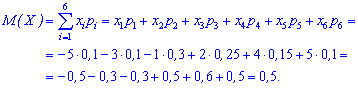
Таким образом, найдено математическое ожидание равное 0,5.
-------------------------
Пример 2. По заданной функцией плотности вероятностей
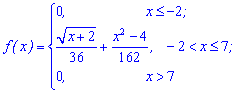
вычислить математическое ожидание.
Решение. Согласно формулы для непрерывной случайной величины проводим интегрирование
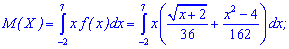
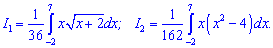
Найдем интегралы по очереди, для первого выполним замену переменных
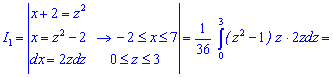
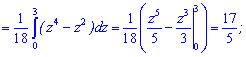
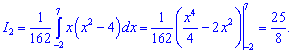
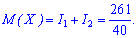
-------------------------
Пример 3. Плотность вероятностей задано тригонометрической формулой
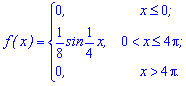
Найти математическое ожидание.
Решение. Проводим интегрирования по частям
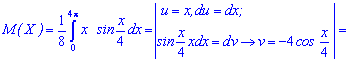
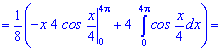
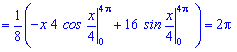
Найдено математическое ожидание равно 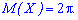
-------------------------
Пример 4. По заданной функцией распределения вероятностей
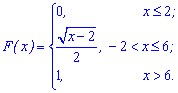
вычислить математическое ожидание.
Решение. Для вычисления 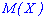 необходимо сначала найти плотность вероятностей. Для этого осуществляем дифференцирования функции распределения
необходимо сначала найти плотность вероятностей. Для этого осуществляем дифференцирования функции распределения
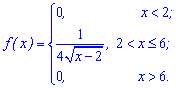
После этого проводим интегрирование по уже формуле:
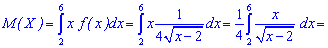
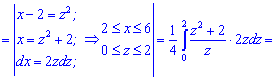
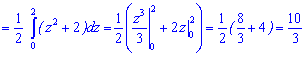
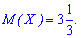
--------------------------
Для проверки правильности вычислений запомните, что если случайная величина принадлежит промежутку 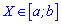 , то математическое ожидание
, то математическое ожидание 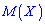 также должно находиться внутри
также должно находиться внутри 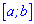 , выполняя роль центра распределения этой величины. В случаях когда найдено математическое ожидание выходит за пределы промежутка нужно проанализировать предварительные вычисления и исправить ошибки. Будьте внимательны при интегрировании функций и замене переменных, именно в этом скрыта львиная доля Ваших ошибок.
, выполняя роль центра распределения этой величины. В случаях когда найдено математическое ожидание выходит за пределы промежутка нужно проанализировать предварительные вычисления и исправить ошибки. Будьте внимательны при интегрировании функций и замене переменных, именно в этом скрыта львиная доля Ваших ошибок.
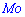 дискретной случайной величины
дискретной случайной величины 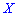 называют те ее возможное значение, которые соответствует наибольшей вероятности появления (т.е. такое значение величины
называют те ее возможное значение, которые соответствует наибольшей вероятности появления (т.е. такое значение величины 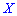 , которое случается чаще всего при проведении экспериментов, опытов, наблюдений). В случае случайной величины модой называют то ее возможное значение, которому соответствует максимальное значение плотности вероятностей
, которое случается чаще всего при проведении экспериментов, опытов, наблюдений). В случае случайной величины модой называют то ее возможное значение, которому соответствует максимальное значение плотности вероятностей
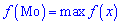
В зависимости от вида функции 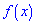 случайная величина
случайная величина 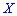 может иметь разное количество мод. Если случайная величина имеет одну моду, то такое распределение вероятностей называют одномодальным; если распределение имеет две моды — двухмодальным и более – мультимодальным.
может иметь разное количество мод. Если случайная величина имеет одну моду, то такое распределение вероятностей называют одномодальным; если распределение имеет две моды — двухмодальным и более – мультимодальным.
Существуют и такие распределения, которые не имеют моды, их называют антимодальными. Медианой  случайной величины
случайной величины 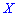 называют то ее значения, для которого выполняются равенство вероятностей событий, то есть, плотность вероятностей справа и слева одинаковы и равны половине (0,5)
называют то ее значения, для которого выполняются равенство вероятностей событий, то есть, плотность вероятностей справа и слева одинаковы и равны половине (0,5)
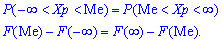
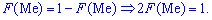
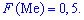
Графически мода и медиана изображенные на рисунке
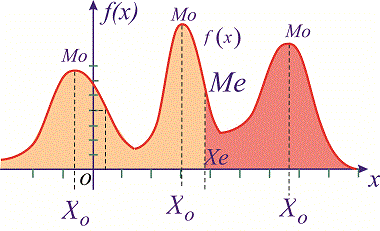
При таком значению случайной величины график функции распределения делится на части с одинаковой площадью. Непрерывная случайная величина имеет только одно значение медианы. Для дискретной случайной величины медиану обычно не определяют, однако в некоторой литературе приводятся правила, согласно которым, для ряда случайных величин размещенных в порядке возрастания (вариационного ряда) моду определяют распределения: если есть нечетное количество случайных величин 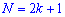 то медиана равна средней величине
то медиана равна средней величине
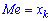
в случае четного количества 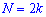 полусумме средних величин
полусумме средних величин
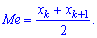
Рассмотрим примеры определения моды и медианы.
Пример 1. В развлекательном центре работник обслуживает четыре дорожки для боулинга. Вероятность того, что какая-то дорожка нуждается в уборке в течение смены является постоянной величиной с вероятностью 85%.
Построить закон распределения вероятностей дискретной случайной величины 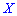 — количество дорожек, которые требуют уборки. Найти моду
— количество дорожек, которые требуют уборки. Найти моду 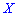 .
.
Решение. Случайной величина может принимать значения
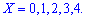
Вероятности появления значений определяем по образующей функцией
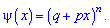
Для заданной задачи входные величины принимают значения
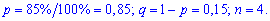
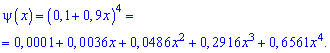
Искомые вероятности входят множителями при степенях аргумента
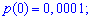
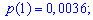
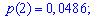
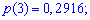
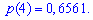
Закон распределения вероятностей запишем в виде таблицы
С таблице определяем моду 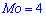 , как значение при максимальной вероятности. Получили одномодальное распределение
, как значение при максимальной вероятности. Получили одномодальное распределение
Пример 2. По заданной плотностью вероятностей
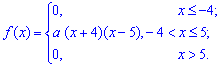
найти параметр  , плотность вероятностей
, плотность вероятностей 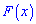 , моду
, моду 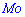 .
.
Решение. Применяя условие нормирования выполняем интегрирование
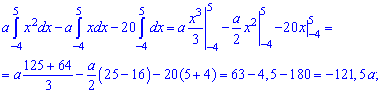
после того определяем параметр
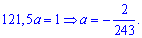
Плотность вероятностей, учитывая найденное значение будет иметь вид
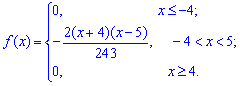
а ее график изображен на рисунке ниже
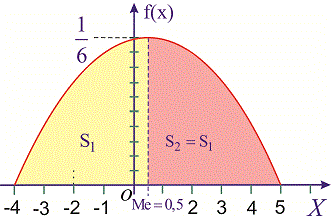
Из графика плотности вероятностей видим, что мода принимает значение 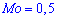 . Определим медиану
. Определим медиану  с помощью функции распределения вероятностей. Ее значение на промежутке
с помощью функции распределения вероятностей. Ее значение на промежутке  находим интегрированием
находим интегрированием
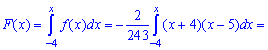
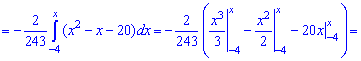
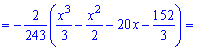
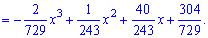
Функция распределения иметь следующий вид
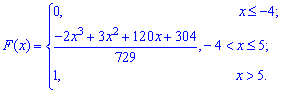
а ее график будет иметь вид
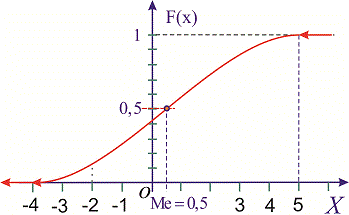
Для определения медианы случайной величины  применяем формулу
применяем формулу
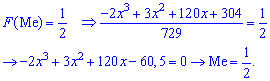
Медиану  можно найти с помощью плотности вероятностей
можно найти с помощью плотности вероятностей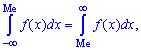
для дискретной случайной величины из промежутка 
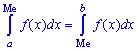
Таким образом медиану  — возможное значение случайной величины
— возможное значение случайной величины 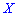 , при котором прямая, проведенная перпендикулярно соответствующей точки на плоскости
, при котором прямая, проведенная перпендикулярно соответствующей точки на плоскости 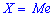 , делит площадь фигуры, ограниченной функцией плотности вероятностей
, делит площадь фигуры, ограниченной функцией плотности вероятностей 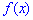 на две равные части.
на две равные части.
-------------------------------
Задача на определение моды и медианы случайной величины встречаются на практике не так часто, как плотности распределения вероятностей, однако вышеприведенный теоретический материал и решения распространенных примеров помогут Вам находить эти величины без больших затрат времени. При необходимости Вы всегда можете заказать решение задач по теории вероятностей в нас.
]]>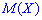 может соответствовать множество случайных величин, будут различаться не только возможными значениями, но и характером распределения и самой природой возможных значений.
может соответствовать множество случайных величин, будут различаться не только возможными значениями, но и характером распределения и самой природой возможных значений.
Например. Законы распределения двух случайных величин 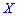 и
и 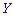 заданные таблицами:
заданные таблицами:

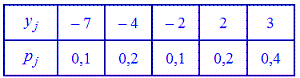
Вычислить математическое ожидание 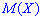 и
и 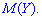
Решение. Находим математическое ожидание по класической формуле
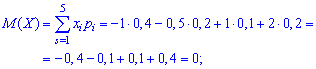
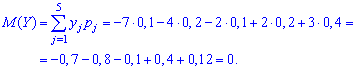
Получили, что для двух различных законов распределения математическое ожидание принимает одинаковое значения (0), при этом возможные значения случайных величин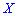 и
и 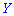 различаются. Из приведенного примера видно, что в случае равенства математических ожиданий
различаются. Из приведенного примера видно, что в случае равенства математических ожиданий 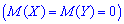 случайные величин
случайные величин 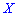 и
и 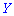 имеют тенденцию к колебаниям относительно
имеют тенденцию к колебаниям относительно 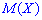 и
и 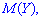 причем
причем 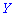 имеет больший размах рассеяния относительно
имеет больший размах рассеяния относительно 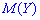 сравнительно случайной величине
сравнительно случайной величине 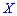 относительно
относительно 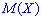 . Поэтому математическое ожидание еще называют центром рассеяния. Для определения рассеяния вводится числовая характеристика, называемая дисперсией.
. Поэтому математическое ожидание еще называют центром рассеяния. Для определения рассеяния вводится числовая характеристика, называемая дисперсией.
Для определения дисперсии рассматривается отклонение случайной величины 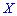 от своего математического ожидания
от своего математического ожидания 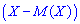
Математическое ожидание такого отклонения случайной величины 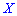 всегда равна нулю. В этом легко убедиться из следующего соотношения
всегда равна нулю. В этом легко убедиться из следующего соотношения
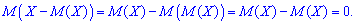
Таки образом, отклонение не может быть мерой рассеивания случайной величины.
Дисперсией случайной величины 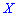 называют математическое ожидание квадрата отклонения случайной величины
называют математическое ожидание квадрата отклонения случайной величины 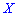 от своего математического ожидания
от своего математического ожидания 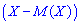
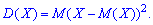
Для дискретной случайной величины 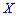 дисперсия вычисляется по формуле
дисперсия вычисляется по формуле
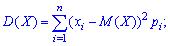
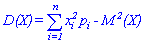
для непрерывной находят интегрированием
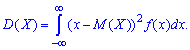
Если непрерывная величина заданная на интервале 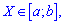 то дисперсия равна интегралу с постоянными пределами интегрирования
то дисперсия равна интегралу с постоянными пределами интегрирования
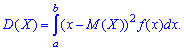
Дисперсия обладает следующими свойствами
1. Если случайная величина состоит из одной тотчки 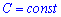 — постоянная величина, то дисперсия равна нулю
— постоянная величина, то дисперсия равна нулю
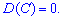
2. Дисперсия от произведения постоянной на случайную величину равна квадрату постоянной умноженной на дисперсию случайной величины
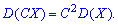
3. Если 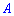 и
и  — постоянные величины, то для дисперсии
— постоянные величины, то для дисперсии 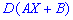 справедлива зависимость
справедлива зависимость
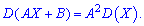
Это следует из двух предыдущих свойств.
Дисперсию можно вычислить по упрощенной формуле:
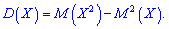
которая в случае дискретной случайной величины 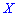 имеет вид
имеет вид
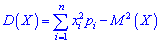
для непрерывной определяется зависимостью
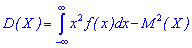
и для непрерывной на промежутке 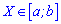 соотношением
соотношением
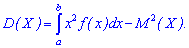
Приведенные формулы очень удобны в вычислениях, и их, в отличие от предыдущих, используют в обучении
Также следует помнить, что дисперсия всегда принимает неотрицательные значения 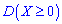 . Она характеризует рассеяние случайной величины относительно своего математического ожидания. Если случайная величина измерена в некоторых единицах, то дисперсия будет измеряться в этих же единицах, но в квадрате.
. Она характеризует рассеяние случайной величины относительно своего математического ожидания. Если случайная величина измерена в некоторых единицах, то дисперсия будет измеряться в этих же единицах, но в квадрате.
Для сравнения удобно пользоваться числовыми характеристиками одинаковой размерности случайной величиной. Для этого вводят в рассмотрение среднее квадратичное отклонение – корень квадратный из дисперсии. Ее обозначают греческой буквой «сигма»
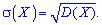
----------------------------------------
Рассмотрим примеры для ознакомления с практической стороной определения этих величин.
Пример 1. Закон распределения дискретной случайной величины 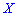 заданы таблицей:
заданы таблицей:

Вычислить дисперсию 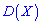 и среднее квадратическое отклонение
и среднее квадратическое отклонение 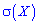 .
.
Решение. Согласно свойствами дисперсии получим:
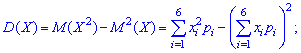
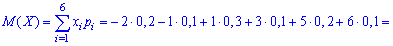
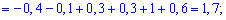
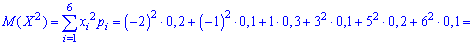
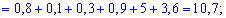
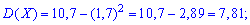
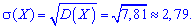
----------------------------------------
Пример2. Есть четыре электрические лампочки, каждая из которых имеет дефект с вероятностью 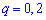 (
(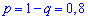 — вероятность того, что лампочка без дефекта). Последовательно берут по одной лампочке, вкручивают в патрон и включают электрический ток. При включении тока лампочка может перегореть, и ее заменяют на другую. Построить закон распределения дискретной случайной величины
— вероятность того, что лампочка без дефекта). Последовательно берут по одной лампочке, вкручивают в патрон и включают электрический ток. При включении тока лампочка может перегореть, и ее заменяют на другую. Построить закон распределения дискретной случайной величины 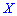 — число лампочек, которые будут опробованы. Вычислить среднее квадратическое отклонение
— число лампочек, которые будут опробованы. Вычислить среднее квадратическое отклонение 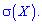
Решение. Дискретная случайная величина 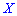 — число лампочек, которые будут опробованы - приобретает такие возможных значений:
— число лампочек, которые будут опробованы - приобретает такие возможных значений:
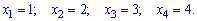
Вычислим соответствующие вероятности:
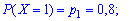
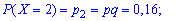
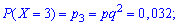
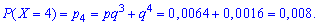
Последнюю вероятность можно трактовать следующим образом: четвертая лампочка будет испытана, когда третья перегорит, а четвертая - нет, или если и четвертая перегорит.
В табличной форме закон распределения 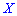 иметь следующий вид:
иметь следующий вид:
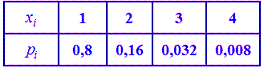
Для нахождения среднего квадратического отклонения найдем сначала значение дисперсии. Для дискретной случайной величины она примет значение:
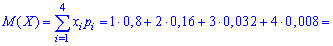
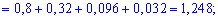
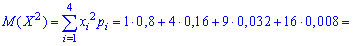
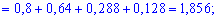
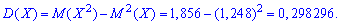
Среднее квадратичное отклонение находим добычей корня квадратного из дисперсии.
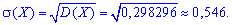
----------------------------------------
Пример 3. Закон распределения вероятностей дискретной случайной величины  заданы в виде функции
заданы в виде функции
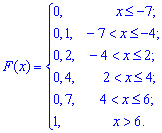
Вычислить среднее квадратическое отклонение и дисперсию 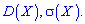
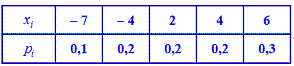
Решение. С помощью функции распределения вероятностей формируем закон распределения в виде таблицы
На основе таблицы распределения вычисляем дисперсию
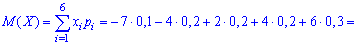
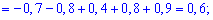
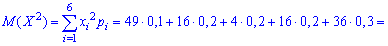
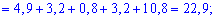
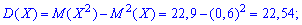
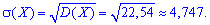
-----------------------
Подобных примеров можно привести множество, основная их суть в правильном применении приведенных в начале статьи формул для вычисления дисперсии и математического ожидания. Применяйте их там где это необходимо и не допускайте ошибок при определении дисперсии.
]]>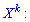
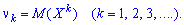
Когда 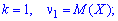
Когда 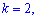
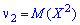 и т. д.
и т. д.
Для дискретной случайной величины 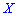 начальные моменты определяют зависимостью
начальные моменты определяют зависимостью
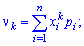
для непрерывной интегрированием
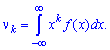
Если непрерывная величина задана интервалом 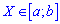 , то моменты вычисляют по формуле
, то моменты вычисляют по формуле
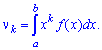
Центральным моментом k-го порядка называют математическое ожидание от величины 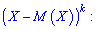
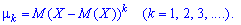
Когда 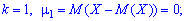
для 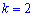 имеем
имеем 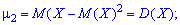
при 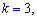
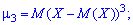
при 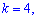
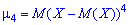
и так далее.
Для дискретной случайной величины центральные моменты вычисляют по формуле
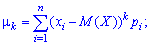
для непрерывной по следующей
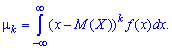
Если случайная величина определена интервалом 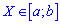 , то центральные моменты определяют интегрированием
, то центральные моменты определяют интегрированием
Рассмотрим пример отыскания приведенных величин.
-----------------------------------
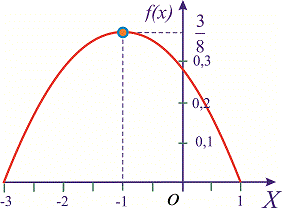
Пример 1. Задана функция плотности вероятностей
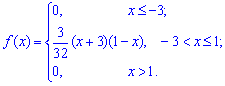
Вычислить начальные и центральные моменты второго и третьего порядка 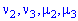 .
.
Решение. Для вычисления начальных моментов выполним интегрирование по вышеприведенным формулам
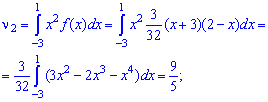
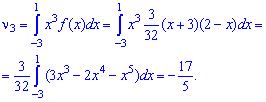
Промежуточные операции при интегрировании пропущены, они занимают много места, а Вам главное иметь инструкцию для вычислений, так как примеры у Вас будут другие.
Для вычисления центральных моментов инерции необходимо знать математическое ожидание случайной величины, поэтому определяем его первее
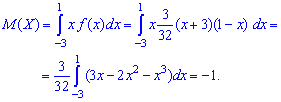
Найдено математическое ожидание подставляем в формулу центральных моментов. В случае 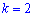 получим
получим
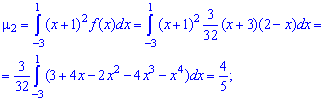
и при 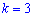 будем иметь
будем иметь
На этом решения примера завершено, функция плотности вероятностей приведена на графике
-----------------------------------
Примеры нахождения начальных и центральных моментов будут рассмотрены в следующей статье. Задачи совсем не сложные, а вычисления величин сводится к возведения в степень, интегрирование, умножение и суммирование.
]]>