С данной статьи начинаем цепочку публикаций, которые научат Вас находить особенности в границах, классифицировать неопределенности и применять правильную методику раскрытия. Дело заключается в том, что разработано много правил и приемов, которые позволяют по виду заданной функции или последовательности быстро сориентироваться как находить предел. Однако при изучении теоретического материала или на практических занятиях Вам или на этом не отмечают, или Ваши мысли гуляют за пределами аудитории.
Для охвата всего материала мы собрали много примеров из студенческой практики, модулей, контрольных, заказов и попытаемся здесь разъяснить, как и в каких случаях применять приведенные алгоритмы.
Пример 1. Вычислить предел последовательности:
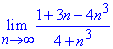
Решение: При подстановке бесконечности получим неопределенность вида бесконечность разделить на бесконечность (∞/∞). Разделим числитель и знаменатель на переменную в наибольшей степени и сократим на нее. В результате избавимся от неопределенности, а слагаемые что останутся, будут стремиться к нулю при больших номерах последовательности
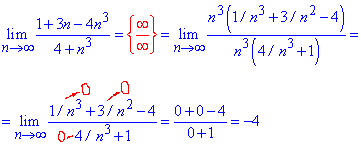
Все числа, что останутся и укажут куда стремится предел.
Пример 2. Вычислить предел последовательности:
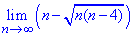
Решение: При прямой подстановке бесконечно большого номера получим неопределенность бесконечность минус бесконечность (∞-∞).
Правило раскрытия такого типа неопределенности хорошо расписано в литературе и заключается в умножении и разделении неопределенности на множитель, сопряженный к ней.
Как правило, такие примеры содержат корни и чтобы их лишиться используем умножение на сопряженный множитель, что приводит к разности квадратов или кубов, в то время в знаменателе (или числителе) получим выражение с корнем, которое не содержит неопределенности.
Далее из числителя и знаменателя выделяем доминирующий множитель и упрощаем на него.
Все числа, что останутся и составят предел последовательности.
На языке формул этому отвечает запись
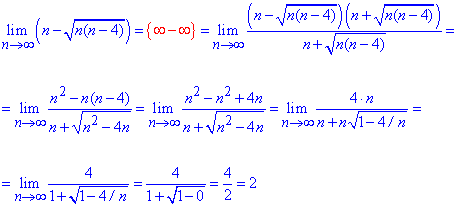
Пример 3. Найти предел функции:
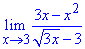
Решение: При подстановке x=3 получим неопределенность 0/0.
Это означает, что и числитель и знаменатель содержат особенность.
Для раскрытия неопределенности выделим в числителе (x-3), а знаменатель умножим и разделим на сопряженное выражение 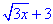 .
.
В результате получим множитель (x-3), на который упрощаем дробь. Далее предел вычисляется методом подстановки переменной
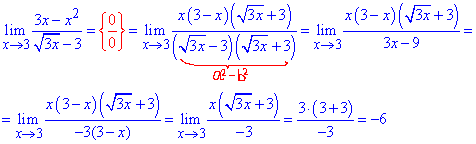
Пример 4. Найти предел функции:
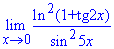
Решение: Задание для большинства студентов чрезвычайно сложное, а все потому что необходимо свести неопределенность типа 0/0 до известных случаев.
В результате преобразования функций получим выражения вида ln(1+x)/x, tan(x)/x, sin(x)/x при переменной стремящейся к нулю.
Далее выделяем первую замечательный предел и ее следствие, затем расписываем через произведение известных пределов.
Все остальное сводится к произведению единиц и отдельного множителя, который и является пределом заданной функции.
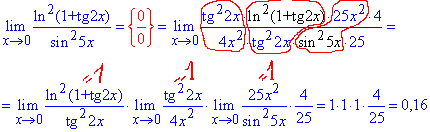
Внимательно разберите приведенный пример, он Вас многому научит.
На практике довольно трудно найти условие, которое бы объединяла несколько формул, поэтому учитесь на сложных примерах.
Тогда точно не будет сложностей в исчислении простых примеров.
Пример 5. Вычислить предел функции:
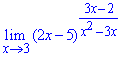
Решение: Подстановка 3 в функцию дает особенность вида единица в степени бесконечность (1^∞). Для ее раскрытия и в функции в скобках, и в дроби, что является показателем выделяем часть, что вносит особенность (х-3).
Далее, для упрощения манипуляций с выражениями делаем замену переменных x-3=t, новая переменная при этом стремится к нулю.
После этого выделяем второй замечательный предел и ищем лимит показателя, что остался.
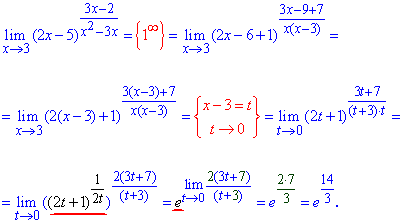
На этом разбор распространенных примеров, которые распространены в учебной практике не завершается.
В соседней публикации будут проанализированы новые алгоритмы вычислений, и примеры пределов функций та последовательностей, которые помогут Вам быстрее освоить теоретический материал и подготовиться к контрольной, модулю, экзамене.


