Проанализируем ответы из курсовых робот, которые будут полезными для Вас в курсе высшей математики. В этот раз разберем 14 новых заданий с особенностями, раскрытие которых возможно при знании методов раскрытия иррацыональностей, сокращения дробей на доминантный множитель, первого и второго замечательных пределов и их следствий, разложения функций в ряд Тейлора и еще несколько приемов. Перечисление в одном предложении большого количества способов избавиться от неопределенности пределов на одних студентов нагоняет страх и панику, однако следующие ответы докажут, что на практике все гораздо проще, если знать ряд правил.
Пример 21 Вычислить предел последовательности:
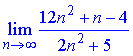
Решение: Для вычисления предела частки полиномов выносим n^2 из числителя и знаменателя дроби и упрощаем на них.
В итоге останутся числа и бесконечно малые величины. Лимит последовательности равный доле постоянных (=6).
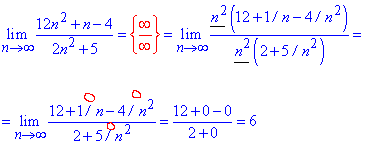
Попробуйте самостоятельно этот же пример вычислить по правилу Лопиталя.
Пример 22 Определить лимит последовательности
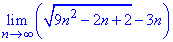
Решение: Предел последовательности вычисляем методом умножения на сопряженное выражение. Таким образом получим разность квадратов и избавимся от корней в числителе.
Далее из числителя и знаменателя дроби выносим n и упрощаем на него. После этого оцениваем дробь при предельном переходе.
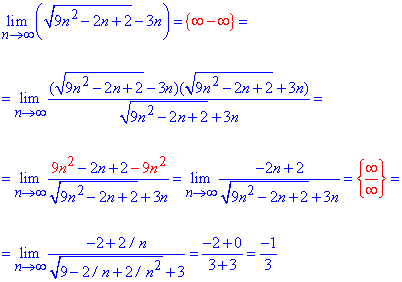
Пример 23 Найти предел функции
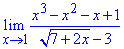
Решение: Лимит функции в точке дает неопределенность вида {0/0}. В числителе полином раскладываем на простые множители, в знаменателе избавляемся от иррациональности умножением на сопряженное выражение. Таким образом избавляемся особенности в знаменателе, однако она остается в числителе. В результате предел функции в точке равен нулю.
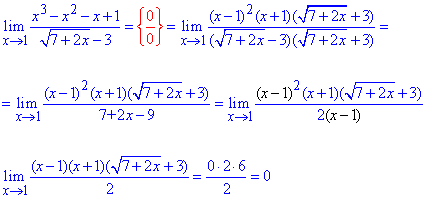
Пример 24 Свести под важные пределы и вычислить
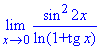
Решение: Предел функции синус логарифма дает особенность {0/0}. Для ее раскрытия следует заданную функцию свести под первый и второй замечательные пределы и их следствия.
Для этого умножуєм и делим на выражения, которых не хватает для применения замечательных пределов. Далее группируем и сводим к произведению пределов, часть из которых равна 1.
Все что останется и составляет предел функции.
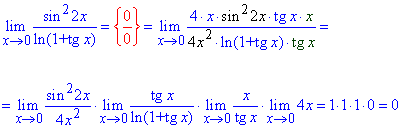
Пример 25 Чему равен лимит функции?
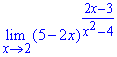
Решение: Функция имеет особенность – единицу в степени бесконечность. Раскрываем ее методом выделения второго замечательного предела, который равен экспоненте.
Для этого выделяем повсюду выражения (x-2), что вносят особенность, а дальше переходим к новой переменной t=x-2.
В показателе выделяем обратный множитель (-1/2t) до слагаемого при единице в скобках (1-2t).
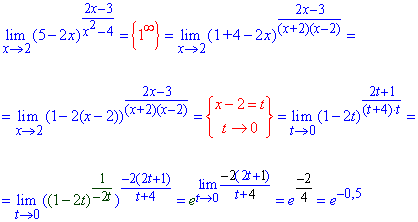
Таким образом, получим экспоненту в степени - лимит функции, что осталась.
Пример 26 Вычислить предел последовательности
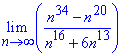
Решение: Если переменная стремится к бесконечности 
, то наибольший вклад вносит переменная в старшем степени. Выделим их в числителе и знаменателе
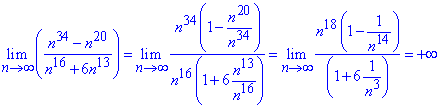
Далее, если в числителе старший степень, то предел стремится к бесконечности.
Пример 27 Найти границу
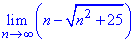
Решение: Если подставить бесконечность в последовательность получим неопределенность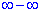 
. Чтобы ее раскрыть, разделим и умножим на выражение, чтобы в числителе получить разность квадратов
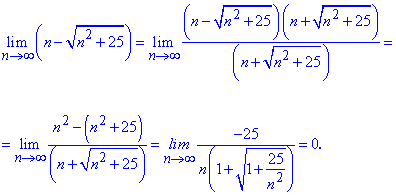
Граница равна нулю, так как степень знаменателя выше степени числителя (1>0).
Пример 28 Вычислить предел последовательности
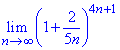
Решение: Задание следует свести под правило второго замечательного предела. Для этого в показателе создаем число, которое является обратно пропорциональным слагаемому возле единички в скобках.
Постоянный множитель при этом и будет показателем экспоненты в пределе
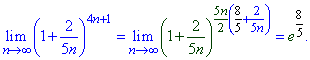
Пример 29 Найти лимит последовательности
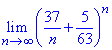
Решение: Поскольку оба значения в скобках меньше единицы (особенно важно 5/63<1), а одно из них, что зависит от номера, стремится к нулю, то их сумма в степени (n) также стремится к нулю
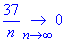
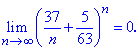
Пример 30. Известно, что лимит последовательности равен 13
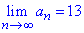
Найти следующий предел
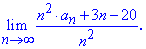
Решение: Выделим в числителе и знаменателе слагаемое, которое вносит наибольший вклад в предел и разделим на него
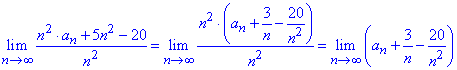
Слагаемые 3/n, -20/n^2 стремятся к нулю при номере стремящемся к бесконечности, поэтому предел равен
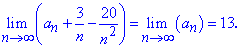
Пример 31 Вычислить предел функции
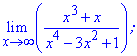
Решение Выделим слагаемое с самым большим показателем и разделим на него
Лимит равен нулю, поскольку степень переменной в знаменателе больше, чем в числителе.
Пример 32 Найти лимит функции
Решение При подстановке единицы в дробь получим неопределенность вида {0/0} .
Чтобы раскрыть неопределенность, выделим в числителе и знаменателе множитель, который пропорционален (x-1) .
Для этого разделим полиномы на указанный множитель.
В результате получим
Далее вносим разложение полиномов в предел и упрощаем
Пример 33 Найти предел функций
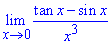
Решение Для раскрытия неопределенности {0/0} воспользуемся эквивалентными бесконечно малыми функциями.
Для этого запишем по два члена разложения tan(x), sin(x) в ряд Тейлора (одного недостаточно, в числителе получим 0)
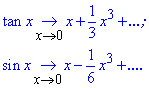
Далее подставим разложения в предел
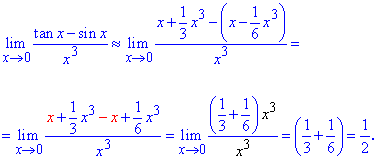
Переменная в кубе упростится и останутся числа, сумма которых и является искомым пределом.
Пример 34 Вычислить предел функции
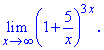
Решение Сведем под правило второго замечательного предела
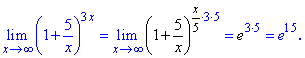
Задача простая, поэтому здесь не на чем останавливаться.
Больше ответов на пределы ищите на страницах сайта.
