Ответы ВНО по математике ищет большое количество участников предстоящего тестирования. Некоторые достаточно сложные, однако идеи для их решения простые и будут Вам полезны. Также можете решать самостоятельно подобные задачи из сборников специально написанных для подготовки к ВНО.
Задача 28. Найдите наименьший положительный период функции
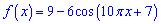
Решение: Период определяется по формуле
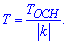
Для синус и косинус функций основной период составляет 2*Пі.
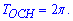
Коэффициент k соответствует множителю при х -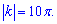 
Вычисляем период
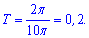
Для наглядности график функции приведен ниже.
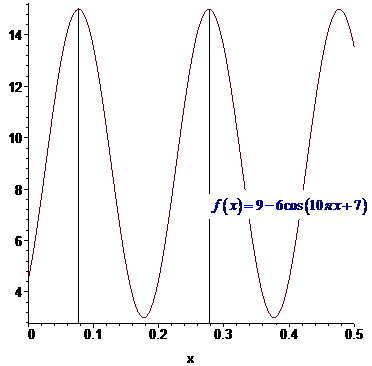
Ответ: 0,2.
------------------------------
Задача 29. В автобусном парке насчитывается n автобусов, шестая часть которых была оборудована информационными табло. Позже информационные табло установило еще на 5 автобусов из имеющихся в парке. После проведенного переоборудования наугад выбирают один из n автобусов парка. Вероятность того ,что это будет автобус с информационным табло составляет 0,25. Определите n . Учтите что каждый автобус оборудуется только одним табло.
Решение: По классическому определению вероятность равна
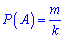
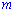– число благоприятных условий,
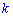– число всех условий события 
.
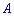Число оборудованных автобусов составляло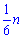 
, а после установки еще пяти стало
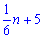
откуда
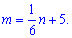
Из условия что вероятность наугад выбрать оборудованный автобус равна 0,25 или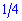 
находим количество автобусов
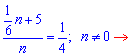
Избавляемся знаменателей
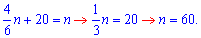
Ответ: 60.
------------------------------
Задача 30. План парковой зоны ограниченной треугольником АВС показано на рисунке. Дуга АВ – велосипедная дорожка. Известно что дуга АВ является четвертой частью окружности радиуса 1,6 км. СА и СВ – касательные к круга (А и В - точки касания). Вычислите площадь изображенной на плане парковой зоны (у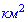 
).
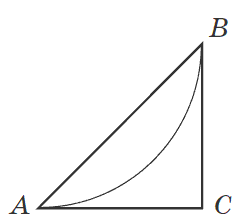
Решение: Площадь треугольника вычисляем по формуле
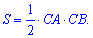
Поскольку CA и CB являются касательными к окружности (по заданию) то они равны радиусу CA=CB=1,6 км. На основе этих даных находим площадь парковой зоны
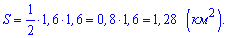
Ответ: 1,28.
------------------------------
Задача 31. На рисунке изображен график функции
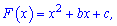
которая является первообразной для функции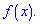 
Определите параметры b и c, найдите функцию 
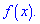В ответе запишите значение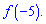 
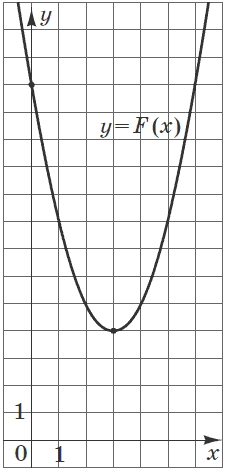
Решение: На рисунке не указана часть графика в которой находится искомая точка, однако видим что это парабола общее уравнение которой имеет вид
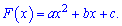
График первообразной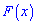 
пересекает ось ординат в точке (0;13), откуда находим F(0)=с=13. Вершина параболы находится в точке с координатами ( 3; 4 ), абсциссу вершины находим по формуле
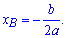
Из графика видно что a=1 – парабола расположена ветками вверх, если вниз то берем a=-1. Абсцисса точки В равна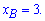
Находим значение параметра
b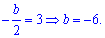 
Уравнение параболы будет иметь вид
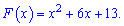
Для отыскания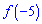 
находим производную от первообразной
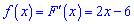
И подставляем искомую точку
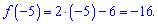
Ответ: - 16.
------------------------------
Задача 32. Основой пирамиды S ABCD является трапеция ABCD 
, длина средней линии которой равна 5 см. Боковое ребро SB перпендикулярно плоскости основания пирамиды и вдвое больше средней линии трапеции ABCD. Найдите расстояние от середины ребра SD до плоскости SBC (в см) , если объем пирамиды равен 
.
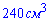Решение: Задача достаточно сложная и мало кто из школьников за нее брался. Приведем графическое построение пирамиды.
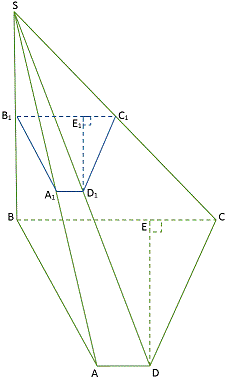
ABCD – по условию трапеция, площадь которой находим по формуле
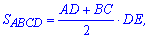
в которой известна
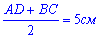
средняя линия, 
– высота трапеции ABCD. Итак площадь основания пирамиды равна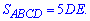 
Объем пирамиды определяется по формуле
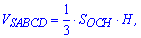
здесь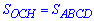 
– площадь основания, 
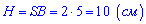– высота пирамиды.
Подставим выражения в формулу объема
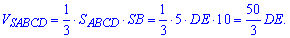
Поскольку объем пирамиды известен и составляет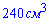 
, то высота 
будет равным
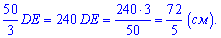
точка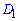 
– середина ребра 
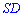. Для вычисления расстояния от точки 
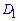до плоскости 
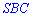, проводим через точку 
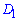сечение пирамиды, которое параллельное ее основанию. Сечением будет подобно основе трапеции 
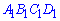. По свойствам пропорций находим
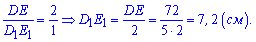
Ответ: 7,2.
------------------------------
Задача 33. Найдите значение параметра а при котором корень уравнения
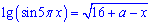
принадлежит промежутку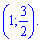 
Решение : Начнем анализ из установки ОДЗ :
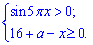
Поскольку корневая функция положительно по определению то левая часть тоже положительная
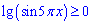
или
Однако синус функция ограниченная
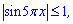
следовательно
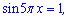
и соответственно левая
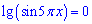
и правая части
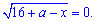
принимают нулевое значение. Решаем первое уравнение
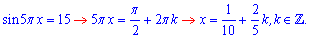
По условию аргумент принадлежит интервалу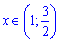 
. Отсюда получим
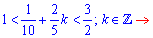
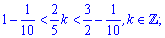
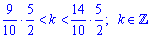
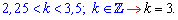
При этом
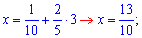
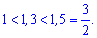
Решаем правую часть
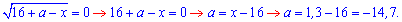
и находим значение параметра.
Ответ: -14,7.
-----------------------------------
Посмотрите решение задач № 22-27 ВНО математика
