Пройти пробный онлайн тест по математике Вы можете на ряде интернет ресурсов, это требует от Вас внимания и времени. Ниже предлагаем ознакомиться с готовыми решениями тестов ВНО по математика за 2013 г. Подобные задачи будут встречаться и при тестированию в 2014 , 2015 и последующих годах.
Задача 16. Упростите выражение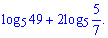 
Варианты ответов :
А) 25;
Б)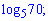 
В)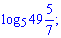 
Г) 
Д) 2.
Решение: Для упрощения выражения применим свойства логарифма. Перепишем первое слагаемое
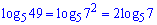
и просуммируем
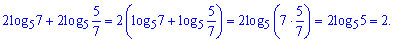
При вычислении подобных выражений нужно хорошо знать свойства логарифмов. Незнание нужного правила может привести к остановке в вычислениях, даже если к результату остается только одно действие. Выпишите все преобразования с логарифмами и старайтесь использовать время от времени на практике.
Ответ: Д).
------------------------------
Задача 17. Меньшая сторона прямоугольника равна 16 м и образует с его диагональю угол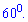 
Середины всех сторон прямоугольника последовательно соединены. Найдите площадь образованного четырехугольника.
Варианты ответов :
А)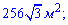 
Б)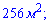 
В)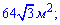 
Г)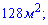 
Д)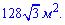 
Решение : Обозначим стороны прямоугольника и известный
угол через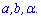 
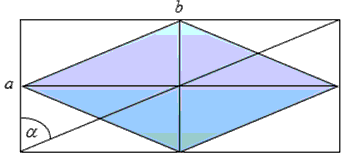
Из прямоугольного треугольника образованного диагональю и сторонами прямоугольника вычислим значение большей стороны по формуле
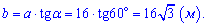
Соединим середины сторон прямоугольника - в результате получим ромб. Кроме этого диагонали ромба по длине равны сторонам прямоугольника и параллельны им. По свойствам ромба его площадь равна
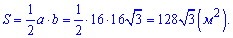
Площадь ромба которая равна половине площади прямоугольника можно без особого труда найти визуально с картинки (если не знаете правила ).
Ответ: Д).
------------------------------
Задача 18. Укажите неравенство которое выполняется для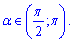 
Варианты ответов :
А)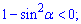 
Б)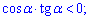 
В)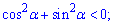 
Г) 
Д)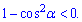 
Решение: Определим значения функций в неравенствах на заданном промежутке. Левая сторона А ) принимает положительное значение
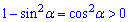
на заданном интервале 
что противоречит заданию. Неравенство Б ) можно упростить и записать в виде
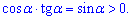
Она также принимает противоположное значение чем указано в задании на интервале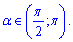 
Неравенство В ) является важной теоремой в тригонометрии и превращается в тождество которое, без сомнения, известно практически всем абитуриентам
Вариант Г ) после упрощения имеет следующий вид
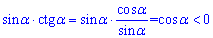
и удовлетворяет условие задачи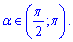 
Последнее неравенство принимает противоположное значение
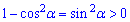
чем указано в вариантах ответов.
Ответ : Г).
------------------------------
Задача 19. В треугольник АВС вписан квадрат KLMN ( см. рисунок ). Высота этого треугольника проведенная к стороне АС равна 6 см. Найдите периметер квадрата если АС =10 см.
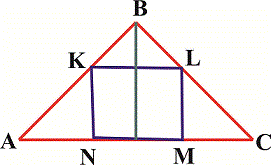
Варианты ответов:
А) 15 см
Б) 7,5 см
В) 12,5 см
Г) 17,5 см
Д) 20 см
Решение: Обозначим через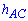 
- высоту треугольника ВСА которою ппроводим к стороне АС, 
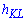– соответственно высота треугольника ВLK к стороне KL. По свойству пропорций имеем
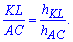
Учитывая что стороны квадрата равны запишем высоту треугольника ВLK в виде
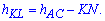
Выполним несложные манипуляции с пропорциями
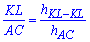
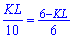
чтобы получить уравнение для определения стороны квадрата
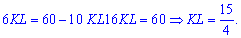
Периметр квадрата находим по известной формуле
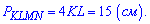
Ответ: А).
------------------------------
Задача 20. Сечение шара плоскостью имеет площадь 81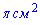
. Найдите расстояние от центра шара до плоскости сечения если радиус шара равен 15 см.
Варианты ответов:
А) 12 см
Б) 8 см
В) 6 см
Г) 9 см
Д) 15 см
Решение: Даную задачу решим на основе следующих соображений. Сечение шара плоскостью всегда дает в сечении круг. Зная формулу площади круга
,
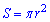с начального условия
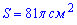
находим его радиус
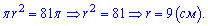
Нарисуем сечение так, чтобы оно сливалось в прямую.
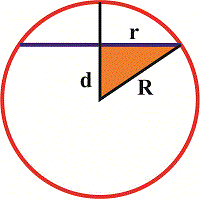
Из прямоугольного треугольника находим нужное расстояние
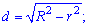
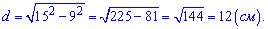
Ответ: А).
------------------------------
Завдання 21. Установите соответствие между фигурой (1-4) и телом вращения (А-Д), которое образовано в результате вращения этой фигуры вокруг прямой, изображенной пунктиром.
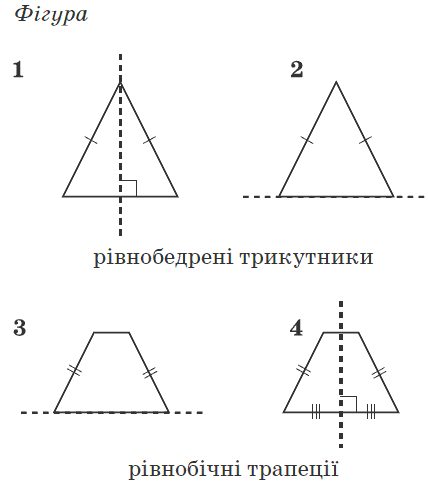
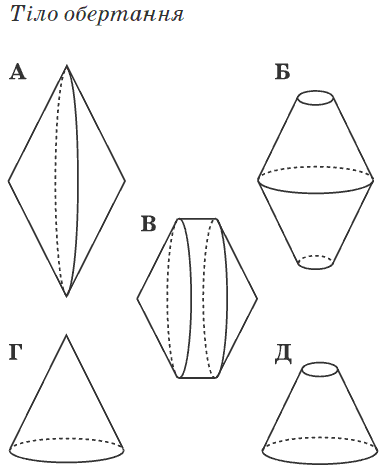
Решение : Задача не слишком сложная но лучше ее удается выполнить школьникам с хорошо развитым пространственным воображением. Для получения тела вращения можно выполнить рисунки в которых из удаленных от оси точек построить эллипсы большие оси которых равны расстояния до оси вращения. Также эти точки симметрично отобразить относительно оси и соединить линиями. В результате получим объемный вид фигур вращения.
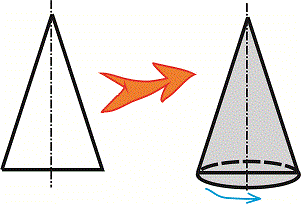
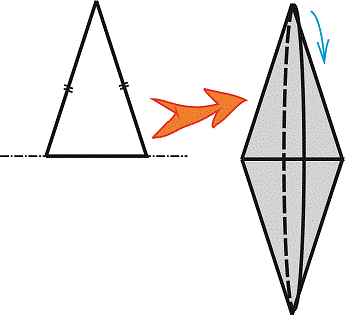
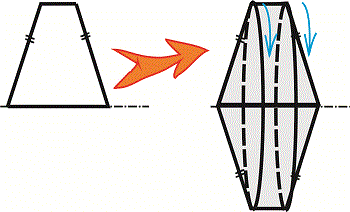
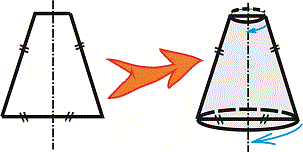
Наклоним некоторые графики на 90 градусов и приравняем к вариантам ответов.
Ответ: Без труда находим что фигуре 1 соответствует объемный вид А), 2 – Г), 3 – Д), 4 – В).
------------------------------
Посмотрите решение задач № 10-15 ВНО математика та решение задач № 22-27 ВНО математика
