Для нахождения моды и медианы случайной величины необходимы хорошие умения интегрировать и знания следующего теоретического материала. Модой 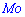 дискретной случайной величины
дискретной случайной величины 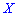 называют те ее возможное значение, которые соответствует наибольшей вероятности появления (т.е. такое значение величины
называют те ее возможное значение, которые соответствует наибольшей вероятности появления (т.е. такое значение величины 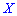 , которое случается чаще всего при проведении экспериментов, опытов, наблюдений). В случае случайной величины модой называют то ее возможное значение, которому соответствует максимальное значение плотности вероятностей
, которое случается чаще всего при проведении экспериментов, опытов, наблюдений). В случае случайной величины модой называют то ее возможное значение, которому соответствует максимальное значение плотности вероятностей
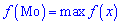
В зависимости от вида функции 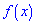 случайная величина
случайная величина 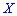 может иметь разное количество мод. Если случайная величина имеет одну моду, то такое распределение вероятностей называют одномодальным; если распределение имеет две моды — двухмодальным и более – мультимодальным.
может иметь разное количество мод. Если случайная величина имеет одну моду, то такое распределение вероятностей называют одномодальным; если распределение имеет две моды — двухмодальным и более – мультимодальным.
Существуют и такие распределения, которые не имеют моды, их называют антимодальными. Медианой  случайной величины
случайной величины 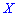 называют то ее значения, для которого выполняются равенство вероятностей событий, то есть, плотность вероятностей справа и слева одинаковы и равны половине (0,5)
называют то ее значения, для которого выполняются равенство вероятностей событий, то есть, плотность вероятностей справа и слева одинаковы и равны половине (0,5)
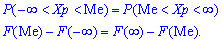
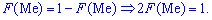
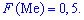
Графически мода и медиана изображенные на рисунке
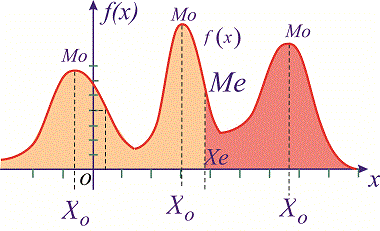
При таком значению случайной величины график функции распределения делится на части с одинаковой площадью. Непрерывная случайная величина имеет только одно значение медианы. Для дискретной случайной величины медиану обычно не определяют, однако в некоторой литературе приводятся правила, согласно которым, для ряда случайных величин размещенных в порядке возрастания (вариационного ряда) моду определяют распределения: если есть нечетное количество случайных величин 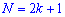 то медиана равна средней величине
то медиана равна средней величине
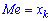
в случае четного количества 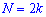 полусумме средних величин
полусумме средних величин
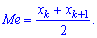
Рассмотрим примеры определения моды и медианы.
Пример 1. В развлекательном центре работник обслуживает четыре дорожки для боулинга. Вероятность того, что какая-то дорожка нуждается в уборке в течение смены является постоянной величиной с вероятностью 85%.
Построить закон распределения вероятностей дискретной случайной величины 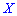 — количество дорожек, которые требуют уборки. Найти моду
— количество дорожек, которые требуют уборки. Найти моду 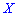 .
.
Решение. Случайной величина может принимать значения
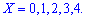
Вероятности появления значений определяем по образующей функцией
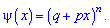
Для заданной задачи входные величины принимают значения
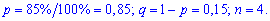
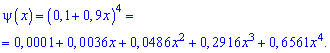
Искомые вероятности входят множителями при степенях аргумента
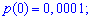
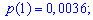
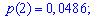
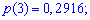
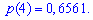
Закон распределения вероятностей запишем в виде таблицы
С таблице определяем моду 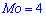 , как значение при максимальной вероятности. Получили одномодальное распределение
, как значение при максимальной вероятности. Получили одномодальное распределение
Пример 2. По заданной плотностью вероятностей
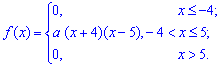
найти параметр  , плотность вероятностей
, плотность вероятностей 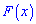 , моду
, моду 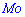 .
.
Решение. Применяя условие нормирования выполняем интегрирование
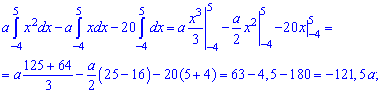
после того определяем параметр
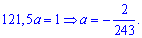
Плотность вероятностей, учитывая найденное значение будет иметь вид
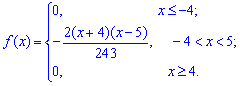
а ее график изображен на рисунке ниже
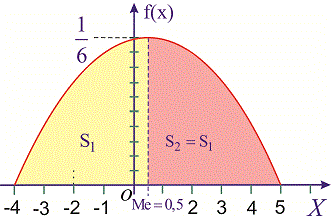
Из графика плотности вероятностей видим, что мода принимает значение 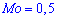 . Определим медиану
. Определим медиану  с помощью функции распределения вероятностей. Ее значение на промежутке
с помощью функции распределения вероятностей. Ее значение на промежутке 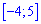 находим интегрированием
находим интегрированием
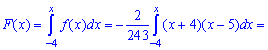
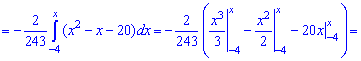
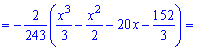
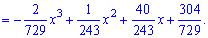
Функция распределения иметь следующий вид
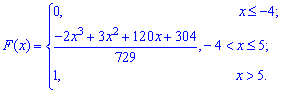
а ее график будет иметь вид
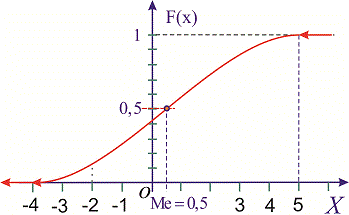
Для определения медианы случайной величины  применяем формулу
применяем формулу
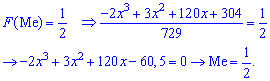
Медиану  можно найти с помощью плотности вероятностей
можно найти с помощью плотности вероятностей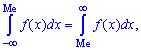
для дискретной случайной величины из промежутка 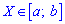
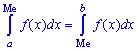
Таким образом медиану  — возможное значение случайной величины
— возможное значение случайной величины 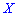 , при котором прямая, проведенная перпендикулярно соответствующей точки на плоскости
, при котором прямая, проведенная перпендикулярно соответствующей точки на плоскости 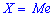 , делит площадь фигуры, ограниченной функцией плотности вероятностей
, делит площадь фигуры, ограниченной функцией плотности вероятностей 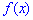 на две равные части.
на две равные части.
-------------------------------
Задача на определение моды и медианы случайной величины встречаются на практике не так часто, как плотности распределения вероятностей, однако вышеприведенный теоретический материал и решения распространенных примеров помогут Вам находить эти величины без больших затрат времени. При необходимости Вы всегда можете заказать решение задач по теории вероятностей в нас.


