Комбинаторика является важным разделом математики, который исследует закономерности расположения, упорядочения, выбора и распределения элементов с фиксированного множества.
При большом числе возможных последствий испытания способы прямого перебора возможных вариантов малоэффективны. На помощь приходят комбинаторные методы, в основе которых лежат два следующих правила.
ПРАВИЛО СУММИРОВАНИЯ
Если два взаимоисключающие действия могут быть выполнены в соответствии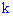 
и 
способами, тогда какое-то одно из этих действий можно выполнить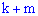 
способами.
Пример 1. Из города А в город В можно добраться 12 поездами, 3 самолетами, 23 автобусами. Сколькими способами можно добраться из города А в город В?
Решение. Проезд из А в В на поезде, самолете или автобусе являются событиями, которые не могут выполняться одновременно одним человеком (взаимоисключающими), поэтому общее количество маршрутов можно вычислить суммированием способов передвижения
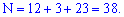
ПРАВИЛО ПРОИЗВЕДЕНИЯ
Пусть две выполняемые одно за другим действия могут быть осуществлены в соответстви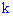и и способами. Тогда обе они могут быть выполнены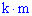 
способами.
----------------------------
Пример 2. В турнире принимают участие 8 хоккейных команд. Сколько существует способов распределить первое, второе и третье места?
Решение. Первое место займет одна из 8 команд, второе - одна из 7, третье - одна из 6, так как каждая из них не может претендовать одновременно на два призовых места. Поэтому таких способов будет ровно
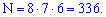
Оба правила обобщаются на случай любого конечного количества действий. В комбинаторике различают три вида различных соединений (комбинаций) элементов фиксированной множества: перестановки, размещения, сочетания. Ниже будут даны их определения с обозначениями, которые наиболее употребительные
Перестановками из из элементов называются такие их совокупности, отличающихся друг от друга только порядком вхождения элементов. Их обозначают 
и определяют по формуле
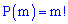
- факториал числа , определяется по правилу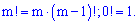 
----------------------------
Пример 3. Сколькими способами можно в детсадку поставить группу из 15 детей в ряд?
Решение. На первое место есть возможность поставить одного из 15 детей, на второе одного из 14 и т.д. Общее количество
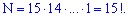
Размещением из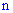 
элементов по называются такие совокупности элементов, отличающихся друг от друга по крайней мере одним элементом или порядком их вхождения (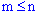
):
----------------------------
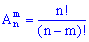
Пример 4. Сколько различных трехзначных чисел можно составить с помощью цифр от 1 до 9 ?
Решение. На первом месте есть возможность поставить одну из 9 цифр, на второе одного из 8 и т.д. Общее количество будет ровно
----------------------------
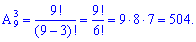
Сочетаниями из 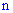элементов по называются такие комбинации из элементов, которые отличаются друг от друга по крайней мере одним элементом (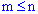
) :
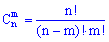
Пример 5. Сколькими способами можно выбрать три цифры из девяти 1, 2, 3, ..., 9?
Решение. Количество всех возможных способов определяем из формулы
----------------------------
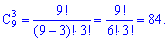
Приклад 6. Из одиннадцати букв азбуки составлено название украинской сказки «Котигорошок». Ребенок, не умеющий читать, рассыпал буквы, а затем собрал в произвольном порядке. Найти вероятность того, что он соберет слово «Котигорошок».
Решение. На здравый смысл получается, что такая вероятность равна нулю, однако это не так. Согласно теории, с одиннадцати букв можно составить различные буквосочетание, отличающиеся между собой только порядком букв, поэтому число всех возможных перестановок равно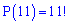 
Однако буквы «К» и «О» могут занимать одну из четырех, и одну из двух позиций соответственно, их можно переставлять. Поэтому число благоприятных событий равно
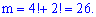
Искомая вероятность примет значение
----------------------------
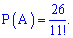
Хорошо разберитесь с приведенными примерами, которые показывают где применять на практике правило сложения, а где умножения; на их основе построен весь следующий материал. Впереди еще много нового следует изучить, здесь только основы теории вероятностей.
