Производные высших порядков. Правила и примеры

Под производной высших порядков понимают дифференцирования функции более одного раза. Если производнуюповторно дифференцировать, то получим производную второго порядка, или вторую производную функции , и она обозначается

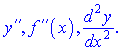
Производная третьего порядка будет иметь вид

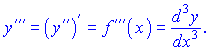
Аналогично получают формулы для нахождения производных высших порядков. При нахождении производной порядке необходимо иметь производную порядка. Исключение составляют функции для которых можно заметить тенденцию изменения производных. Это степенные, некоторые тригонометрические и экспоненциальные функции:

В других случаях, для нахождения производных высших порядков от заданной функции нужно последовательно находить все ее производные низших порядков. Для практического усвоения материала рассмотрим примеры.

Пример 1.

Вычислить производные второго порядка

1)

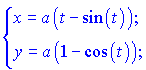
2)

3)

4)

Решение.

1) По правилам дифференцирования параметрических функций имеем

Применим к заданной функции. Найдем производную

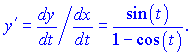
Дифференцируем второй раз. По правилу дифференцирования получим

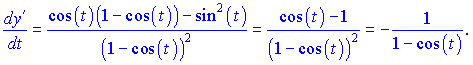
По формуле вычисляем

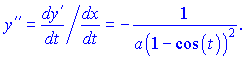
2)Определяем первую производную для функции

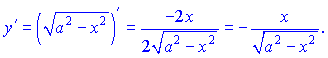
Вычисляем вторую производную

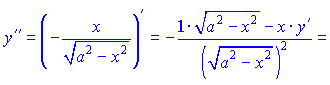
3)Вычислим первую производную

а потом вторую

При нахождении производной второго и высших порядков для данного примера и ему подобных можно пользоваться следующим правилам:

1) если степень функции меньше порядка производной , то она вклада не дает

2) все старшие степени дают вклад

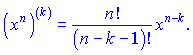
По такой схеме вторую производную можно было найти так:

Для практики второй способ эффективнее, особенно если нужно найти производные гораздо более высоких порядков чем второй.

4) Производную функции первого порядка будет иметь вид

второго порядка

По аналогии можно вывести формулу для производной экспоненциальной функции порядка

Решая примеры для синус и косинус функций можно заметить сходство при исчислении старших производных и вывести следующие зависимости

Пользуйтесь и пусть не возникают проблемы с производными высших порядков.