На предыдущем уроке из курса ВНО подготовки Вы познакомились с формулой раскрытия логарифмов
logaf(x)=c⇔f(x)=ac.
{x>0, x≠1, f(x)>0}
и ее частичными случаями:
логарифм основания равен единице
c=1⇔logaa=1⇔f(x)=a.
логарифм единицы равен нулю
c=1⇔loga1=0⇔f(x)=1.
Мы настолько часто пользуемся этими свойствами логарифмов, что после прочтения всех примеров Вы точно будете знать, где и для чего нужны эти формулы.
Примеры раскрытия логарифмических уравнений
Курс подготовки ВНО состоит из 40 примеров от простых до сложных, так что по номеру примера Вы можете следить, какой класс задач решается. По мере углубления Вы будете знакомиться с новыми формулами и свойствами логарифмов, без которых уравнение невозможно решить.
Пример 16.7 Решить уравнение log2(x+1)-log2(x-1)=1 и указать промежуток, которому принадлежит его корень.
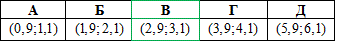
Решение: Выписываем ОДЗ:
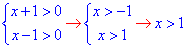
По правилу, разницу логарифмов выражений заменяем логарифмом частки + логарифм основания равен единице, в результате опускаем логарифмы и приравниваем выражения:
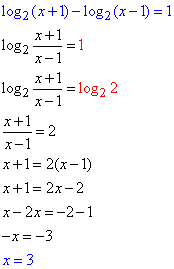
x=3 – корень заданного уравнения, принадлежащий промежутку (2,9;3,1).
Ответ: (2,9;3,1) – В.
Пример 16.8 Решить уравнение log2(x+1)+log(x+2)=3-log24 и указать промежуток, которому принадлежит его корень.
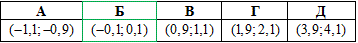
Решение: Составим систему неравенств для ОДЗ:
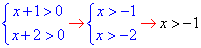
Используя ряд свойств логарифма, сводим уравнение к одному основанию, и раскрываем его.
Далее раскладываем неполное квадратное уравнение на простые множители
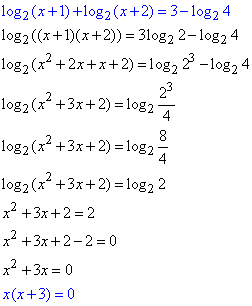
x1=0
x2=-3<-1 (не принадлежит ОДЗ).
x=0 – единственный корень заданного уравнения с интервала (-0,1;0,1).
Ответ: (-0,1;0,1) – Б.
Пример 16.10 Указать уравнение, равносильное уравнению
log3x-log9x+log81x=7.
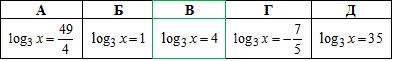
Решение: ОДЗ: x>0
Вынесем степени из основания логарифмов и сгруппируем
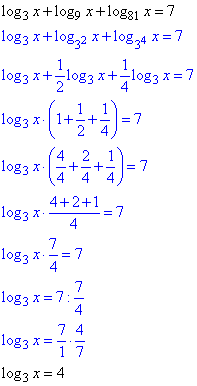
Уравнение log3x=4 и есть равносильное заданному.
(его решение x=3^4=81).
Ответ: log3x=4 – У.
Пример 16.11 Указать уравнение, равносильное уравнению x^lg(x)=10.
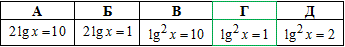
Решение: ОДЗ: {x>0, x≠1}.
Прологарифмируем обе части показательного уравнения
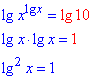
Конечное уравнение и является искомым равносильным уравнением.
(x1=10 или x2=0,1).
Ответ: lg2x=1 – Г.
Пример 16.12 Указать уравнение, которое получается из уравнения x^lg(x)=1000x^2 в результате логарифмирования обеих его частей.
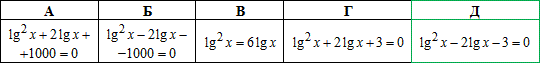
Решение: ОДЗ: {x>0, x≠1}.
Прологарифмируем обе части уравнения по основанию 10.
При этом помните, что десятичный логарифм 10 равен 1
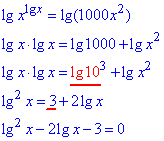
таким образом нашли уравнение, которое равносильно начальному.
(x1=1000 или x2=0,1).
Ответ: lg2(x)-2•lg(x)-3=0 – Д.
Пример 16.13 Указать уравнение, равносильное уравнению 2lgx2-lg2(-x)=4.
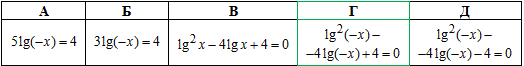
Решение: ОДЗ: -x>0, x<0.
Вынесем из под логарифма степень =2 и перегруппируем слагаемые
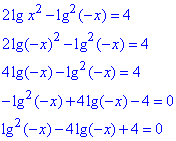
Это и есть все манипуляции, чтобы найти уравнение, которое равносильно заданному
2lgx2-lg2(-x)=4.
С помощью других преобразований Вы бы его не получили.
(x=-100).
Ответ: lg2(-x)-4•lg(-x)+4=0 – Г.
Пример 16.14 Решить уравнения
logalogblogcx=0.
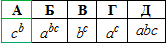
Решение: ОДЗ: x>0.
Имеем три вложенные логарифмы, поэтому по свойствам добиваемся равных основ логарифмов справа и слева от знака равенства, и раскрываем уравнение за схемой
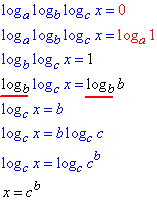
Такого плана задания в свое время были популярны на олимпиадах.
Ответ: cb – А.
Пример 16.15 Указать количество корней уравнения
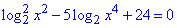
А | Б | В | Г | Д |
Четыре | три | два | один | ни одного |
Решение: ОДЗ: x≠0.
Путем введения замены переменных уравнение сводим к квадратному, после вычисления которого решаем 2 простых логарифмических уравнения.
Подробные объяснения хода преобразований приведены в таблице

Все найденные значения (-8; -4; 4; 8) принадлежат ОДЗ, уравнение имеет четыре решения.
Ответ: Четыре – А.
Пример 16.24 Установить соответствие между уравнениями (1-4) и произведениями их корней (А–Д).
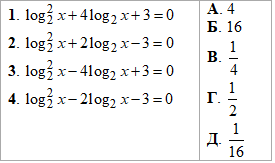
Решение: Все 4 варианта логарифмических уравнений сводим путем замены переменных к квадратным, после нахождения корней последних возвращаемся к замене и вычисляем простые уравнения с логарифмами. Так как в ответе нужно найти произведение корней, то условие ОДЗ допускает все значения.
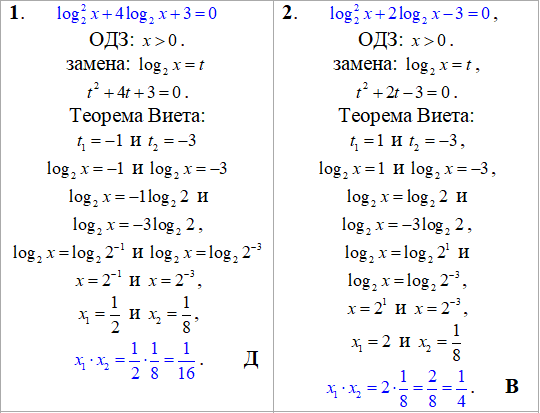

Решение уравнений с логарифмами невозможно без знания их свойств. Обращайте внимание на подчеркивания в формулах, они даются не просто так, эти две формулы к концу занятий Вы должны выучить на память и поверьте, что у Вас это получится.
А сейчас переходите к новым готовым ответам с ВНО подготовки на логарифмические уравнения.


