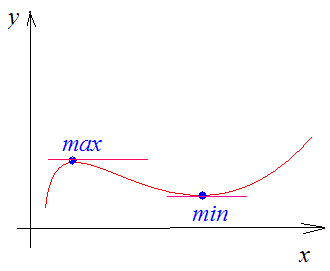
Критические точки – это точки в которых производная функции равна нулю или не существует. Если производная равна 0 то функция в этой точке принимает локальный минимум или максимум. На графике в таких точках функция имеет горизонтальную асимптоту, то есть касательная параллельна оси Ох.
Такие точки называют стационарными. Если видите на графике непрерывной функции «горб» или «яму» помните, что максимум или минимум достигается в критической точке. Рассмотрим для примера следующее задание.
Пример 1. Найти критические точки функции y=2x^3-3x^2+5 .
Решение. Алгоритм нахождения критических точек следующий:
- Находим производную функции
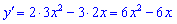
- Из условия равенства нулю производной определяем критические точки функции
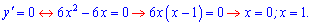
Итак функция имеет две критические точки.
Далее, если нужно провести исследование функции то определяем знак производной слева и справа от критической точки. Если производная при переходе через критическую точку меняет знак с «-» на «+», то функция принимает локальный минимум. Если с «+» на «-» должны локальный максимум.
Второй тип критических точек это нули знаменателя дробных и иррациональных функций
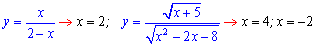
Функции с логарифмами и тригонометрические, которые не определены в этих точках
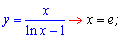
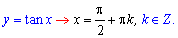
Третий тип критических точек имеют кусочно-непрерывные функции и модули.
Например любая модуль-функция имеет минимум или максимум в точке излома.
Например модуль y = | x -5 | в точке x = 5 имеет минимум (критическую точку).
Производная в ней не существует, а справа и слева принимает значение 1 и -1 соответственно.
Попробуйте определить критические точки функций
1) 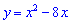
2) 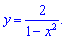
3) 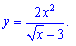
4) 
5) 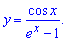
Если в ответе у Вы получите значение
1) x=4;
2) x=-1;x=1;
3) x=9;
4) x=Pi*k;
5) x=1.
то Вы уже знаете как найти критические точки и сможете справиться с простой контрольной или тестами.