Максимумом (минимумом) функции двух переменных по определению, это как и для функции f(x) одной переменной максимальное (минимальное) ее значение. На плоскости это "холмы" и "ямы", в пространстве - то же только имеет двумерное изображение. Представить как правило всегда легко, а вот для заданной функции найти точки экстремума может не каждый.
Схема исследования функции двух переменных на экстремум
Первое что нужно - это проверить выполняются ли необходимые условия экстремума, а они следующие - если функция имеет частные производные первого порядка и они равны нулю то в этих точках функция может иметь экстремумы. На практике реализация теории следующая: вычисляем частные производные и приравниваем их к нулю. В результате получим систему уравнений
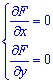
из которой нужно найти точки (x0; y0) подозрительные на экстремум, их еще называют стационарными.
Чтобы установить имеет ли место максимум функции, или минимум нужно вычислить частные производные второго порядка (A, B, C) в критических точках
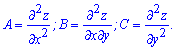
Далее в найденных точках нужно найти параметр дифференциала D
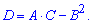
Далее возможны 4 случая:
- функция имеет максимум, если A<0; D>0
- функция имеет минимум, если A>0; D>0
- не имеет экстремума, если D<0
- при D=0 нужно проводить дополнительный анализ на экстремум.
Из анализа знаков A, D и делают выводы о точках максимума и минимума функции. Далее подстановкой точек вычисляют сам экстремум функции.
Если надо найти наибольшее (наименьшее) значение функции в замкнутой области (треугольник, прямоугольник, круг), то эти кривые подставляем в исходное уравнение и исследуем функцию на экстремум по линиям, а также проверяем стационарная точки (если они принадлежит замкнутой области). Такой пример рассмотрен в готовых контрольных работах.
Примеры на экстремумы
Пример 1. Найти экстремум функции двух переменных
Z=2*x*y-3*x^2-2*y^2
Решение: Чтобы найти критические точки функции двух переменных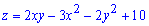 
для начала нам следует вычислить частные производные первого порядка
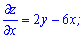
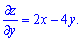
Далее приравниваем частные производные к нулю и решаем систему уравнений
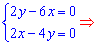
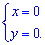
Найденные значения и являются координатами критической точки. Чтобы не исследовать функцию в окрестности точки экстремума, поскольку не имеем графика функции, установим знаки вторых частных производных в точке. Вычисляем производную второго порядка в критической точке (0;0)
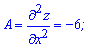
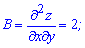
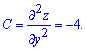
Далее вычисляем параметр D
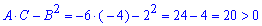
Знак A<0, D>0 больше нуля, так что в критической точке (0, 0) функция имеет максимум. Значение равно свободном члену
График пространственной функции в окрестности точки экстремума имеет вид
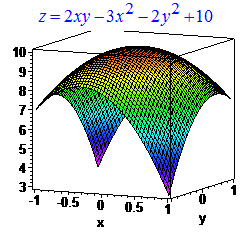Пример 2. Найти точку максимума или минимума заданной функции
Z=4*x-6*y-x^2-3*y^2+5
Решение: По стандартной схеме ищем производные первого порядка
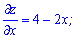
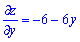
и приравниваем их к нулю. В результате получим систему уравнений с которой находим критическую точку функции
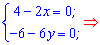
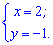
Найденая точка экстремума имеет координаты (2; -1).
Чтобы установить имеет ли место минимум функции или максимум найдем частные производные второго порядка
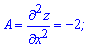
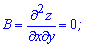
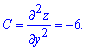
Находим параметр
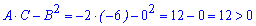
Он положительный, так что в найденной точке функция достигает максимума. Вычислим его значение подстановкой
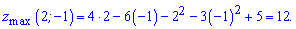
Точка максимума на графике будет выглядеть следующим образом
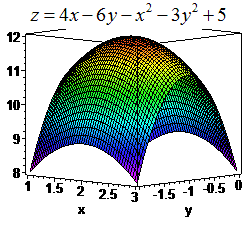Пример 3. Исследовать функцию двух переменных на экстремум
Z=3*x^2-x*y+y^2-7*x-8*y+2
Решение: Вычисляем частные производные первого порядка функции
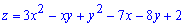
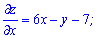
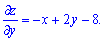
Приравниваем производные к нулю и решаем систему уравнений
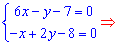
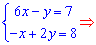
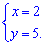
Критическая точка имеет координаты (2, 5). Для выяснения характера точки экстремума найдем производные второго порядка в критической точке
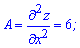
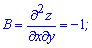
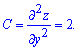
Вычисляем параметр D
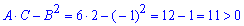
Знак A, D положительный, значит в точке (2; 5) данная функция имеет минимум, вычисляем минимальное значение
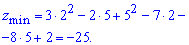
График функции двух переменных приведен ниже
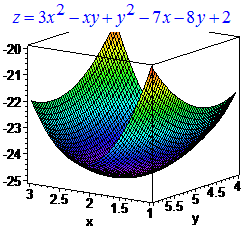Пример 4. Найти экстремум функции двух переменных
Z=2*x^2-3*y^2+4*x+6*y+5
Решение: Найдем критические точки функции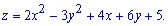 
Вычисляем частные производные
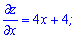
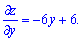
и приравниваем их к нулю. В результате получим систему уравнений для нахождения точки экстремума
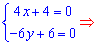
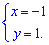
Найдем производную второго порядка в стационарной точке (-1; 1)
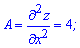
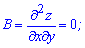
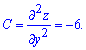
Вычисляем параметр D
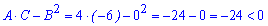
Знаки A>0,D<0, так что в точке (-1; 1) функция не имеет экстремума. Это точка перегиба пространственной функции. На графике это выглядит так
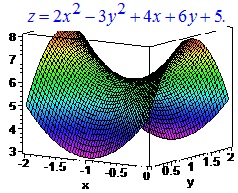Пример 5. Исследовать функцию на экстремум
Z=x^3+y^3-15*x*y+120.
Решение: Повторяем все пункты методики нахождения экстремумов.
Вычисляем частные производные функции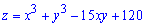 
первого порядка
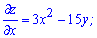
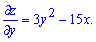
Приравниваем их к нулю и решаем
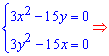
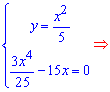
Отсюда получаем две подозрительные на экстремум точки
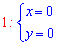
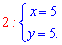
Далее находим производные второго порядка в критических точках (0; 0) и (5; 5)
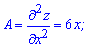
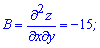
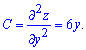
Характер первой критической точки:
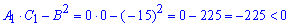
В точке (0; 0)данная функция не имеет ни максимума, ни минимума.
Характер второй критической точки:
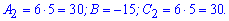
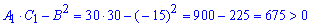
По признакам экстремума данная функция имеет минимум, а именно
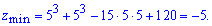
Анализ функции двух переменных в Мейпл
Приведем алгоритмы анализа функции и построения графиков в математическом пакете Maple. Фрагмент кода несколько проще чем вычисления вручную. Сначала нужно занулить все переменные и подключить библиотеку для построения 3D графиков
>restart;with(plots):
Далее вводим уравнения пространственной функции
> Z=x^3+y^3-15*x*y+120;
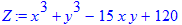Вычисляем частные производные
> diff(Z,x)=0;diff(Z,y)=0;
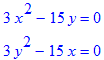Вторые производные можно найти повторным дифференцированием
> A:=diff(Z,x,x);C:=diff(Z,y,y);B:=diff(Z,x,y);
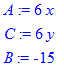Находим решения системы ривянянь командой solve
> solve({diff(Z,x)=0,diff(Z,y)=0},{x,y});
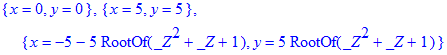Далее строим графики функции с помощью команды plot3d(F,x=a..b,y=c..d) . Здесь все обозначения должны быть Вам понятны
> plot3d(Z, x= -1..1, y=-1..1);
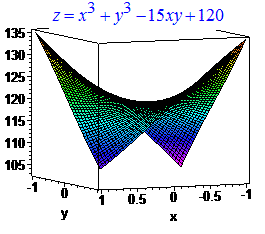> plot3d(Z, x= 4..6, y=4..6);
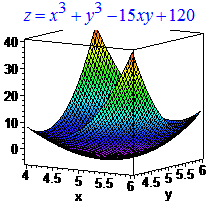В Мейпл нет необходимости анализировать другие производные, поскольку можем построить график и визуально проверить имеем максимум или минимум, а возможно и перегибы, как в последнем примере. Скачать математический пакет Maple Вы можете с официального сайта или поискать установочный пакет в сети интернет. Примеры приведены в пакете Maple 17.
Подобно приведенному выше выглядит анализ на экстремумы если заданные другие функции - тригонометрические, показательные, ... Все сводится к уравнениям на производные и вычислениям, которые Вы часто выполняете на занятиях.
Если не можете выполнить анализ на экстремум самостоятельно, тогда заказывайте решения задач, контрольных у нас!
