Формула Остроградського-Гаусса. Поток векторного поля

Формула Остроградського-Гаусса имеет широкое приложение в математике, физике, химии.
Дальше будут приведенные ответы к примерам по интегрированию, которые предусматривают нахождение потока векторного поля через дивергенцию.
В большинстве заданий вычисления двойных интегралов предусматривает замену переменных, а точнее - переход к полярной системе координат. Это упрощает подынтегральные выражения, однако ведет к пересчету пределов интегрирование.
На словах это легко понять, однако на практике необходимо анализировать приведенные примеры на формулу Остроградського-Гаусса и много решать самостоятельно, чтобы разобраться в теме.

Пример 7.1 Найти поток векторного поля 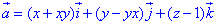через часть поверхности S:
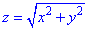, что отсекается плоскостью P:
z=2 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Уравнение 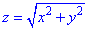- коническая поверхность с вершиной в точке (0;0;0), которая вытянута вдоль оси Oz.
z=2 - плоскость параллельная к плоскости Oxy. (шапка).
Приведены поверхность и плоскость изобразим в пространстве

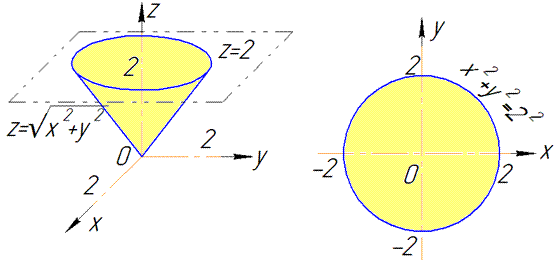
В сечении с конусом получим круг радиуса R=2.
Как видим из рисунка, четверть области V задается следующими пределами:

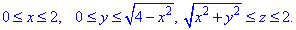
Здесь учли четность всех функций, поєтому результат интегрирования умножим на 4.
Вычислим дивергенцию векторного поля :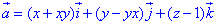

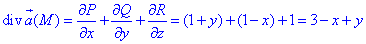
где P=P(x;y;z)=x+xy, Q=Q(x;y;z)=y-yx, R=R(x;y;z)=z-1.
Последние функции берем из a.
Найдем поток векторного поля за формулой Остроградського-Гаусса: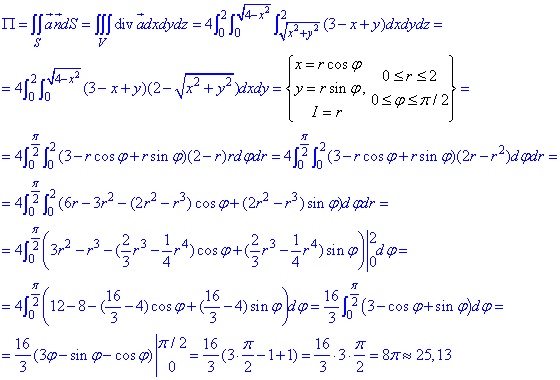

Пример 7.3 Найти поток векторного поля 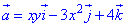через часть поверхности S:

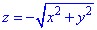, что отсекается плоскостью P:
z=-1 (нормаль внешня к замкнутой поверхности, образованной данным сечением).
Решение: 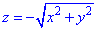- коническая поверхность (нижняя часть) с вершиной в начале координат (0;0;0), которая вытянута вдоль оси Oz.
z=-1 - плоскость параллельная к Oxy.

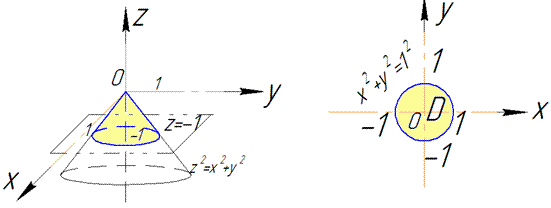
В сечении с конусом получим круг радиуса R=1.
Как видим из рисунка четверть области V задается следующими пределами:

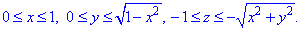
Здесь учли четность всех функций, поэтому результат интегрирования будем умножать на 4.
Находим дивергенцию векторного поля :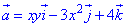

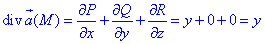
где P=P(x;y;z)=xy, Q=Q(x;y;z)=-3x², R=R(x;y;z)=4.
За формулой Остроградського-Гаусса вычисляем тройной интеграл:

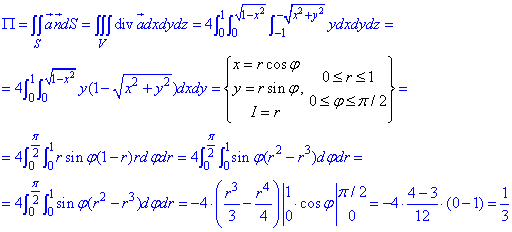
Переход к полярной системе координат значительно упрощает нахождения двойного интегралу.

Пример 7.4 Вычислить поток векторного поля 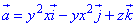через часть поверхности S: 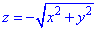, что вырезается плоскостью P:
z=-5 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Уравнение 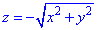- задает коническую поверхность с вершиной в точке(0;0;0), которая вытянута вдоль оси Oz.
z=-5 - плоскость параллельная к плоскости Oxy.

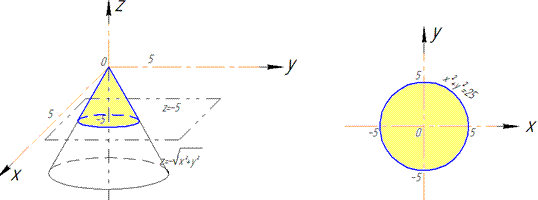
В сечении с конусом получим круг радиуса R=1.
Из рисунка следует что четверть области V задается следующими пределами:

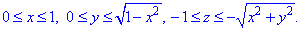
Здесь учитываем четность функций, поэтому результат будем множить на 4.
Находим дивергенцию векторного поля :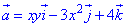

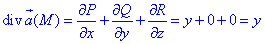
где P=P(x;y;z)=xy, Q=Q(x;y;z)=-3x², R=R(x;y;z)=4.
За формулой Остроградського-Гаусса вычисляем поток поля :

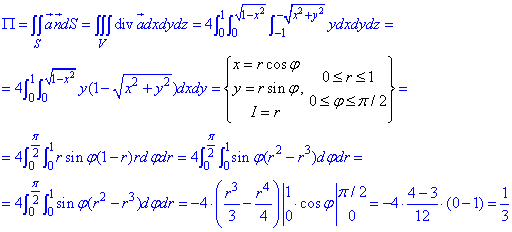
Переход к полярной системе координат значительно упрощает нахождения двойного интегралу.

Пример 7.5 Вычислить поток векторного поля 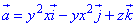через часть поверхности S:
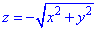, что вырезается плоскостью P:
z=-5 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Уравнение 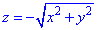- задает коническую поверхность с вершиной (0;0;0), которая вытянута вдоль оси Oz.
z=-5 - плоскость, какая параллельная к плоскости Oxy.

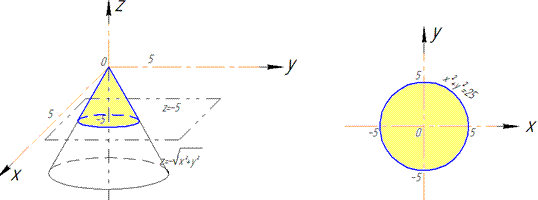
В сечении с конусом получим круг радиуса R=5.
Как видим из рисунка четверть области V задается следующими пределами: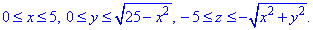
Принимая во внимание четность всех функций, можем сузить область интегрирования, а результат умножить на 4.
Дивергенция векторного поля 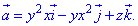равна

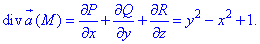
где P=P(x;y;z)=y²x, Q=Q(x;y;z)=-yx², R=R(x;y;z)=z.
Поток поля находим переходом к двойному интегралу по формуле: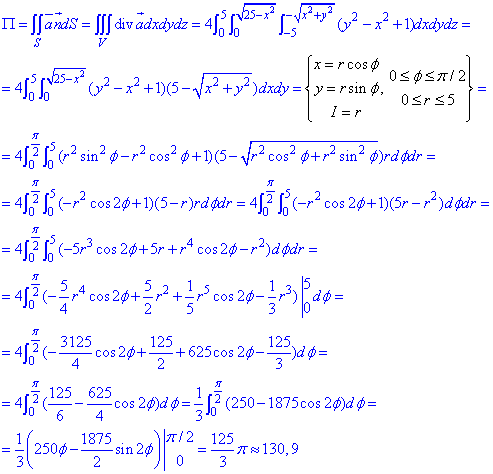

Опять имеем замену переменных под интегралом. Этот прием является незаменимым при нахождении интегралов по поверхностям вращения - подынтегральные функции и пределы упрощаются, отпадает потребность бороться с корнями и выискивать экзотические формулы интегралов из справочников.

Пример 7.7 Найти поток векторного поля 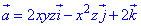через часть поверхности S:
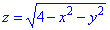, что отсекается плоскостью P:
z=0 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Сведем поверхность 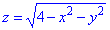к каноническому виду z²=4-x²-y², x²+y²+z²=2²- сфера (верхняя половина) с центром в (0;0;0) и радиусом R=2.
z=0 - плоскость параллельная к плоскости Oxy.

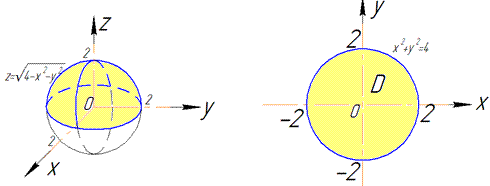
В сечении со сферой получим круг с центром в (0;0;0) и радиусом R=2.
Из рисунку видим четверть области V задается следующими пределами:

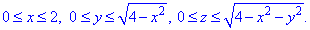
Здесь учли четность всех функций поэтому результат будем множить на 2.
Вычисляем дивергенцию :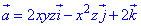

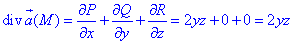
где P=P(x;y;z)=2xyz, Q=Q(x;y;z)=-x²z, R=R(x;y;z)=2.
Поток векторного поля определяем через формулу Остроградського-Гаусса:

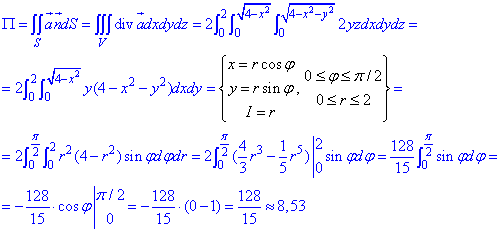
Пример 7.8 Найти поток векторного поля 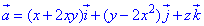через часть поверхности S:
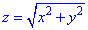, что вырезается плоскостью P:
z=4 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Уравнение 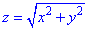описывает коническую поверхность с вершиной в начале координат (0;0;0), вытянутую вдоль оси Oz.
Сечение z=4 - плоскость параллельная к плоскости Oxy.

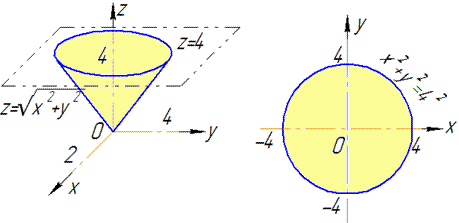
В сечении с конусом получим круг радиуса R=4.
Как видим из рисунка, четверть области V задается следующими пределами:

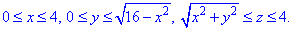
Четность всех функций позволяет искать интеграл на меньшей поверхности, затем результат нужно будет умножить на 4.
Дивергенцию векторного поля 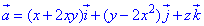определяем по формуле:

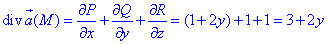
где P=P(x;y;z)=x+2xy, Q=Q(x;y;z)=y-2x², R=R(x;y;z)=z.
Интегрированием вычисли поток векторного поля :

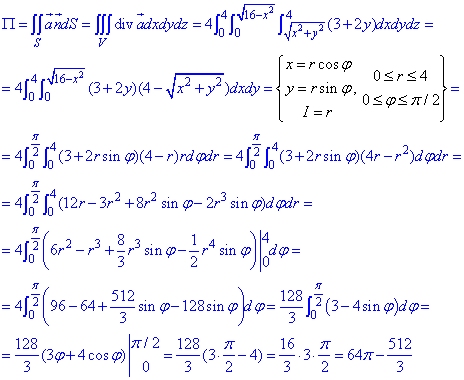
Пример 7.14 Определить поток векторного поля 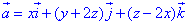через часть поверхности S:
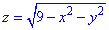, что отсекается плоскостью P:
z=0 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Уравнение 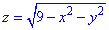- описывает верхнюю часть полусферы с центром в (0;0;0) и радиусом R=3.
В сечении с плоскостью z=0 получим круг радиуса R=3.

Четверть области V задается следующими пределами: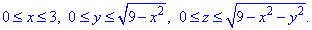

Принятие во внимание четности функций позволяет записать пределы лишь в четверти области, потому поток необходимо умножить на 4.
Посчитаем дивергенцию поля :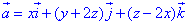

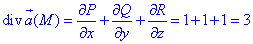
где P=P(x;y;z)=x, Q=Q(x;y;z)=y+2z, R=R(x;y;z)=z-2x.
Применяем формулу Остроградського-Гаусса для определения потока векторного поля :

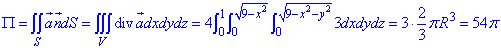
Пример 7.15 Найти поток векторного поля 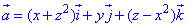через часть поверхности S:
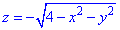, что пересекается плоскостью P:
z=0 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Поверхность 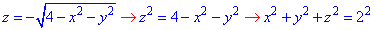- сфера (нижняя часть) с центром в начале декартовой СК (0;0;0) и радиусом R=2.

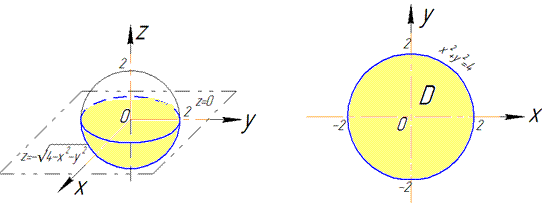
В сечении плоскости z=0 со сферой получим круг радиуса R=2.
Четверть области V задается следующими пределам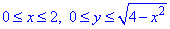и:
и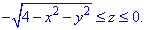
Результат интегрирования необходимо умножить на 4, поскольку учитываем четность функций.
Вычислим дивергенцию векторного поля :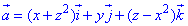

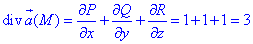
где функции P=P(x;y;z)=x+z², Q=Q(x;y;z)=-y, R=R(x;y;z)=z-x².
Интегрированием находим поток векторного поля :

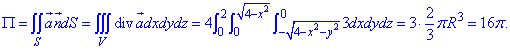
Он равен P=16pi.

Пример 7.16 Найти поток векторного поля 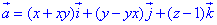через часть поверхности S:
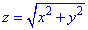, что отсекается плоскостью P:
z=2 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Корневая зависимость 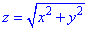- задает коническую поверхность с вершиной в точке (0;0;0), которая вытянута вдоль оси Oz.
z=2 - плоскость параллельная к плоскости Oxy.
В сечении с конусом получим круг радиусом R=2.

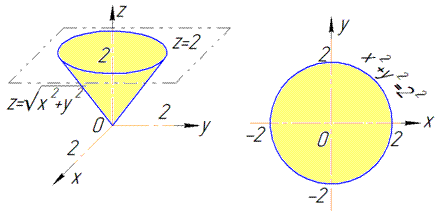
Четверть области V задается следующими пределами: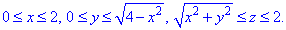

Четность функций учтена, поэтому результирующий интеграл нужно умножить на четверку.
Вычислим дивергенцию векторного поля :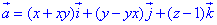

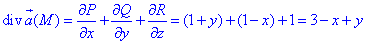
где P=P(x;y;z)=x+xy, Q=Q(x;y;z)=y-yx, R=R(x;y;z)=z-1.
За формулой Остроградського-Гаусса вычисляем поток векторного поля :
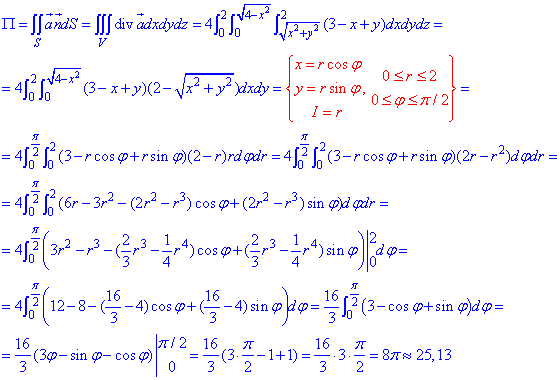Алгоритм вычисления двойных интегралов из примера в пример не изменяется.
Переход к полярной системе координат при интегрировании Вы должны хорошо знать, такой прием позволяет упростить широкий класс интегралов, а дальнейшие вычисления свести к простым интегралам от показательных  и тригонометрических функций. В отдельных случаях Вам придется применять формулы понижение степеней для перехода от квадратов синусов и косинусов к их первым степеням.

Пример 7.24 Вычислить поток векторного поля 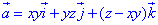через часть поверхности S:
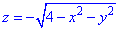, что отсекается плоскостью P:
z=-1 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Превращаем уравнение поверхности 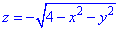к каноническому виду
z^2=4-x^2-y^2, x^2+y^2+z^2=2^2 - сфера (нижняя часть) с центром в начале координат (0;0;0) и радиусом R=2.
z=-1 - плоскость параллельная к плоскости Oxy.

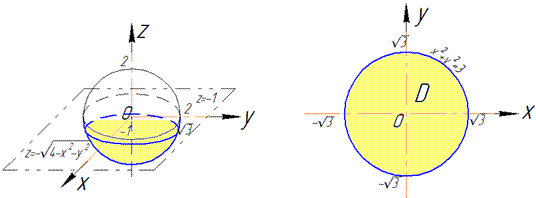
В сечении со сферой получим круг радиусом корень из трех
Четверть области V задается следующими пределами: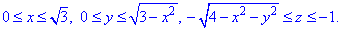

В силу четности функций, выписываем пределы лишь на 1/4 поверхности сферы.
Дивергенция векторного поля 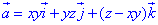через частичные производные равна:

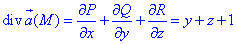
где функции P=P(x;y;z)=xy, Q=Q(x;y;z)=yz, R=R(x;y;z)=z-xy.
Поток векторного поля определяем из двойного интеграла:

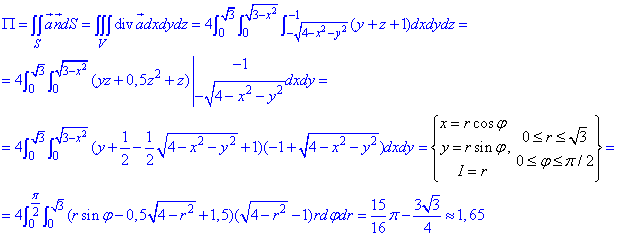
На этом ознакомление с примерами на вычисление потока векторного поля не завершается, больше готовых ответов Вы найдете на соседних страницах.