Шановні школярі, випускники, абітурієнти, цей розділ допоможе при підготовці до зовнішнього оцінювання 2017 року з математики. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень при підготовці до тестування, систематизувати та підвищити накопичений рівень знань з математики.
Розділ II. Рівняння і нерівності
Завдання 11.85 Знайдіть суму х + у, якщо пара (х;у) є розв'язком системи рівнянь
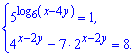
Розв'язання: Такий приклад системи рівнянь на ЗНО тестуванні з математики мало хто хотів би бачити у тестовому завданні. Першим стоїть показникове і логарифмічне рівняння в одному. Однак вихід є, на момент треба уявити , що логарифм це число. Якщо 5 піднести до степеня маємо дістати одиницю. Всі повинні знати, що таке можливо якщо показник рівний нулю, тобто праву сторону слід переписати у вигляді
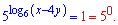
Далі починаються простіші обчислення, прирівнюємо показники при рівних основах і переходимо до розгляду логарифмічного рівняння
log6(x-4*y) =0.
Потенціюємо логарифм і отримаємо залежність між коренями
x-4*y=60,/=1;
x=4*y+1.
Показник в другому рівнянні з врахування знайденої залежності прийме вигляд
x-2*y=4*y+1-2*y=2*y+1.
Далі показникове рівняння заміною змінних
22*y+1=t
зводимо до квадратного рівняння
t2-7*t-8=0.
Дане рівняння можемо розкласти на прості множники
(t-8)(t+1)=0
або за теоремою Вієта підібрати корені t=8; t=-1. Другий корінь відкидаємо, оскільки повернувшись до заміни отримаємо, що показникові функція приймає від'ємне значення, а такого бути не може. Перший корінь дасть наступний вклад
22y+1=8=23;
2*y+1=3;
2*y=3-1=2;
y=2/2=1.
Другий розв'язок системи рівнянь обчислюємо з умови
x=4*y+1=5.
Згідно умови прикладу сумуємо знайдені корені
x+y=5+1=6.
Відповідь: 6.
Завдання 11.86 Знайдіть суму х0 + у0 для одержаного розв'язку (х0 ; у0) системи рівнянь
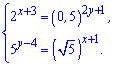
Розв'язання: Задано досить просту і зрозумілу систему показникових рівнянь. Все що потрібно для обчислень – перетворити праві сторони до однієї основи з лівими і прирівняти показники. В результаті система показникових рівнянь зведеться до системи лінійних рівнянь. Розпочнемо з перетворення правих сторін
2x+3=(1/2)2y+1;
52y-4=51/2(x+1).
Далі прирівнюємо показники
1 x+3=-1-2y;
2: x+1=2y-8.
Додамо до другого рівняння перше та обчислимо невідому
2*x+4=-9;
2*x=-9-4=13;
x=-13/2.
Знайдене значення підставимо в 1 із рівнянь СЛАР
2y=-1-3-x;
2y=-4-x=-4+(13/2)=-8/2+13/2=5/2;
y=5/2/2=5/4.
Обчислюємо суму коренів системи рівнянь
x+y=(5/4)-(15/2)=(5-30)/4=25/4=6,25.
Відповідь: 6,25.
Залишайтеся з нами і підготовка до ЗНО з математики залишиться для Вас приємним спогадом та зекономить багато часу та грошей на репетиторів.
Відповіді до ЗНО тестів
- ЗНО 2017 відповіді з математики
- Попередня стаття - ЗНО 2017 математика. Розв'язок логарифмічного рівняння
- Наступна стаття - ЗНО 2017 математика. Рівняння підвищеної складності


