Розв'язки задач з теорії ймовіростей шукає чимало студентів, та не усі з них залишаються задоволені відповідями до завдань та поясненнями. В цій статті Ви можете не тільки отримати розв'язки завдань з ймовірності, а й вивчити інструкції знаходження ймовірностей за відомими з теорії формулами. Приклади охоплюють широкий клас теоретичного матеріалу та дозволяють швидко встановити рівень знань практичного матеріалу у студентів.
ВАРІАНТ – 17
Завдання 1 Із урни, в якій 10 білих, 4 чорних та 5 синіх кульок, навмання вибирають три кульки. Знайти ймовірність того, що серед них будуть:
- а) всі білі;
- б) всі чорні;
- в) 1 біла, 1 синя, 1 чорна.
Розв'язання: На методиці вирішення таких задач зупинятися не будемо, нагадаємо лише, що кількість подій - сприятливих та можливих знаходимо через розміщення. Число всіх можливих подій за якими можна вибрати 3 кульки з 19 (10+4+5) рівне A193:
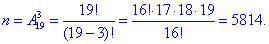
Формулу для факторіалів Ви повинні використовувати досить легко, оскільки майже всі формули теорії ймовірностей побудовані на факторіалах.
а) Число сприятливих подій за якими можна вибрати три білі кульки із 10 можливих рівна A103=720:
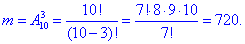
Ймовірність події A, при якій вибирають три кульки білого кольору знаходимо за класичною формулою рівна:
P(B)=m/n=720/5814=0,1238.
б) Кількість способів, за якими можна вибрати три чорні кульки із 4 можливих рівна A43: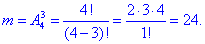 
Знаменник завжди той самий, оскіьки кількість можливих варіантів вибрати три кульки ми знайшли на початку. Далі через частку m/n обчислюємо ймовірність події B, при якій вибирають три кульки чорного кольору:
P(B)=m/n=24/5814=0,0041.
в) Цей пункт на пратиці багато студентів виконує неправильно. Число сприятливих подій за якими можна вибрати 1 білу кульку з 10, 1 чорну кульку з 4 і 1 синю кульку з 5 знаходимо через добуток розміщень:
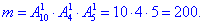
Ймовірність події C, при якій вибирають 1 білу, 1 чорну і 1 синю кульки рівна:
P(C)=m/n=200/5814=0,0344.
Якщо Ви читали відповіді до попередніх контрольних то мабуть зауважили, що є інший спосіб обчислити ймовірності.
Завдання 2 В продукції заводу брак складає 5% від загальної кількості деталей. Для контролю відібрано 20 деталей. Знайти ймовірність того, що серед відібраних
- а) одна бракована;
- б) не більше чотирьох бракованих;
- в) жодна не бракована.
Розв'язання: Ймовірність відбирання бракованих деталей змінюється за біноміальним законом, де n=20, p=0,05, q=1-p=0,95:
Формула розподілу ймовірностей має вигляд
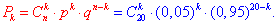
а) Ймовірність того, що серед відібраних одна бракована k=1:
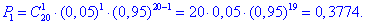
б) Ймовірність того, що серед відібраних не більше чотирьох бракованих – це означає або 0, або 1, або 2, або 3, або4 бракованих:
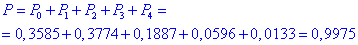
Умова "або" при обчисленні ймовірності виражається знаком додавання, а не множення. Це вивчіть і застосовуйте де потрібно.
в) Ймовірність того, що серед відібраних жодна не бракована означає 0 з 20: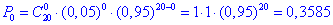 
Ось такими легкими можуть бути відповіді, якщо знаєте формули.
Завдання 3 На контроль надійшли вироби, які виготовлені трьома робітниками. Перший виготовив 30 виробів, серед яких 7% браку, другий – 50 виробів, серед яких 4% браку, а третій – 40, серед яких 3% браку. Взятий навмання виріб – доброякісний. Знайти ймовірність того, що виріб виготовив 2-й робітник.
Розв'язання: Ви повинні знати, що така задача розв'язується через формулу повної ймовірності та Байєса. Якщо не знаєте назви формул, то хоч запам'ятайте наступну методику.
Позначаємо через Hi - гіпотези, що виріб виготовлений і-м робітником, де i=1,2,3. Тоді ймовірність кожної з гіпотез рівна частці виробів в загальній сукупності:
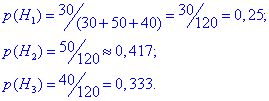
Їх сума повинна бути рівна повній ймовірності (1). Якщо не так, значить Ви або чогось не врахували або допустили помилку.
Далі подія A полягає в тому, що взятий навмання виріб доброякісний. На основі умови можемо виписати ймовірності того, що доброякісний виріб виготовив кожен із робітників:
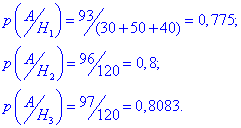
За формулою повної ймовірності знаходимо ймовірність, що виріб доброякісний:
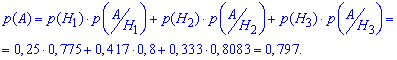
Це по суті сума вкладів кожного з робітників помножена на якість виробів.
Ймовірність того, що виріб виготовив 2-й робітник за формулою Байєса рівна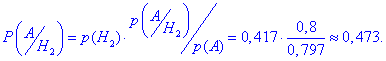 
Якщо проаналізувати попередню формулу, то це вклад другого доданку в знайдену ймовірність.
Завдання 4 Вважаючи, що ймовірність навчатися у ВУЗі для хлопців та дівчат рівна, знайти ймовірність того, що серед 300 студентів:
- а) 200 дівчат;
- б) не менше 100 і не більше 170 дівчат.
Розв'язання: а) Оскільки ймовірність навчатися у ВУЗі для дівчат і хлопців рівна p=0,5, то за формулою Бернуллі знаходимо точне значення
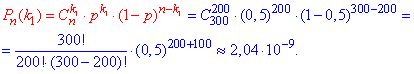
Без знання математичних програм таке значення знайти важо, інженерні калькулятори при високих показниках (300) дають похибку.
Єдиний можливий варіант - знайти наближене значення за локальною теоремою Лапласа.
Оскільки умова застосування формул виконується n*p*q=300*0,5*0,5=75>10, то похибка обчислень мінімальна
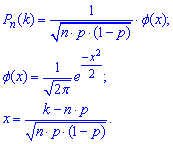Виконаємо обчислення аргумента функції Лапласа:
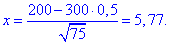
За таблицями табулювання локальної функції Лапласа маємо phi
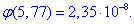
Підставляємо та знаходимо ймовірність
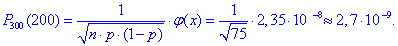
Зважаючи на показник степеня при основі 10, розбіжність зі значенням отриманим за формулою Бернуллі незначне!
б) Ймовірність, що не менше 100 і не більше 170 дівчат у ВУЗі знайдемо за інтегральною формулою Лапласа:
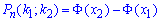де 
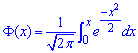- інтегральна функція Лапласа;
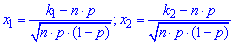- аргументи інтегральної функції розподілу.
Знайдемо дві точки
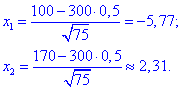
Далі значення інтегральної функції Лапласа в x1, x2 підставляємо в формулу ймовірності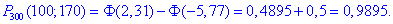 
Завдання 5 В партії 20% нестандартних деталей. Навмання вибрані чотири з них (n=4). X - число стандартних серед відібраних. Знайти закон розподілу випадкової величини X, знайти математичне сподівання випадкової величини M(X), дисперсію D(X), середньоквадратичне відхилення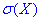 
, функцію розподілу F(X) та побудувати її графік.
Розв'язання: Умова "В партії 20% нестандартних деталей" означає, що від досліду до досліду ймовірність залишається сталою, а саме p=0,8 і q=1-p=0,2.
Таким чином ймовірність відбирання стандартних деталей змінюється за біноміальним законом:
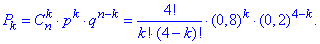
Результати розрахунків запишемо в таблицю розподілу ймовірностей:
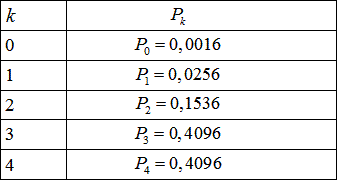Будуємо графік закону розподілу (щіьності)
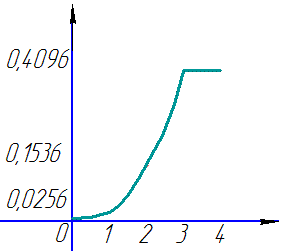Математичне сподівання випадкової величини рівне
M(X)=n*p=4*0,8=3,2.
Дисперсію знаходимо за формулою
D(X)=n*p*q= 4*0,8*0,2=0,64.
Через корінь квадратний з дисперсії визначаємо середнє квадратичне відхилення випадкової величини X:
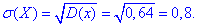
Функцію розподілу випадкової величини X знаходимо за формулою:
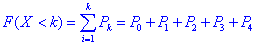
Результати обчислень записуємо у таблицю:
За знайденими значеннями будуємо графік функції розподілу ймовірностей
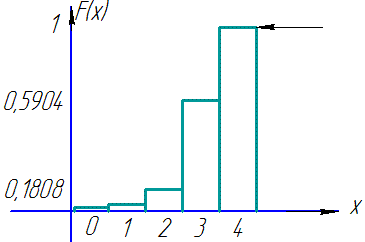На цьому приклад розв'язано.
Завдання 6 Випадкова величина задана щільністю розподілу f(x):
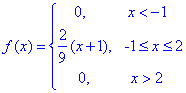Знайти функцію розподілу F(X), математичне сподівання випадкової величини M(X), дисперсію D(X) випадкової величини та ймовірність того, що в результаті випробувань x набуде значень, що належать інтервалу (a;b). Побудувати графіки f(x) та F(x).
Розв'язання: Функція розподілу обчислюємо інтегруванням f(x):
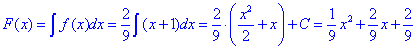
В результаті отримаємо сталу справа, яку довизначаємо умовою F(b)=1:
F(2)=1 -> C=2/9.
Будуємо графік щільності розподілу f(x):
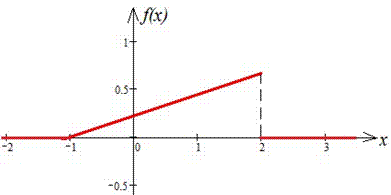та функції розподілу ймовірностей F(x) (при C=2/9)
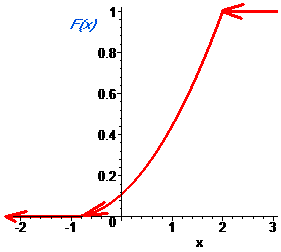Через інтеграл по проміжку обчислюєио математичне сподівання
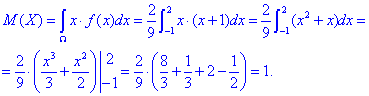
та дисперсію:
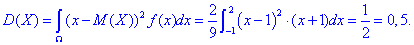
Інтеграли в ймовірності не складні, тому детально їх розписувати не будемо.
Ймовірність того, що в результаті випробувань x набуде значень, що належать інтервалу (a;b) рівна інтегралу:
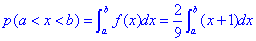
Його значення визначте самостійно.
Завдання 7 Відомі математичне сподівання a=15 та середнє квадратичне відхилення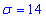 
випадкової величини x, яка розподілена нормально. Обчислити ймовірність того, що
- а) ця випадкова величина прийме значення, які належать інтервалу
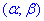=(0;30); - б) абсолютна величина відхилення |x-a|<11 буде менше за
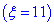
Розв'язання: а) Для знаходження імовірності того, що випадкова величина x прийме значення, які належать інтервалу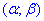 
скористаємось формулою Лапласа:
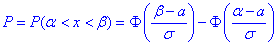
де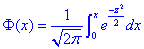 
- інтегральна функція Лапласа (її значення є в таблиці).
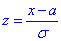- заміна змінних в експоненті.
Отож, знаходимо значення в точках та підставляємо в формулу ймовірності
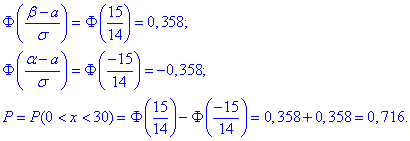
Значення Ф(х) беремо з таблиці, або визначаємо в Maple, Mathematica, MathCad.
б) Для знаходження імовірності того, що абсолютна величина відхилення |x-a|<11 буде менше за 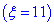скористаємось простою залежністю:
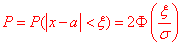Знахоимо єдине значення функції Лапласа
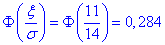
та обчислюємо ймовірність, що абсолютна величина відхилення буде менша 11
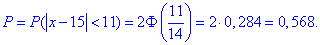
На цьому розв'язування контрольної з теорії ймовірностей завершено. Готові відповіді до контрольних на ймовірності та задач з інших тем шукайте на сторінках сайту.
