Продовжуємо аналізувати готові відповіді із збірника до ЗНО підготовки. Сьогодні розберемо ще кілька завдань на перпендикуляр і похилу у просторі. Пояснення не важкі і можуть бути використані в навчанні як учнями 10-11 класів, так і студентам на перших курсах навчання.
Задача 35.18 Сторони трикутника ABC дорівнюють 10 см, 17 см і 21 см. З вершини найбільшого кута трикутника до його площини проведено перпендикуляр AD, який дорівнює 15 см.
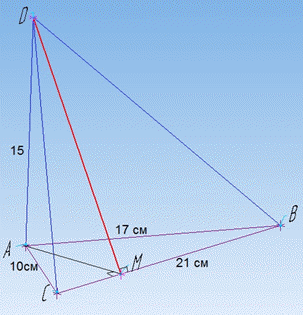
Знайти відстань від точки D до сторони BC трикутника.
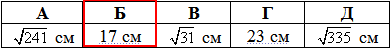
Розв'язання: Маємо трикутник ABC зі сторонами:
AB=17 см, BC=21 см і AC=10 см.
За властивістю трикутника: проти більшої сторони лежить більший кут.
Отже, за умовою, AD⊥(ABC), тому (за властивістю) вона перпендикулярна до кожної прямої, що належить площині ABC (трикутнику ABC).
Відстань від точки D до сторони BC трикутника – перпендикуляр опущений з точки D на пряму BC, тобто DM⊥BC.
Проведемо відрізок AM. Оскільки AD – перпендикуляр до площини ABC, то DM – похила (точка M – основа похилої), а відрізок AM – проекція похилої на площину ABC. Так як DM⊥BC, то за теоремою «про три перпендикуляри» (якщо відрізок, який проведений через основу похилої перпендикулярний до похилої, то він перпендикулярний і до її проекції, і навпаки), тобто AM⊥BC.
Звідси слідує, що AM – висота трикутника ABC, проведена до сторони BC.
Розглянемо трикутник ABC. Знайдемо його півпериметр і площу за формулою Герона (за трьома відомими сторонами):
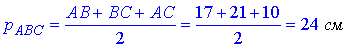– півпериметр ΔABC; 
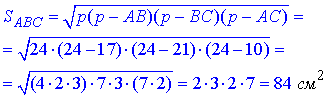– площа ΔABC.
Знайдемо висоту AM трикутника ABC:
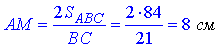
Розглянемо трикутник AMD. Оскільки AD⊥(ABC), то AD⊥AM, тому ΔAMD – прямокутний (∠DAM=90), де AD=15 см – катет і AM=8 см – катет.
За теоремою Піфагора знайдемо довжину відрізка, гіпотенузи DM (відстань від точки K до сторони BC трикутника ABC):
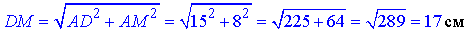
Відповідь: 17 см – Б.
Задача 35.29 Установити відповідність між кутами нахилу (1–4) відрізка завдовжки 10 см до площини та довжиною його проекції на площину (А–Д).
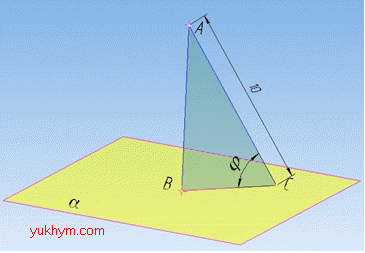
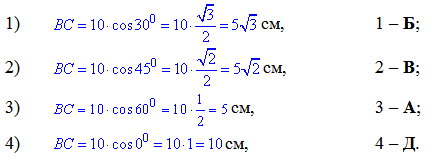
Розв'язання: Маємо площину alpha, точку A, яка не належить площині alpha.
З точки A на площину alpha опущено перпендикуляр AB і похилу AC=10 см . Відрізок BC – проекція похилої AC на площину alpha, тобто AB⊥BC.
Звідси, ∠ACB=phi – кут між відрізком (похилої) AC і площиною alpha. Розглянемо прямокутний трикутник ABC (∠ABC=90), де AC=10 см - гіпотенуза, ∠ACB=phi.
За означенням косинуса прямокутного трикутника знайдемо BC – прилеглий катет до ∠ACB=phi, отже
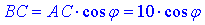
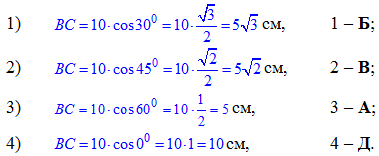
Задача 35.32 З точки A до площини проведено дві похилі AB=30 і AC=40. Знайти відстань від точки A до площини, якщо проекції похилих відносяться як 9:16.
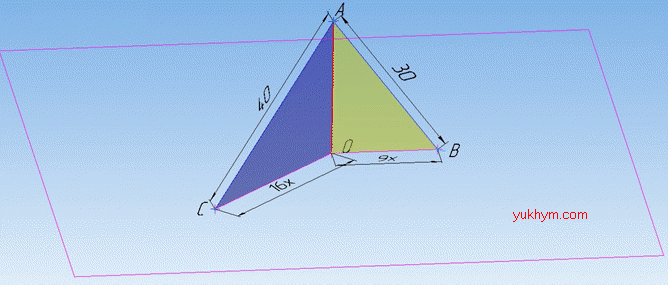
Розв'язання: За умовою задачі маємо AB=30 і AC=40 – похилі, що проведені з точки A до площини hamma. AO – перпендикуляр, опущений з точки A на площину hamma, A0⊥hamma;
BO і CO – проекції похилих AB і AC, відповідно, на площину hamma.
Проекції BO і CO належать площині hamma. Оскільки пряма, яка перпендикулярна до площини, перпендикулярна до кожної прямої, що належить цій площині, то AO⊥BO і AO⊥CO.
За умовою задачі маємо BO:CO=9:16, оскільки більша похила має більшу проекцію, і навпаки, менша похила має меншу проекцію.
Розглянемо трикутники AOB і AOC. Оскільки AO⊥BO і AO⊥CO, то ΔAOB і ΔAOC – прямокутні (∠AOB=90 і ∠AOC=90) зі спільним катетом AO.
Оскільки за умовою задачі BO:CO=9:16, то нехай BO=9x, тоді CO=16x – катети і AB=30 і AC=40 – гіпотенузи ΔAOB і ΔAOC відповідно.
За теоремою Піфагора запишемо рівність для знаходження катета AO:
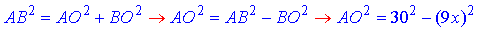
тобто в ΔAOB; (І)
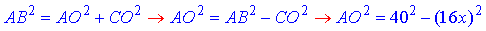
тобто в ΔAOC. (ІІ)
Оскільки перпендикуляр (катет) AO спільний для обох трикутників, то прирівняємо вирази (І) і (ІІ), знайдемо величину x^2:
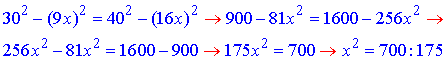
звідси отримаємо x^2=4.
Із виразу (І) знайдемо довжину перпендикуляра AO – відстань від точки A до площини hamma:
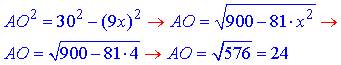
(Не слід розглядати «трикутник» ABC вцілому, як це показано на рис., оскільки це одне з положень двох площин AOB і AOC, які перетинаються по прямій AO. Розглядувані площини можуть перетинатися під будь-яким кутом, і тоді ABC не можна називати Δ, тобто не буде трикутником).
Відповідь: 24.
На цьому готові розв'язки не закінчуються. Ми постійно оновлюємо статті новими цікавими задачами з попередніх етапів ЗНО тестування. Їх Ви легко можете знайти на сторінках сайту.
Якщо маєте подібні приклади, то обов'язково діліться з нами відповідями. В такий спосіб Ви розширете наявну базу готових завдань та допоможете майбутнім поколінням учнів та студентів!
